【终结扩散模型】Consistency Models.OpenAI开源新模型代码,一步成图,1秒18张
【终结扩散模型】Consistency Models.OpenAI开源新模型代码,一步成图,1秒18张
- 0、前言
- Abstract
- 1. Introduction
- 2. Diffusion Models
- 3. Consistency Models
-
- 3.1 Definition
- 3.2 Parameterization
- 3.3 Sampling
- 3.4 Zero-Shot Data Editing
- 4. Training Consistency Models via Distillation
-
- Definition 1.
- Theorem 1.
- 5. Training Consistency Models in Isolation
- 6. Experiments
-
- 6.1. Training Consistency Models
- 6.2. Few-Step Image Generation
-
- Distillation
- Direct Generation
- 6.3. Zero-Shot Image Editing
- 7. Conclusion
- Reference
- 图片结果
代码地址:https://github.com/openai/consistency_models
论文地址:https://arxiv.org/abs/2303.01469
本篇博客详细的介绍了Consistency Models的原理。
值得一提的是这篇文章的第一作者是Yang Song宋飏,之前的score-based generative models即扩散模型也是他写的,这篇文章有很多相关的理论。
0、前言
在 AI 画图的领域,人们一直关注的是扩散模型,人们一直在尝试不断改进,推出了 Stable Diffusion、Midjourney、DALL-E 等技术,并在其基础上构建应用。不过最近,OpenAI 提出的全新生成模型看起来要让这一领域经历一场革命。
作者阵容也非常强大,有本科毕业于清华大学数理基础科学班、目前在 OpenAI 担任研究员的宋飏。宋飏将于 2024 年 1 月加入加州理工学院电子系(Electrical Engineering)和计算数学科学系(Computing and Mathematical Sciences)担任助理教授。此外还包括 OpenAI 联合创始人、首席科学家 Ilya Sutskever。

有网友将其视为扩散模型的有力竞争者!并表示 Consistency Models 无需对抗性训练,这使得它们更容易训练,不容易出现模式崩溃。还有网友认为扩散模型的时代即将结束。更有网友测试了生成速度,3.5 秒生成了 64 张分辨率 256×256 的图片,平均一秒生成 18 张。
首先我们看看 Consistency Model 零样本图像编辑能力:

图 6a 展示了 Consistency Model 可以在测试时对灰度卧室图像进行着色,即使它从未接受过着色任务的训练,可以看出,Consistency Model 的着色效果非常自然,很逼真;图 6b 展示了 Consistency Model 可以从低分辨率输入生成高分辨率图像,Consistency Model 将 32x32 分辨率图像转成 256x256 高分辨率图像,和真值图像(最右边)看起来没什么区别。图 6c 证明了 Consistency Model 可以根据人类要求生成图像(生成了有床和柜子的卧室)。
Consistency Model 图像修复功能:左边是经过掩码的图像,中间是 Consistency Model 修复的图像,最右边是参考图像:

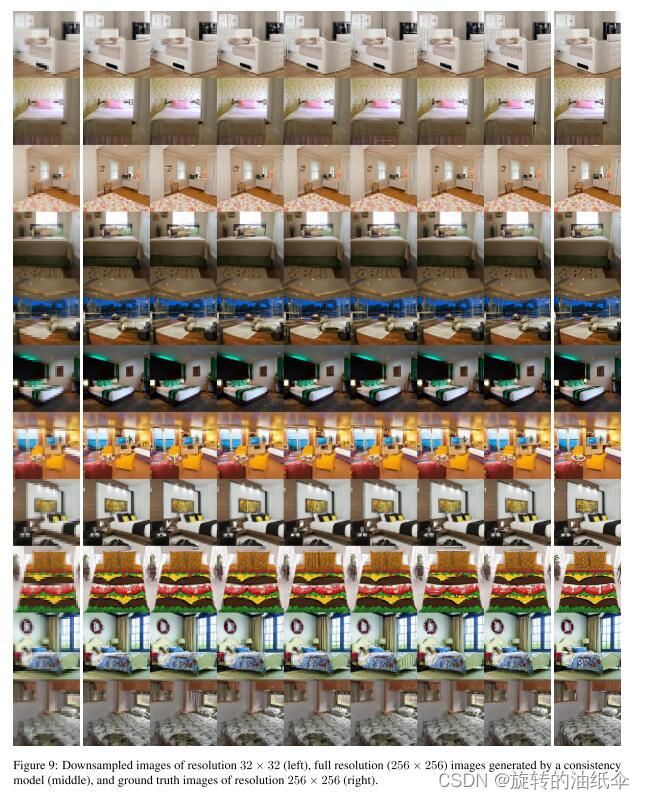
Consistency Model 生成高分辨率图像:左侧为分辨率 32 x 32 的下采样图像、中间为 Consistency Model 生成的 256 x 256 图像,右边为分辨率为 256x 256 的真值图像。相比于初始图像,Consistency Model 生成的图像更清晰。
Abstract
提出问题:扩散模型在图像、音频和视频生成方面取得了重大突破,但它们依赖于迭代生成过程,导致采样速度慢,限制了(caps)它们在实时应用中(real-time applications)的潜力。提出解决方案:为了克服这一局限性,作者团队提出了consistency models,这是一类新的生成模型,它无需对抗性训练就能获得高样本质量。
它们支持设计的快速one-step生成,同时仍然允许用few-step采样,以权衡计算量和样本质量。
它们还支持零样本(zero-shot)数据编辑,如图像修复、着色和超分辨率,而不需要针对这些任务进行具体训练。
consistency models可以用蒸馏预训练扩散模型的方式进行训练,也可以作为独立的(standalone)生成模型进行训练。实验:研究团队通过实验证明了Consistency Models 在one-step 和 few-step 生成中优于现有的扩散模型蒸馏技术。例如,在 one-step 生成方面,Consistency Models在CIFAR10上实现了新的 SOTA FID 3.55,在ImageNet 64x64上实现了6.20的FID。
当作为独立生成模型进行训练时,Consistency Models在CIFAR-10、ImageNet 64x64和LSUN 256x256等标准基准上的表现也优于single-step、非对抗生成模型。
读到目前有可能的疑问是:distill pre-trained diffusion models即什么是蒸馏预训练扩散模型和existing distillation techniques for diffusion models现有的扩散模型蒸馏技术。
蒸馏技术(Luhman&Luhman,2021;Salimans&Ho,2022;Meng et al.,2022;Zheng et al.,2022)是一种用于扩散模型快速采样的方法。最好的蒸馏方法是渐进式蒸馏 (PD, Salimans & Ho (2022)),作者在实验中广泛地将Consistency Models与之比较。
1. Introduction
文章首先介绍了一下Diffusion models,及其优缺点,主要问题就是慢。
关键性技术:
- 能够single-step generation,但是不损失太多样本质量。
- 必要时能够权衡了样本质量与计算量。
- 执行零样本(zero-shot)数据编辑任务的能力。 如image inpainting, colorization, and super-resolution。
Consistency Models 作为一种生成模型,核心设计思想是支持 single-step 生成,同时仍然允许迭代生成,支持零样本(zero-shot)数据编辑,权衡了样本质量与计算量。
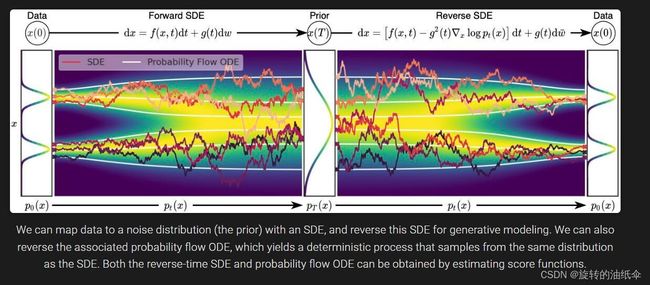
首先 Consistency Models 建立在连续时间扩散模型中的概率流probability flow (PF) 常微分方程ordinary differential equation (ODE) 之上,利用其轨迹trajectories平滑地将数据分布转化为可处理的噪声分布。
如下图 1 所示,给定一个将数据平滑地转换为噪声的 PF ODE,Consistency Models 学会在任何时间步(time step)将任意点(e.g., x t , x t ′ , a n d x T x_t,x_{t\prime},and\ x_T xt,xt′,and xT)映射成轨迹的初始点 x 0 x_0 x0以进行生成式建模。
Consistency Models 一个显著的特性是自洽性(self-consistency):同一轨迹上的点会映射到相同的初始点。这也是模型被命名为 Consistency Models(一致性模型)的原因。

Consistency Models 允许通过仅使用 one network 评估转换随机噪声向量(ODE 轨迹的端点,例如图 1 中的 x T x_T xT)来生成数据样本(ODE 轨迹的初始点,例如图 1 中的 x 0 x_0 x0)。
更重要的是,通过在多个时间步链接 Consistency Models 模型的输出,该方法可以提高样本质量,并以更多计算为代价执行零样本数据编辑,类似于扩散模型的迭代优化。
在训练方面,研究团队为 Consistency Models 提供了两种基于自洽性的方法:
第一种方法依赖于使用数值 ODE 求解器和预训练扩散模型来生成 PF ODE 轨迹上的相邻点对。通过最小化这些点对的模型输出之间的差异,该研究有效地将扩散模型蒸馏为 Consistency Models,从而允许通过 one network 评估生成高质量样本。
第二种方法则是完全消除了对预训练扩散模型的依赖,可独立训练 Consistency Models。这种方法将 Consistency Models 定位为一类独立的生成模型。
值得注意的是,这两种训练方法都不需要对抗训练,并且都允许 Consistency Models 灵活采用神经网络架构。
实验验证:
研究团队证明了Consistency Models在几个具有挑战性的图像基准上的有效性,包括CIFAR-10、ImageNet 64x64和LSUN 256x256。 在经验上,研究团队观察到,作为一种蒸馏方法(distillation approach),Consistency Models在各种数据集和采样步骤数上都优于渐进蒸馏(progressive distillation)。
在CIFAR-10上,Consistency Models达到了一步和两步生成的3.55和2.93的新的SOTA FIDs。 在ImageNet 64x64上,它分别以一次和两次网络评估获得了破纪录的6.20和4.70的FIDs。 当Consistency Models训练为独立的生成模型时,尽管没有利用预训练扩散模型,在单步生成方面还是取得了与渐进蒸馏相当的性能。
它们能够在多个数据集上超越许多GANs,以及所有其他非对抗性的、单步生成模型。 研究团队还表明,Consistency Models可以用于执行零样本数据编辑任务,包括图像去噪、插值、修复、着色、超分辨率和笔画引导的图像编辑。
2. Diffusion Models
一致性模型在很大程度上受到(连续时间)扩散模型理论的启发(Song et al.,2021)。
扩散模型从用随机微分方程(SDE)扩散 P d a t a ( x ) P_{data}(x) Pdata(x)开始
正向过程:
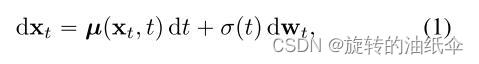
t ∈ [ 0 , T ] t \in [0,T] t∈[0,T],T>0是一个常数。其中 μ ( ⋅ , t ) \mu(⋅,t) μ(⋅,t)称为漂移系数, σ ( t ) 即 g ( t ) \sigma(t)即g(t) σ(t)即g(t)称为扩散系数, w t w_t wt表示标准布朗运动,dw可以看作为无穷小的白噪声infinitesimal white noise。
我们将 x t x_t xt的分布表示为 p t ( x ) p_t(x) pt(x),因此最终样本分布为 p 0 ( x ) ≡ p d a t a ( x ) p_0(x) \equiv p_{data}(x) p0(x)≡pdata(x)
此 SDE 的一个显着特性是存在一个常微分方程 (ODE),被 Song 等人称为概率流 (PF) ODE。 (2021),其在 t 采样的解轨迹根据 p t ( x ) p_t(x) pt(x)分布:
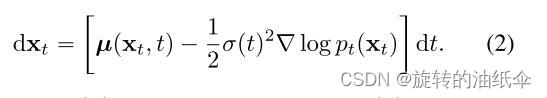
这里 ∇ l o g p t ( x t ) \nabla logp_t(x_t) ∇logpt(xt)是 p t ( x t ) p_t(x_t) pt(xt)的score function,可以训练一个模型 s θ ( x , t ) s_θ(x,t) sθ(x,t)来近似它。所以扩散模型又称为score-based generative models。
公式(1)中的SDE,通常设计使得 p T ( x ) p_T(x) pT(x)接近于一个易于处理的高斯分布 π ( x ) \pi(x) π(x)。 作者沿用Elucidating the Design Space of Diffusion-Based Generative Models的配置,使得 μ ( x , t ) = 0 \mu(x,t)=0 μ(x,t)=0和 σ ( t ) = 2 t \sigma(t)=\sqrt{2t} σ(t)=2t。在这种情况下 p t ( x ) = p d a t a ( x ) ⊗ N ( 0 , t 2 I ) p_t(x)=p_{data}(x) \otimes \mathcal{N}(0,t^2I) pt(x)=pdata(x)⊗N(0,t2I),其中 ⊗ \otimes ⊗表示卷积运算convolution operation,并且 π ( x ) = N ( 0 , T 2 I ) \pi(x) = \mathcal{N}(0,T^2I) π(x)=N(0,T2I)。
对于采样,我们首先通过score matching训练一个分数模型 s ϕ ( x , t ) ≈ ∇ l o g p t ( x ) s_\phi(x,t) \approx \nabla logp_t(x) sϕ(x,t)≈∇logpt(x),然后将其插入等式(2)获得PF ODE的经验估计,其形式为:
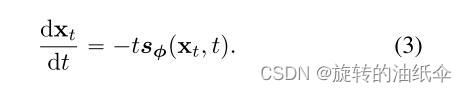
我们称等式(3)为empirical PF ODE.
接下来采样 x ^ T ∼ N ( 0 , T 2 I ) \hat{x}_T \sim \mathcal{N}(0,T^2I) x^T∼N(0,T2I)来初始化empirical PF ODE,并用任一数值ODE求解器,如Euler和Heun Solvers及时向后求解,得到求解轨迹 { x ^ t } t ∈ [ 0 , T ] \{\hat{x}_t\}_{t \in [0,T]} {x^t}t∈[0,T]。
然后,可以将得到的结果 x ^ 0 \hat{x}_0 x^0视为来自数据分布p_{data}(x)的近似样本。
为了避免数值不稳定,通常在 t = ϵ t = \epsilon t=ϵ处停止求解,这里 ϵ \epsilon ϵ是一个固定的小正数,而不是接受 x ^ ϵ \hat{x}_{\epsilon} x^ϵ作为近似样本。 并且follow Karras et al. (2022),我们将图像中的像素值缩小到[-1,1],然后设置T=80”和 ϵ \epsilon ϵ=0.002。
扩散模型因其缓慢的采样速度而成为瓶颈。 显然,使用ODE求解器进行采样需要对得分模型 s ϕ ( x , t ) s_\phi(x,t) sϕ(x,t)进行多次评估,这在计算上是昂贵的。 用于快速采样的现有方法包括更快的数值ODE求解器(Song et al.,2020;Zhang&Chen,2022;Lu et al.,2022;Dockhorn et al.,2022)和蒸馏技术(Luhman&Luhman,2021;Salimans&Ho,2022;Meng et al.,2022;Zheng et al.,2022)。 然而,ODE求解器仍然需要10多个评估步骤才能生成有竞争力的样本。 大多数蒸馏方法像Luhman&Luhman(2021)和Zheng等人。 (2022)依赖于在蒸馏之前从扩散模型收集大量样本数据集,这本身在计算上是昂贵的。 据我们所知,唯一没有这种缺点的蒸馏方法是渐进蒸馏(PD,Salimans&Ho(2022)),我们在实验中将之与consistency models进行了广泛比较。
我们可以使用 SDE 将数据映射到噪声分布(先验),并反转此 SDE 以进行生成建模。我们还可以反转关联的概率流 ODE,这会产生一个确定性过程,该过程从与 SDE 相同的分布中采样。逆时SDE和概率流ODE都可以通过估计得分函数得到。
更多内容参考:score-based generative models。
3. Consistency Models
我们提出了Consistency Models,这是一种新型的生成模型,在设计的核心支持单步生成,同时仍然允许迭代生成零拍数据编辑和样本质量和计算量之间的权衡。 稠度模型可以在蒸馏模式或隔离模式中训练。 在前一种情况下,一致性模型将预先训练的扩散模型的知识提取到一个单步采样器中,显著提高了样本质量的其他提取方法,同时允许零镜头图像编辑应用。 在后一种情况下,一致性模型是孤立训练的,不依赖于预先训练的扩散模型。 这使得它们成为一个独立的新的生成模型类。
下面我们介绍Consistency Models的定义、参数化和采样,并简要讨论它们在零样本数据编辑中的应用。
3.1 Definition
给定公式(2)中PF ODE的解轨迹 { x t } t ∈ [ ϵ , T ] \{x_t\}_{t \in [\epsilon,T]} {xt}t∈[ϵ,T]。我们将consistency function定义为 f : ( x t , t ) ↦ x ϵ \mathbf{f}:(x_t,t)\mapsto x_\epsilon f:(xt,t)↦xϵ。
consistency function具有自洽性的性质:对于属于同一 PF ODE 轨迹的任意 ( x t , t ) (x_t,t) (xt,t)对,其输出是一致的,i.e.,对于所有 t , t ′ ∈ [ ϵ , T ] t,t^\prime \in [\epsilon,T] t,t′∈[ϵ,T]有 f ( x t , t ) = f ( x t ′ , t ′ ) \mathbf{f}(x_t,t)=\mathbf{f}(x_{t^\prime},t^\prime) f(xt,t)=f(xt′,t′)。
对于固定的时间参数, f ( ⋅ , t ) \mathbf{f}(·,t) f(⋅,t)总是一个可逆函数。
如图2所示.consistency model的目标,符号为 f θ \mathbf{f_θ} fθ,是通过学习来加强自洽性属性,从数据中估计这个consistency function f \mathbf{f} f(详见第4节和第5节)。
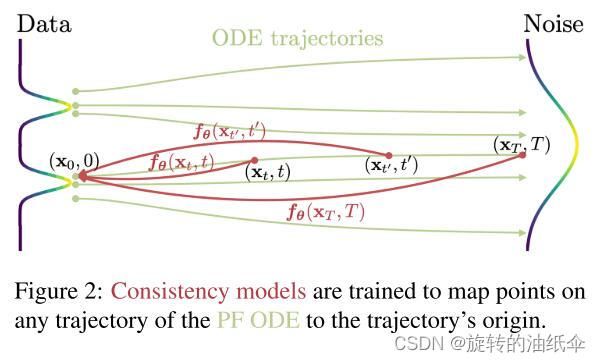
3.2 Parameterization
对于任何consistency function f ( ⋅ , ⋅ ) \mathbf{f}(·,·) f(⋅,⋅),我们有 f ( x ϵ , ϵ ) \mathbf{f}(x_\epsilon,\epsilon) f(xϵ,ϵ),即 f ( ⋅ , ⋅ ) \mathbf{f}(·,·) f(⋅,⋅)是一个恒等式函数。 我们称这种约束为边界条件boundary condition。
一个有效的consistency model必须尊重这个边界条件。 对于基于深度神经网络的consistency model,我们讨论了两种几乎免费almost for free实现该边界条件的方法。
假设我们有一个自由形式的深度神经网络 F θ ( x , t ) F_\theta(x,t) Fθ(x,t),其输出具有与x相同的维数。
第一种方法是简单地将一致性模型参数化为 : 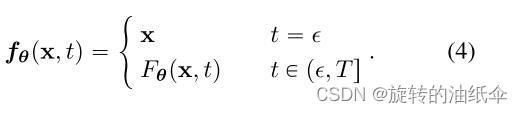
第二种方法是使用skip connections参数化一致性模型,即,: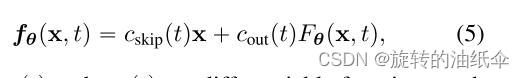
其中 c s k i p ( t ) c_{skip}(t) cskip(t)和 c o u t ( t ) c_{out}(t) cout(t)是可微函数,使得 c s k i p ( ϵ ) = 1 c_{skip}(\epsilon)=1 cskip(ϵ)=1和 c o u t ( ϵ ) = 0 c_{out}(\epsilon)=0 cout(ϵ)=0。 这样,如果 F θ ( x , t ) F_\theta(x,t) Fθ(x,t)和标度系数scaling coefficient是可微的,那么一致性模型在 t = ϵ t=\epsilon t=ϵ处是可微的,这对于训练连续时间一致性模型是至关重要的(附录B.1和B.2)。
公式(5)中的参数化与许多成功的扩散模型(Karras et al.,2022;Balaji et al.,2022)具有很强的相似性,使得更容易借用强大的扩散模型体系结构来构建一致性模型。 因此,我们在所有实验中都遵循第二个参数化。
3.3 Sampling
有了一个训练好了的一致性模型 f θ ( ⋅ , ⋅ ) f_θ(·,·) fθ(⋅,⋅),我们可以通过从初始分布 x ^ T ∼ N ( 0 , T 2 I ) \hat{x}_T \sim \mathcal{N}(0,T^2I) x^T∼N(0,T2I)中采样来生成样本,然后以 x ^ ϵ = f θ ( x ^ T , T ) \hat{x}_\epsilon = f_\theta(\hat{x}_T,T) x^ϵ=fθ(x^T,T)评估一致性模型。
这只涉及一致性模型的一次前向传递,因此在单个步骤中生成样本generates samples in a single step。
重要的是,还可以通过交替去噪和噪声注入步骤alternating denoising and noise injection steps来多次评估一致性模型,以提高样本质量。
在算法1中总结,这种multistep sampling过程提供了用计算量换取样本质量的灵活性。
它在零样本数据编辑中也有重要的应用。
在实践中,我们用贪心算法找到算法1中的时间点time points,其中时间点是一次一个地精确定位pinpointed one at a time 通过三进制搜索ternary search来优化算法1中得到的样本的FID。

3.4 Zero-Shot Data Editing
Consistency models能够在零样本下进行各种数据编辑和操作应用程序;而不需要具体的训练来执行这些任务。
例如,一致性模型定义从高斯噪声向量到数据样本的一对一映射。
与GAN、VAE和归一化流等潜在变量模型类似,一致性模型可以通过遍历潜在空间轻松地在样本之间进行插值(图11)。
由于一致性模型被训练为从任何有噪声的输入 x t x_t xt(其中 t ∈ [ ϵ , T ] t \in [\epsilon,T] t∈[ϵ,T])中恢复 x ϵ x_\epsilon xϵ,因此它们可以针对各种噪声水平执行去噪(图12)。
此外,算法1中的多步生成过程对于通过使用类似于扩散模型的迭代替换过程来求解zero shot中的某些逆问题是有用的。
这使得能够在图像编辑的上下文中实现许多应用,包括修复(图10)、着色(图8)、超分辨率(图6 b)和如在SDEDit(Meng et al., 2021).的笔划引导stroke-guided的图像编辑(图13)。
在第6.3节中,我们以经验证明了一致性模型在许多零样本图像编辑任务中的强大。
图片放在了文末
4. Training Consistency Models via Distillation
我们提出了我们的第一个训练一致性模型的方法,基于蒸馏一个预训练的分数模型 s ϕ ( x , t ) s_\phi(x,t) sϕ(x,t)。
我们的讨论围绕公式(3)中的经验PF ODE展开。通过将分数模型 s ϕ ( x , t ) s_\phi(x,t) sϕ(x,t)插入到PF ODE中得到。
考虑将时间范围 [ ϵ , T ] [\epsilon,T] [ϵ,T]离散成N-1个子区间,边界为 t 1 = ϵ < t 2 < ⋯ < t N = T t_1=\epsilon
 在实际中,是用Karras等人的公式确定的边界,当N足够大时,通过运行一个数值ODE求解器的离散化步骤,我们可以从 x t n + 1 x_{t_{n+1}} xtn+1得到 x t n x_{t_n} xtn的精确估计。
在实际中,是用Karras等人的公式确定的边界,当N足够大时,通过运行一个数值ODE求解器的离散化步骤,我们可以从 x t n + 1 x_{t_{n+1}} xtn+1得到 x t n x_{t_n} xtn的精确估计。
这个估计,我们表示为 x ^ t n Φ \hat{x}^\Phi_{t_n} x^tnΦ,定义如上图公式。
其中: Φ ( … ; ϕ ) \Phi(\dots;\phi ) Φ(…;ϕ)表示应用于经验PF ODE的一步ODE求解器的更新功能。
例如,当使用欧拉求解器时,我们有 Φ ( x , t ; ϕ ) = − t s ϕ ( x , t ) \Phi(x,t;\phi )=-ts_\phi(x,t) Φ(x,t;ϕ)=−tsϕ(x,t)对应于以下更新规则 :
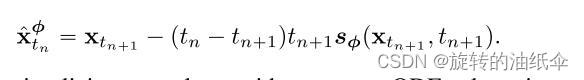
为了简单起见,我们在本工作中只考虑一步ODE求解器。
将我们的框架推广到多步ODE求解器是很简单的,我们把它留在以后的工作中。
由于等式(2)中的PF ODE与SDE(公式1)之间的连接(见第2节),我们可以沿着ODE轨迹的分布进行采样:首先对 x ∼ p d a t a x\sim p_{data} x∼pdata采样,然后将高斯噪声添加到x上。
具体来说,给定一个数据点x,从数据集中采样x,然后从SDE N ( x , t n + 1 2 I ) \mathcal{N}(x,t^2_{n+1}I) N(x,tn+12I)的跃迁密度transition density中采样 x t n + 1 x_{t_{n+1}} xtn+1,然后利用公式(6)数值ODE求解器的一个离散化步骤来计算 x ^ t n Φ \hat{x}^\Phi_{t_n} x^tnΦ,可以有效地生成PF ODE轨迹上的一对相邻数据点 ( x ^ t n Φ , x t n + 1 ) (\hat{x}^\Phi_{t_n},x_{t_{n+1}}) (x^tnΦ,xtn+1)。
也就是说x可以得到 x t n + 1 x_{t_{n+1}} xtn+1,然后 x t n + 1 x_{t_{n+1}} xtn+1可以得到 x ^ t n Φ \hat{x}^\Phi_{t_n} x^tnΦ
即: x ⇒ x t n + 1 ⇒ x ^ t n Φ x \Rightarrow x_{t_{n+1}} \Rightarrow \hat{x}^\Phi_{t_n} x⇒xtn+1⇒x^tnΦ我们要的是 ( x ^ t n Φ , x t n + 1 ) (\hat{x}^\Phi_{t_n},x_{t_{n+1}}) (x^tnΦ,xtn+1)
这激发了我们下面的consistency distillation loss以训练一致性模型。
Definition 1.
consistency distillation loss的定义如下:

其中 θ − \theta^- θ−表示优化过程中过去θ值的运行平均值.
除非另有说明,否则我们在本文中采用定义1中的符号,并用 E [ ⋅ ] \mathbb{E}[·] E[⋅]来表示所有相关随机变量的期望值。
在我们的实验中,我们考虑平方 ℓ 2 \ell_2 ℓ2距离 d ( x , y ) = ∥ x − y ∥ 2 2 d(x,y)=\left \| x-y\right \|_2^2 d(x,y)=∥x−y∥22, ℓ 1 \ell_1 ℓ1距离 d ( x , y ) = ∥ x − y ∥ 1 d(x,y)=\left \| x-y\right \|_1 d(x,y)=∥x−y∥1和学习到的感知图像贴片相似性(LPIPS,Zhang et al.(2018))。
并且发现 λ ( t n ) ≡ 1 \lambda(t_n)\equiv1 λ(tn)≡1在所有的任务和数据集上表现都很好。
在实践中,我们通过对模型参数θ的随机梯度下降来最小化目标,同时用指数移动平均exponential moving average(EMA)更新 θ − \theta^- θ−。 也就是说,给定衰减率为 0 ≤ μ < 1 0\le\mu<1 0≤μ<1,我们在每个优化步骤后执行以下更新:
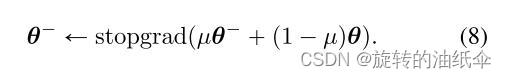
算法2总结了整个训练过程。

根据深度强化学习和基于动量的对比学习中的约定,我们将 f θ − f_{\theta^-} fθ−称为“目标网络”,将 f θ f_{\theta} fθ称为“在线网络”。
我们发现,与简单地设置 θ − = θ \theta^-=\theta θ−=θ相比,==等式(8)中的EMA 更新和”stopgrad“操作符,可以大大稳定训练过程,提高一致性模型的最终性能。 ==
下面我们根据渐近分析asymptotic analysis给出了consistency distillation的理论依据。
Theorem 1.

Proof. 该证明是基于归纳法的,并与数值ODE求解器的全局误差界的经典证明类似(S-Uli&Mayers,2003)。 我们在附录A.2中提供了充分的证明。
由于 θ − \theta^- θ−是θ历史的运行平均值,当算法2的优化收敛时,我们有 θ − = \theta^-= θ−=θ。
也就是说,目标和在线一致性模型最终会相互匹配。 如果一致性模型另外达到零一致性蒸馏损失,则定理1意味着,在某些正则性条件下,只要ODE求解器的步长足够小,估计的一致性模型就可以变得任意精确。 
尽管如此,它们涉及雅可比向量积,并需要前向模式自动微分才能有效实现,这在一些深度学习框架中可能没有得到很好的支持。 我们在定理3到5中提供了这些连续时间蒸馏损失函数,并将细节归入附录B.1。
5. Training Consistency Models in Isolation
一致性模型可以在不依赖于任何预训练扩散模型的情况下进行训练。 这与扩散蒸馏技术不同,使一致性模型成为一类新的独立的生成模型。
在一致性蒸馏中,我们使用一个预训练的分数模型 s ϕ ( x , t ) s_\phi(x,t) sϕ(x,t),来逼近真值分数函数 ∇ l o g p t ( x ) \nabla logp_t(x) ∇logpt(x)。
为了摆脱这种依赖关系,我们需要寻求其他方法来估计得分函数。
实际上,由于以下恒等式(附录A中的引理1)存在着一个对 ∇ l o g p t ( x t ) \nabla logp_t(x_t) ∇logpt(xt)的无偏估计量:

就是用蒙特卡罗估计score function ∇ l o g p t ( x t ) \nabla logp_t(x_t) ∇logpt(xt)
我们现在证明,在 N → ∞ N \rightarrow \infty N→∞的极限内,当使用欧拉方法(或任何高阶方法)作为ODE求解器时,该估计实际上足以取代预训练的扩散模型。
twice continuously differentiable with bounded second derivatives, 二次连续可微的有界二阶导数,
*Proof.*证明基于泰勒级数展开和得分函数的性质(引理1)。 附录A.3提供了完整的证明。

也就是说当 N → ∞ N \rightarrow \infty N→∞且 △ t → 0 \triangle t \rightarrow 0 △t→0时,CT loss占公式(9)主导地位,那么就可以省去后面一项 o ( △ t ) o(\triangle t) o(△t)。
为了提高实际性能,我们建议在训练过程中根据一个调度函数 N ( ⋅ ) N(·) N(⋅)逐步增加N。
其动机(参见,图3D),当N较小时(即ΔT较大),一致性训练损失相对于潜在的一致性蒸馏损失(即方程(9)的等式左边)有较少的“方差variance”,但有较多的“偏差bias”,这有利于在训练开始时更快地收敛。
相反,当N较大时(也就是Δt较小时),它具有较多的“方差”,但较少的“偏差”,这在接近训练结束时是可取的。
为了获得最佳性能,我们还发现,根据调度函数 μ ( ⋅ ) \mu(·) μ(⋅), μ \mu μ应随N变化。 一致性训练的完整算法在算法3中提供,我们实验中使用的调度函数在附录C中给出。



6. Experiments
利用consistency distillation和consistency training来学习真实图像数据集上的consistency models。
实验数据集包括 CIFAR-10 、ImageNet 64x 64 、LSUN Bedroom 256 x 256 、 LSUN Cat 256 x 256。评估指标包括FID,IS,Precision,Recall。
附录C提供了更多的实验细节。
6.1. Training Consistency Models
我们在CIFAR-10上进行了一系列实验,以了解各种超参数对通过一致性蒸馏(CD)和一致性训练(CT)训练的一致性模型性能的影响。
我们首先研究了度量函数 d ( ⋅ , ⋅ ) d(·,·) d(⋅,⋅)、ODE求解器和离散化步骤数N对CD的影响,然后研究了CT中schedule functions N ( ⋅ ) N(·) N(⋅)和 μ ( ⋅ ) \mu(·) μ(⋅)对CT的影响。

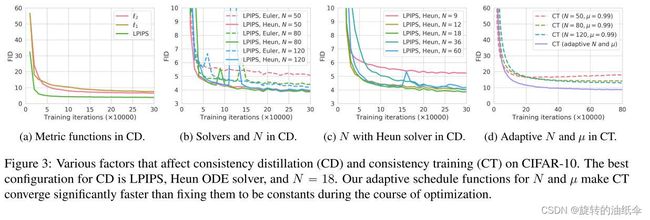
如图3a所示,CD的最优度量是LPIPS,在所有训练迭代中,它的表现都比 ℓ 1 \ell _1 ℓ1和 ℓ 2 \ell _2 ℓ2好得多。这是可以预期的,因为一致性模型的输出是CIFAR-10上的图像,并且LPIPS是专门设计用于测量自然图像之间的相似性的。
接下来,我们研究哪种ODE求解器和哪种离散化步骤N最适合CD。如图3b和3c,Heun ODE求解器和N=18是最佳选择。两者都符合Karras et al.(2022)的建议,尽管我们正在训练一致性模型,而不是扩散模型。
此外,图3b显示出了在相同N的情况下,Heun的二阶求解器一致地优于Euler的一阶求解器。这也证实了Theorem 1,其中定理1指出,由高阶ODE求解器训练的最优一致性模型在相同的N下具有较小的估计误差。
图3c的结果还表明,一旦N足够大,CD的性能变得对N不敏感。鉴于这些见解,除非另有说明,否则我们在下文中使用LPIPS和Heun ODE求解器用于CD。对于CD中的N,我们遵循Karras等人(2022)关于CIFAR-10和ImageNet 64?64的建议。我们在其他数据集上单独调整N(详见附录C)。
由于CD和CT之间的紧密联系,我们在本文中采用LPIPS进行CT实验。
与CD不同,在CT中不需要使用Heun的二阶求解器,因为损失函数不依赖于任何特定的数值ODE求解器。(即与数值求解器相关的是分数网络 s ϕ ( x . t ) s_\phi(x.t) sϕ(x.t)即参数 Φ \Phi Φ)
如图3d所示,CT的收敛对N高度敏感–较小的N导致较快的收敛但较差的样本,而较大的N导致较慢的收敛但在收敛时较好的样本。
这与我们在第5节中的分析相匹配,并促使我们实际选择逐渐增加CT的N和µ,以平衡收敛速度和样本质量之间的权衡。
如图3d所示,N和μ的自适应调度显著提高了CT的收敛速度和采样质量。在我们的实验中,我们针对不同分辨率的图像分别调整调度 N ( ⋅ , ⋅ ) N(·,·) N(⋅,⋅)和 μ ( ⋅ , ⋅ ) \mu(·,·) μ(⋅,⋅),更多细节见附录C。
6.2. Few-Step Image Generation
Distillation
在当前文献中,与我们的一致性蒸馏(CD)最直接可比的方法是渐进蒸馏(PD,Salimans & Ho(2022));迄今为止,这两种方法都是在蒸馏之前不构建合成数据的do not construct synthetic data before distillation 唯一蒸馏方法。
与此形成鲜明对比的是,其他蒸馏技术,如知识蒸馏(Luhman & Luhman,2021)和DFNO(Zheng等人,2022),必须通过用昂贵的数值ODE求解器从扩散模型生成大量样本来准备大的合成数据集。
我们在CIFAR-10、ImageNet 64x64和LSUN 256x256上对PD和CD进行了全面的比较,所有结果都在图4中报告。
所有方法均从内部预训练的EDM(Karras等人,2022)模型中蒸馏。All methods distill from an EDM (Karras et al., 2022) model that we pre-trained in-house.
我们注意到,在所有采样迭代中,与Salimans & Ho(2022)的原始论文中的平方 ℓ 2 \ell_2 ℓ2距离相比,使用LPIPS度量均匀地改善了PD。using the LPIPS metric uniformly improves PD compared to the squared 2 distance in the original paper ofSalimans & Ho (2022).
PD和CD都随着我们采取更多的采样步骤而改善。
我们发现CD在所有数据集,采样步骤和度量函数中均优于PD,除了Bedroom 256x256上的单步生成,其中CD用 ℓ 2 \ell_2 ℓ2的性能略低于PD用 ℓ 2 \ell_2 ℓ2。
如表1所示,CD甚至优于需要合成数据集构建的蒸馏方法,例如知识蒸馏(Luhman & Luhman,2021)和DFNO(Zheng et al.2022年)。

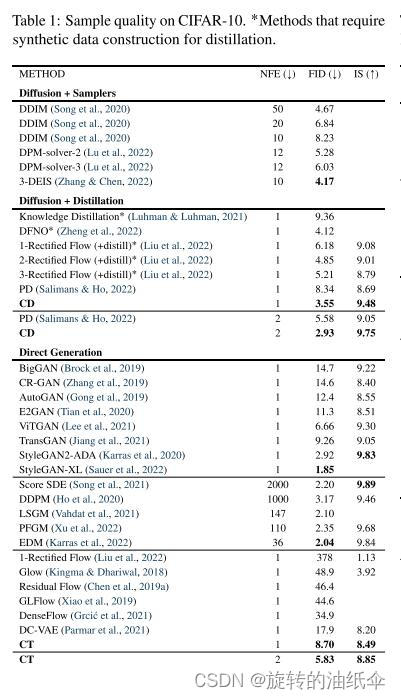
可见CT一步与很少步的生成能力的强大。表 1 表明,CD( consistency distillation )优于 Knowledge Distillation、DFNO 等方法。
Direct Generation
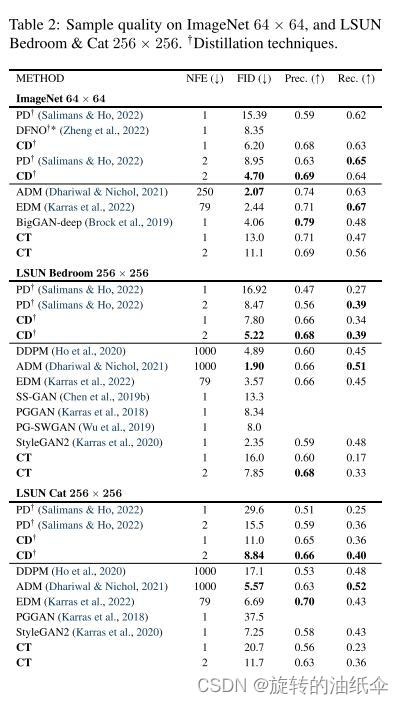
在表1和表2中,我们将一致性训练(CT)的样本质量与使用一步和两步生成的其他生成模型进行了比较。
我们还包括PD和CD结果以供参考。两个表都报告了从 ℓ 2 \ell_2 ℓ2度量函数获得的PD结果,因为这是Salimans & Ho(2022)原始论文中使用的默认设置。
为了公平比较,我们训练PD和CD来提取distill相同的EDM模型。
在表1和表2中,我们观察到CT优于所有单步、非对抗性生成模型,即VAE和归一化流,在CIFAR-10上有显著性差异。(但是没有GAN好。)
此外,CT获得了与PD相当的质量,用于单步生成而不依赖于蒸馏。
在图5中,我们提供了EDM样本(顶部)、单步CT样本(中间)和两步CT样本(底部)。
在附录E中,我们在图14到21中显示了CD和CT的额外样本。
重要的是,从相同的初始噪声向量获得的所有样本具有显著的结构相似性,即使CT和EDM模型彼此独立地训练。这表明CT不太可能遭受模式崩溃,因为EDM不会。(其中EDM (Karras et al., 2022))

6.3. Zero-Shot Image Editing
与扩散模型相似,一致性模型通过修改算法1中的多步采样过程来允许零样本图像编辑。
我们使用一致性蒸馏在LSUN卧室数据集上训练的一致性模型证明了这种能力。
在图 6a中,我们证明了这种一致性模型可以在测试时对灰度卧室图像进行着色,尽管它从未被训练过着色任务。
在图 6b,我们证明了相同的一致性模型可以从低分辨率的输入生成高分辨率的图像。
在图 6C,我们还证明了它可以根据人类创建的笔画输入生成图像,就像SDEdit用于扩散模型(Meng et al.,2021)。
同样,这种编辑能力是零样本zero-shot,的,因为模型没有根据笔画输入进行训练。
在附录D中,我们还演示了一致性模型在修复(图10)、插值(图11)和去噪(图12)方面的零样本能力,并提供了更多关于着色(图8)超分辨率(图9)和笔画引导图像生成(图13)的示例。
7. Conclusion
我们介绍了一致性模型,这是一种专门设计用于支持一步或几步生成的生成模型。
我们的经验证明,我们的一致性蒸馏方法在许多图像基准和各种采样迭代上优于现有的扩散模型蒸馏技术。
此外,作为一个独立的生成模型,一致性模型优于其他允许单步生成的可用模型,不包括GANs。
与扩散模型类似,它们还允许零样本图像编辑应用,如修补、着色、超分辨率、去噪、插值和笔画引导图像生成。
此外,一致性模型与其他领域中使用的技术有着惊人的相似之处,包括深度Q学习(Mnih et al.,2015)和基于动量的对比学习(Grill et al.,2020;He et al.,2020)。 这为这些不同领域的思想和方法的交叉研究提供了令人兴奋的前景。
了解更多内容,请参考原论文。
Reference
【1】:终结扩散模型:OpenAI开源新模型代码,一步成图,1秒18张
图片结果
spherical linear interpolation. 球面线性插值。