BFGS算法_python

---

程序

代码如下（示例）：

# 创作者：眰恦
# 地  点：桂林
# 时  间：2021/11/5  21:40

import math
import numpy as np
import matplotlib.pyplot as plt

def fun(x):
    return np.array([100*(x[0]**2 - x[1])**2 +(x[0] - 1)**2])

def gfun(x):
    return np.array([400*x[0]*(x[0]**2-x[1])+2*(x[0]-1),-200*(x[0]**2-x[1])])

def hess(x):
    return np.array([[1200*x[0]**2-400*x[1]+2,-400*x[0]],[-400*x[0],200]])

def BFGS(fun,gfun,hess,x0):
    maxk = 5000
    rho = 0.55
    sigma = 0.4
    epsilon = 1e-5
    k = 0
    W = np.zeros((2, 10 ** 3))
    n = np.shape(x0)[0]
    Bk = np.eye(n) # 初始对称正定矩阵，Bk=np.linalg.inv(hess(x0))
    W[:, 0] = x0

    while k < maxk:
        gk = gfun(x0)
        if np.linalg.norm(gk) < epsilon:
            break
        dk = -1.0*np.linalg.solve(Bk,gk)
        m = 0
        mk = 0

        while m < 20:
            if fun(x0+rho**m*dk) < fun(x0) + sigma*rho**m*np.dot(gk,dk):
                mk = m
                break
            m += 1
        W[:,k] = x0
        # BFGS校正
        x = x0+rho**mk*dk
        sk = x-x0
        yk = gfun(x)-gk
        if np.dot(sk,yk) > 0:   # yk'*sk>0
            Bs = np.dot(Bk,sk)
            # print('-'*10)
            # print(Bs)   [-0.01057562  0.00546504]
            # print(Bs.reshape((n,1)))    [-0.01057562 ; 0.00546504]
            # print('*'*10)
            ys = np.dot(yk,sk)
            sBs = np.dot(np.dot(sk,Bk),sk)

            Bk = Bk-1.0*Bs.reshape((n,1))*Bs/sBs+1.0*yk.reshape((n,1))*yk/ys
        k += 1
        x0 = x
    W = W[:,0:k]  # 记录迭代点
    return x0,fun(x0),k,W
    # return W

X0 = np.arange(-1.5,1.5-0.05,0.05)
X1 = np.arange(-3.5,2+0.05,0.05)
[x0,x1] = np.meshgrid(X0,X1)
f=100*(x1-x0**2)**2+(1-x0)**2 # 给定的函数
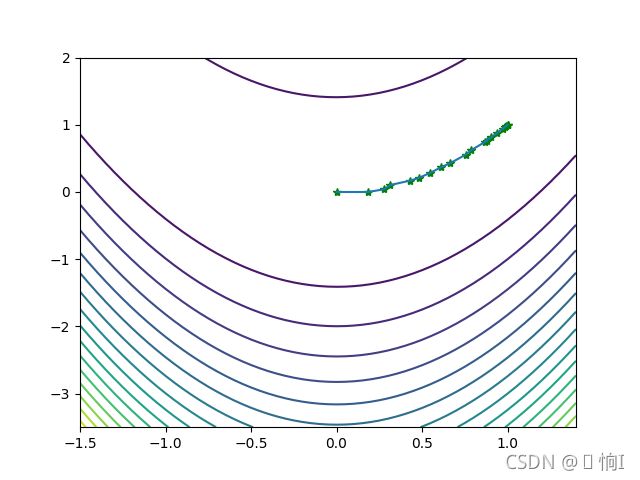
plt.contour(x0,x1,f,20)


x0,fun0,k,W=BFGS(fun,gfun,hess,np.array([0,0]))  # 此处x0是行向量，计算时要转成列向量
print(x0,fun0,k)

# x0 = np.array([0,0])
# W = BFGS(x0)
plt.plot(W[0,:],W[1,:],'g*',W[0,:],W[1,:])  # 画出迭代点轨迹
plt.show()

---

总结

[0.99999532 0.99999061] [2.20047705e-11] 20