C++算法初级6——排序2（快速、归并、计数排序）

C++算法初级6——排序2

快速排序

基本思想：

1. 快速排序是一种基于分治法的排序。其基本思想在于固定一个分界线，将整个序列按照小于分界线和大于分界线划分，然后再分别对划分好的子段进行排序。
2. 快速排序的时间复杂度在理想情况下是O(nlogn)，但如果选取分界线每次都是子段中的最大值或最小值的话，时间复杂度可能会退化到O(n ² )。在内存使用上，因为整个移动过程都在原数组中进行的，所以属于原地排序。
3. sort函数是C++标准模板库（STL）中一种对快速排序的优化实现，可以通过传入头指针、尾指针和比较函数来对数组中的对象进行排序。
   代码实现：

#include 
using namespace std;
int a[10] = {2, 3, 1, 5, 4};
int n = 5;
int main() {
    sort(a, a + n);  //sort函数的两个参数，头指针和尾指针
    for (int i = 0; i < n; ++i) cout << a[i] << ' ';
    cout << endl;
}

在此，我们详细描述一下给任意n个数排序的快速排序算法：

假设我们要对数组a[1…n]排序。初始化区间[1…n]。

令l和r分别为当前区间的左右端点。下面假设我们对l到r子段内的数字进行划分。取pivot = a[l]为分界线，将pivot的数字移到右边，然后将pivot放在中间。假设pivot的位置是k。

如果左边区间[l…k-1]长度大于1，则对于新的区间[l…k-1]，重复调用上面的过程。

如果右边区间[k+1…r]长度大于1，则设置新的区间[k+1, r]，重复调用上面的过程。

当整个过程结束以后，整个序列排序完毕

代码实现，不调用sort

void quickSort(int a[],int left, int right)
{
    if(left>=right) return; 

    int pivot = a[left];
    int pi = left;
    int pj = right;
    
    while(pi<pj)
    {
        while(a[pj]>=pivot&&pi<pj) //要先找右边的，先找左边逻辑不对，举例3571861
        {
            pj--;
        }
        
        while(pi<pj&&a[pi]<=pivot)
        {
            pi++;
        }

        if(pi!=pj)
        {
            swap(a[pi],a[pj]);
        }
    }

    swap(a[left],a[pj]);
    quickSort(a,left,pi-1);
    quickSort(a,pi+1,right);

    if(left==0&&right==9)
    {
        for(int i=0;i<10;i++)
        {
            cout<<a[i]<<" ";
        }
    }
}

归并排序

基本思想

1. 和快速排序一样，归并排序也是基于分治法的排序算法。其基本思想在于将待排序序列分成长度相差不超过1的两份，分别对左右子段进行同样的划分和排序过程，最后将两个已经排好序的子段合并成整个完整的有序序列。
2. 归并排序的时间复杂度是O(nlogn)，在实现时，需要辅助数组帮助合并子段，所以是一种非原地排序算法。
3. 和快速排序不同的是，归并排序是一种稳定排序，即相同元素在排序前后的数组中相对位置不变。
4. stable_sort函数是C++标准模板库（STL）中一种对归并排序的优化实现，可以通过传入头指针、尾指针和比较函数来对数组中的对象进行排序。

代码

#include 
using namespace std;
int a[10] = {0, 2, 3, 1, 5, 4}; // 1-base，0号元素无意义
int n = 5;
bool cmp(int x, int y) {        // 比较函数，函数的参数是当前比较的两个数组中的元素
    return x > y;               // x和y分别为排序数组中的两个元素。
}                               // 当函数返回值为true时，x应该排在y的前面。
int main() {
    stable_sort(a + 1, a + n + 1, cmp);    // 比较函数作为第三个参数传入sort函数
    for (int i = 1; i <= n; ++i) cout << a[i] << ' ';
    cout << endl;
}

手写版代码：

void mergeSort(int a[],int left,int right)
{
    if(left>=right) return;
    int mid = (left+right)>>1;
    mergeSort(a,left,mid);
    mergeSort(a,mid+1,right);
    merge(a,left,mid,right);

    if(left==0&&right==9)
    {
        for(int i=0;i<10;i++)
        {
            cout<<a[i]<<" ";
        }
    }
}

在归并操作的时候，我们使用一个辅助数组b，先把待合并的部分整个复制到b数组里，如下图：

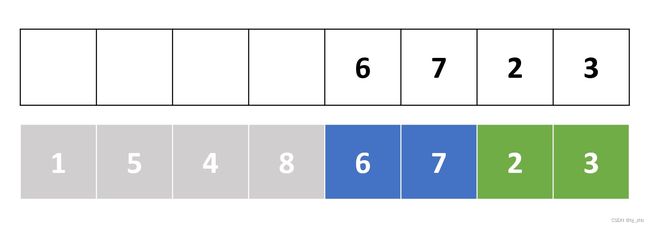
然后，我们用k枚举原序列中l到r的位置，依次从b数组中挑选元素填入当前位置k中。我们维护两个指针i，j，分别指向两个子段的最小元素。如果：

j已经移出子段的末尾；
或者i和j都仍然指向子段中的元素，但i指向的元素比j指向的元素小；
那么我们将i指向的元素填到k的位置，并且将i后移。否则，就将j指向的元素填写到k的位置。

void merge(int a[],int left,int mid,int right)
{
    int temp[100];   
    for(int i=left;i<=right;i++)
    {
        temp[i] = a[i]; // 将a数组对应位置复制进辅助数组
    }

    int pi=left;
    int pj=mid+1;

    for(int k=left;k<=right;k++)
    {
        // 如果：1. ``j``已经移出子段的末尾；        
        // 2. 或者``i``和``j``都仍然指向子段中的元素，但``i``指向的元素比``j``指向的元素小；
        if(pj>right || (pi<=mid && temp[pi]<=temp[pj]))
        {
            a[k] = temp[pi++];
        }
        else
        {
            a[k] = temp[pj++];
        }
    }
}

计数排序

基本思想
如果给出下面100个数字，要求用肉眼给它们排序。

17, 88, 21, 73, 80, 10, 71, 73, 40, 50
98, 3, 100, 82, 71, 86, 65, 2, 68, 23
81, 6, 43, 35, 3, 75, 14, 81, 12, 34
90, 10, 12, 42, 88, 61, 61, 72, 43, 23
41, 71, 31, 13, 63, 72, 72, 18, 50, 32
82, 21, 97, 62, 28, 2, 78, 88, 77, 29
10, 44, 70, 59, 79, 55, 31, 96, 1, 47
32, 20, 70, 18, 79, 87, 80, 59, 58, 13
47, 55, 23, 12, 38, 7, 92, 5, 82, 97
91, 90, 29, 16, 66, 42, 18, 77, 16, 42
这一定是个比较困难的问题。

但如果这100个数字长成下面这个样子：

1, 0, 1, 0, 1, 0, 1, 1, 1, 0
1, 0, 1, 0, 1, 0, 1, 0, 1, 0
0, 0, 0, 0, 1, 1, 0, 1, 0, 0
1, 0, 0, 1, 0, 1, 0, 1, 1, 0
0, 0, 1, 0, 1, 0, 1, 0, 1, 1
1, 0, 1, 1, 1, 1, 0, 1, 0, 1
1, 0, 1, 0, 0, 1, 0, 0, 0, 1
1, 1, 1, 0, 0, 1, 0, 1, 1, 0
0, 0, 0, 1, 1, 1, 0, 1, 0, 1
1, 1, 1, 0, 0, 1, 0, 0, 1, 1
我们会发现这100个数字只有0和1两种情况，而假设要求将该序列从小到大排序，那么序列中的0一定会出现在1的前面。所以我们只需要统计0的个数和1的个数（假设有a个0和b个1），在写答案时，先写a个0，再写b个1即可。

上面的例子体现了计数排序的基本思想：

假设我们已知在待排序的序列中，值都是整数并且出现在一个很小的范围内，例如[0…1000]。那么，我们可以通过：

1. 分别统计每一种可能的值在序列中出现的次数。
2. 从小到大（假设要求将序列从小到大排序）枚举所有值，按照出现次数输出对应个数。
   来完成排序过程。

计数排序算法描述
给定长度为n的序列，假设已知序列元素的范围都是[0…K]中的整数，并且K的范围比较小（例如

10⁶ ，开长度为10⁶ 左右的int类型数组所占用的内存空间只有不到4M）。解决该问题的计数排序算法描述如下：

1. 使用整数数组cnt统计[1…K]范围内所有数字在序列中出现的个数。
2. 使用变量i枚举1到K，如果i出现了cnt[i]次，那么在答案序列的末尾添加cnt[i]个i。

下图是一个n=6, K=3的例子：

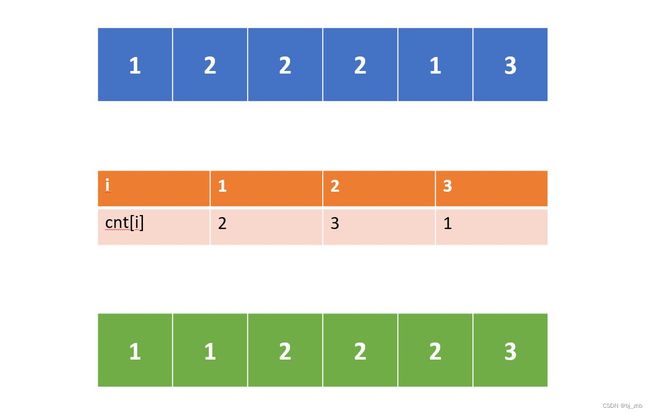
值得一提的是，如果元素的范围可以被很容易转换到[0…K]，我们也可以使用计数排序。如果元素范围是[A…B]，我们可以通过简单的平移关系将其对应到[0…B-A]上。或者所有数值均为绝对值不超过100的两位小数，那么我们可以通过将所有数字放大100倍将其转换为整数。

找出原序列中元素在答案中的位置
在有些场景中，比如我们根据(key, value)中的key关键字进行排序，如果只是使用上面的计数排序，我们无法将value放到相应的key在答案序列中的对应位置中。但是，如果我们可以将原序列和答案序列元素的位置对应求出来，那么这个问题就能得到解决。

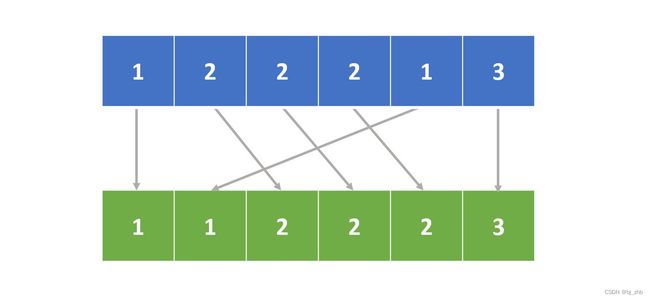
试想，对于原序列中的数字x，它排序后的位置可能出现在哪里呢？
因为在排序后的序列中，假设
x第一次出现的位置是i，最后一次出现的位置是j，那么i之前的元素一定比x小，j出现的位置之后的元素一定比x大。假设原序列小于x的个数是A，小于等于x元素个数是B，
x可能出现的位置一定是[(A+1)…B]！

sum数组的求法和意义

那么，我们怎样求出A和B呢？假设我们对cnt数组求前缀和，如下图所示，cnt数组元素求前缀和后为sum数组：

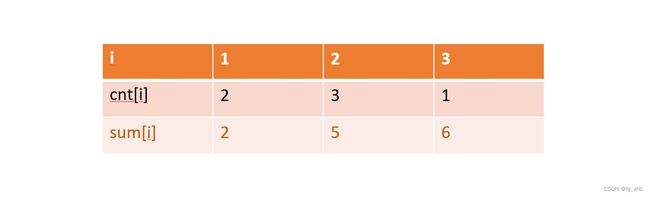
这里，我们指出sum数组的意义：对于一个序列中可能出现的值x，sum[x]的含义是“小于等于x的数字个数”，同时，也可以看作指向答案序列中最后一个x出现的位置的指针。

利用sum数组分配位置

所以对于值x，A即为sum[x - 1]，B 即为sum[x]，x出现的排名为$[(sum[x-1]+1)..sum[x]]$，等价于[(sum[x] - cnt[x] + 1)…sum[x]]。我们将sum数组的位置标出来：

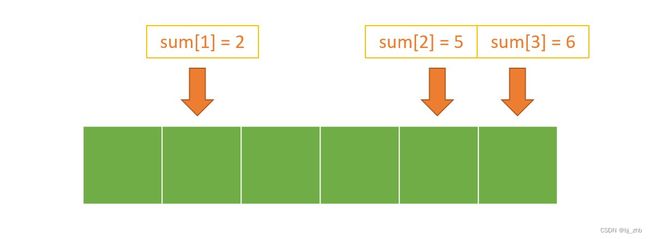
然后我们从后往前扫描每个元素，把它填到当前的sum对应值指向的格子中，并把sum向前移动。如下图：

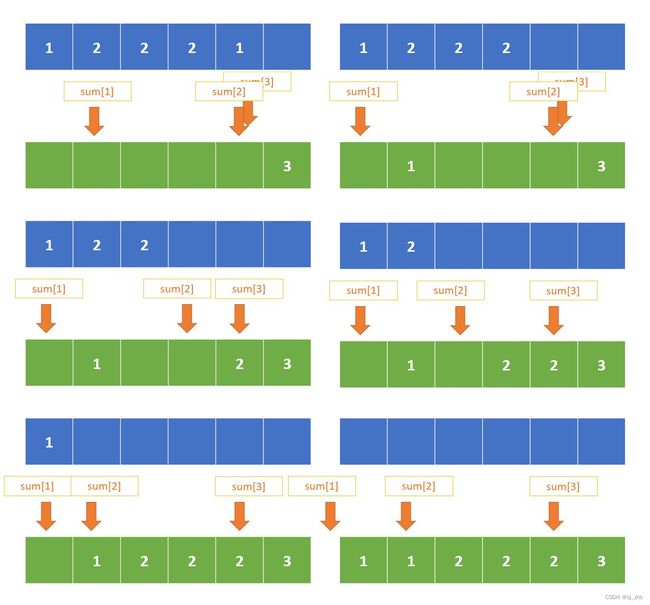
有了原序列和答案序列的位置对应，我们也可以据此将对应元素放入答案数组中。所以该版本的计数排序算法描述如下：

1. 统计原序列中每个值的出现次数，记为cnt数组。
2. 从小到大枚举值的范围，对cnt数组求前缀和，记为sum数组。
3. 从后往前枚举每个元素a[i]，分配其在答案中的位置idx[i]为当前的sum[a[i]]，也就是将其放在所有值等于a[i]中的最后一个。并且将sum[a[i]]减少1，保证下次再遍历到同样的值时，它分配的位置正好在idx[i]前面一个。

#include 
#define N 1000005
#define K 1000001    // 假设非负整数最大元素范围为1000000
using namespace std;
int a[N], n, b[N];
int cnt[K];
int main() {
    // 输入
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        ++cnt[a[i]];    // 这里通过计数数组cnt来维护每一种值出现的次数
    }
    
    // 维护最终有序序列
    for (int i = 0, j = 0; i < K; ++i)      // 枚举每一种值i，指针j用来枚举填充答案数组中的位置
        for (int k = 1; k <= cnt[i]; ++k)   // 根据该值出现的次数
            b[++j] = i;                     // 添加对应个数的i到答案序列
	
    // 输出
    for (int i = 1; i <= n; ++i)
        cout << b[i] << ' ';
    cout << endl;
    
    return 0;
}

上述计数排序实现方法的时间和空间复杂度都是O(n+K)。正因为它不是基于比较的排序，所以才能达到比O(nlogn)更好的时间复杂度。
因为在上面的代码中一共开了3个数组，长度分别为O(N)（对于a和b）和O(K)（对于cnt）。整个空间复杂度为O(N + K)。

计数排序的基本思想还可以拓展成桶排序和基数排序。使用桶排序和基数排序的，可以对更大范围内的，甚至不是整数的序列进行排序。

找出原序列中的元素和答案数组中的对应

• 在输入部分，我们统计每一种值出现的次数
• 在求原序列和答案序列的位置对应关系的部分，我们对cnt数组求前缀和，并存储在sum中。回忆上一节提到，对于一个值x，sum[x]的含义是“小于等于x的数字个数”，同时，也可以看作指向答案序列中最后一个x出现的位置的指针。
• 然后，我们从后向前枚举原序列的每个元素x，将sum[x]指向的位置分配给它，存在idx数组中，然后将sum[x]前移。这里“从后向前”是因为考虑到对于同一个值，分配位置的顺序是从后向前。所以，我们从后向前枚举原序列，可以保证在值相同的情况下，在原序列中出现在后面的元素会被分配到更大的位置，也就保证列排序的稳定性。
• 因为原序列中i位置的数字，在答案序列中出现在idx[i]处。所以我们据此生成答案序列。

代码

#include 
#define N 1000005
#define K 1000001    // 假设非负整数最大元素范围为1000000
using namespace std;
int a[N], n, b[N];
int cnt[K], sum[K];
int idx[N];    // 用来记录原序列中每个元素在新序列中的位置
int main()
{
	cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        ++cnt[a[i]];    // 这里通过计数数组cnt来维护每一种值出现的次数
    }
    //计算cnt数组的前缀和
    sum[0] = cnt[0];               // 假设最小值为0
    for(int i=1;i<K;i++)
    {
    	sum[i]=sum[i-1]+cnt[i];
    }
    //给每个元素分配位置
    for(int i=n;i>0;i--) //从后向前枚举
    {
    	idx[i]=sum[a[i]];
    	sum[a[i]--;
    }
    
    //把最终的结果放到b数组中
    for(int i=1;i<K;i++)
    {
    	b[idx[i]] = a[i]; //idx[i] is a[i]'s index in array b
    }
    // 输出
    for (int i = 0; i <= n; ++i)
        cout << b[i] << ' ';
    cout << endl;
    
    return 0;
}