2023CSP-CCF前三题 田地丈量、垦田计划、LDAP解题分析
文章目录
- CCF考试系统传送门
- 前言(吐槽,可跳过)
- 一、田地丈量
-
- 1.题目内容
- 2.题意简述
- 3.题解分析
- 4.完整代码
- 二、垦田计划
-
- 1.题目内容
- 2.题意简述
- 3.题解分析
- 4.完整代码
- 三、LDAP
-
- 1.题目内容
- 2.题意简述
- 3.题解分析
- 4.完整代码
CCF考试系统传送门
2023.03第29次CCF-CSP计算机认证考试
CCF计算机软件能力认证考试系统
前言(吐槽,可跳过)
大二菜鸟第一次参加CSP考试,发挥得很烂(其实是实力太菜了 ),考前也没看往年题目套路,有很多不甘吧,不过拟打算六月再参加一次。如果早知道题目难度是依次递增的,就不写完两题就去啃最后一题了,最后写第三题的时候都在赶,最后一题还没啃下多少分…
话不多说,接下来分享我的思路。
一、田地丈量
1.题目内容
2.题意简述
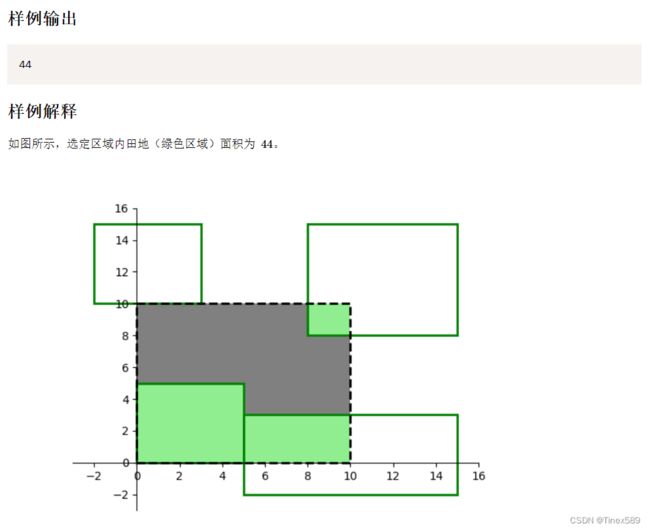
在坐标轴上给定你一个矩形,再给若干个矩形(这些矩形之间无重合部分),算出这些矩形与你的矩形的重合部分面积总和为多少。
3.题解分析
枚举出矩形在不同情况下的不同计算方法,如在边上、被包含的情况等等,时间复杂度为O(n)。这种方法的好处在于几乎不用思考用什么算法,只需要注意边界条件。
不得不感谢出题人手下留情,给出了不会出现矩形多次覆盖同一区域的情况的条件,否则情况将会复杂一点。
思路图解:

补充:求重叠线段长度从而算出重叠面积的方法更为简便。
4.完整代码
#include二、垦田计划
1.题目内容
2.题意简述
有几块田,耕完需要的时间都不同,花的资源也不同,但是所有田可以同时耕。用资源能缩短耕田的天数,但是最少不能小于k天。需要思考如何分配资源使总天数最少。
3.题解分析
听一些大佬说是二分题。但是我没有这样做,提供一下我当时的思路。
这题让我想起木桶盛水的故事,“由长短不一的木板造出的木桶能盛多少水取决于最短的那块木板”。不过这题是反过来的,花费的总时间取决于最多天数的田,最多天数的田不变的情况下,就算分配所有资源给后面的田,需要的总时间也不变。于是我们考虑贪心法:每次分配资源给最大天数的田。
接下来,还需要考虑一个问题。如果存在若干个天数相同的田,只减少其中若干片田的时间,总时间仍不变。就是说,要使这种情况下的天数有效减少,必须同时削减所有相同天数的田,而且需要减少相同时间,使它们步伐保持一致,所以我们可以考虑合并方法,把所有具有相同天数的田所需的资源合并在一起,视为一块田。同时,在计算中削减某块田的天数后也要进行合并。
基于此,我想到了使用STL库的map。将键值对设置为<天数,所需资源>,方便将相同的天数合并它们的资源。另外,map具有自动对key进行排序的特点,正好满足我们对天数进行贪心的需求。需要注意map默认对key降序排列,所以要加greater。
map<ll,ll,greater<ll>>land;//按天数降序
在map的begin位置的是天数最大的田,要做的是将它与天数第二大的田合并资源,合并后,删除该键值对。循环执行,直到资源不够了或者所有天数都为k时结束。
m-=cost;
it1->second+=it->second;
land.erase(it->first);
还有一种情况,资源不够合并了。这时算算当前资源还能减多少天,算出来直接输出,程序结束。
ans=it->first;
while(m>=it->second)
{
m-=it->second;
ans--;
}
printf("%lld",ans);
break;
需要注意,无论是否存在天数为k的田,都需要加入key为k的键值对,以保证每次都能取出两个键值对进行合并。
land[k]+=0;//最少天数,保证每次能有两个合并
时间复杂度分析:需要分两种情况:
1.所有都能减少到k天,外层循环为O(n),即总共扫过一遍表;map.erase操作复杂度为O(logn),总共为O(nlogn)。
2.资源不够,设当前位置田在原来排第m位,则已进行mlogm次运算,内层循环不超过1e5-k次,复杂度为O(mlogm+1e5-k)。
由于m<=n,所以两种情况复杂度相差不大。
可以优化: 在每次合并操作之后让迭代器往后移一位(注意跳出循环条件和迭代器赋值需要些许改动),省去了erase,复杂度为O(n)。不过这题数据量不大,O(nlogn)和O(n)都行(map重度依赖 )。
补充:又回来补了个二分法,就当练手
这题的二分主要坑点在于多数情况下是不能直接搜到答案的(资源不能恰好分完),而是直接循环到low<=high,最后停止处落在答案左侧或右侧,但一定经过答案。另外,从最小天数k到田的最大天数都是我们的搜索范围,low应该初始化为k。
对于如何找到答案,我们每次得到预测天数mid时,计算大于mid天的田全部减到mid天需要多少资源,此时有三种情况,我们用不同的返回值:
0——刚好用完,直接得出答案;
-1——资源不够;
1——资源盈余。
用这样的函数实现:
int dcs(int day)
{
int sum=0;
for(int i=n-1;land[i].first>day&&i>=0;i--)
sum+=land[i].second*(land[i].first-day);
if(m==sum) return 0;//资源刚好
else if(m<sum) return -1;//不够资源
else return 1;//资源盈余
}
在二分查找中调用这个函数,同时对返回值进行处理。最终答案如果不能恰好分配,那答案一定是在资源有盈余的情况下得出来的,所以我们用最小天数mind维护返回值为1的情况,查找结束后mind即为答案。
while(low<=high)
{
mid=(low+high)>>1;
if(dcs(mid)==0) break;
else if(dcs(mid)==1) {mind=min(mind,mid);high=mid-1;}
else low=mid+1;
}
return mind;
4.完整代码
贪心:
#include二分:
#include三、LDAP
1.题目内容
2.题意简述
给定用户的编号和他们各自的属性名称和属性值,再给出满足题目规定的表达式的用户:
a:b——有属性a且值为b的用户集合
a~b——有属性a且值不为b的用户集合
&(a :/~ b)(c :/~ d)——先分别求括号内的用户集合,再求集合交
|(a :/~ b)(c :/~ d)——先分别求括号内的用户集合,再求集合并
3.题解分析
这是一道模拟。数据有原子表达式、简单表达式和嵌套表达式三种。只要求拿70分的话很简单,表达式第一个字符为数字的是原子表达式,第三个字符为数字的是简单表达式。要拿到满分我们需要面对类似“&(&(3:1)(|(1:2)(2:3)))(|(&(2~5)(2~7))(2:5))”这样的字符串。
首先要做的就是解析字符串。因为怕递归可能会超时所以我这里提供一种迭代的方法(菜! 后面知道递归方法也可以解决)。逆向思维从右往左,维护一个集合栈,遇到数字则说明是原子式,立即计算,算完入栈。同一括号内,遇到“&”“|”符号就取栈顶的两个集合进行交并,运算结果再入栈,可以保证我们的运算顺序是对的(因为这两个符号和它的两个表达式相邻)。此时,表达式中的括号成为了无效字符,可以跳过。
处理字符串,我们从len-1往前搜索,每次开始前先跳过括号,如果遇到了数字,则说明接下来要处理一个原子式了,设立一个左标记把它提取出来送到base_expr函数处理,然后更新游标。如果是操作符,则需要进行集合的交并运算。
for(int r=len-1;r>=0;r--)
{
while(str[r]==')'||str[r]=='(')r--;
if(isdigit(str[r]))
{
int l=r-1;
while(l>=0&&(isdigit(str[l])||str[l]==':'||str[l]=='~'))l--;
base_expr(&str[l+1],&str[r+1]);
r=l-1;
}
//集合的交和并
if(r>=0&&str[r]=='&')
its();
else if(r>=0&&str[r]=='|')
uni();
}
因为设计到集合交并,所以使用求集合交并方便且快的bitset。每次从栈中取两个,算完再入栈。
集合的交和并:
inline void its()//交运算
{
bs b1=ss.top();
ss.pop();
b1=b1&ss.top();
ss.pop();
ss.push(b1);
}
inline void uni()//并运算
{
bs b1=ss.top();
ss.pop();
b1=b1|ss.top();
ss.pop();
ss.push(b1);
}
bitset按位表示。第m位为1,则说明集合中有编号m的用户。要使用bitset直接表示max=1e9的DN显然不合理,但是用户数量最多为2500,所以可以使用哈希用数组dnlist下标来映射DN(对应的其他DN编号也换成下标)。
用一个类型为pair二维数组lib表示用户的属性,下标和dnlist一一对应。当求断言时,在lib中找有该属性且为指定值的用户,修改bitset。但是仅仅这样我们无法求反断言式,所以要unordered_map一个属性和用户集合,表示有该属性的用户有哪些,然后我们可以在这些用户里面查找指定pair,断言时查找成功,反断言时查找失败(有该属性但不是指定值),说明满足条件,标记。
void asrt(int aname,int aval,char oper)//断言与反断言
{
bs b;
pit p(aname,aval);
if(oper==':')//断言
{
for(si it=ulib[aname].begin();it!=ulib[aname].end();it++)//获取有该属性的用户
{
if(binary_search(lib[*it].begin(),lib[*it].end(),p))
b.set(*it);
}
}
else//反断言
{
for(si it=ulib[aname].begin();it!=ulib[aname].end();it++)//获取有该属性的用户
{
if(!binary_search(lib[*it].begin(),lib[*it].end(),p))
b.set(*it);
}
}
ss.push(b);
}
最后就是提取bitset,按位映射回dnlist,内容存到ans数组,升序排序再输出。
4.完整代码
#include>
stack<bs>ss;//存每次运算结果
int mystoi(char *s,char *end)
{
int base=1,sum=0;
for(int i=end-s-1;i>=0;i--)
{
sum+=base*(s[i]-'0');
base*=10;
}
return sum;
}
inline void its()//交运算
{
bs b1=ss.top();
ss.pop();
b1=b1&ss.top();
ss.pop();
ss.push(b1);
}
inline void uni()//并运算
{
bs b1=ss.top();
ss.pop();
b1=b1|ss.top();
ss.pop();
ss.push(b1);
}
void asrt(int aname,int aval,char oper)//断言与反断言
{
bs b;
pit p(aname,aval);
if(oper==':')//断言
{
for(si it=ulib[aname].begin();it!=ulib[aname].end();it++)//获取有该属性的用户
{
if(binary_search(lib[*it].begin(),lib[*it].end(),p))
b.set(*it);
}
}
else//反断言
{
for(si it=ulib[aname].begin();it!=ulib[aname].end();it++)//获取有该属性的用户
{
if(!binary_search(lib[*it].begin(),lib[*it].end(),p))
b.set(*it);
}
}
ss.push(b);
}
void base_expr(char *expr,char *end)//解析原子表达式
{
int op=0;
while(expr[op]!=':'&&expr[op]!='~')op++;
int num1,num2;
num1=mystoi(expr,&expr[op]);
num2=mystoi(&expr[op+1],end);
asrt(num1,num2,expr[op]);
}
int main()
{
scanf("%d",&n);
lib.resize(n+1);
for(int i=1;i<=n;i++)//建表
{
int DN,attnum,attname,attv;
scanf("%d%d",&DN,&attnum);
dnlist[i]=DN;
lib[i].resize(attnum);
for(int j=0;j<attnum;j++)
{
scanf("%d%d",&attname,&attv);
lib[i][j]=pit(attname,attv);
ulib[attname].insert(i);
}
sort(lib[i].begin(),lib[i].end());
}
scanf("%d",&m);
for(int i=0;i<m;i++)
{
scanf("%s",str);
int len=strlen(str);
for(int r=len-1;r>=0;r--)
{
while(str[r]==')'||str[r]=='(')r--;
if(isdigit(str[r]))
{
int l=r-1;
while(l>=0&&(isdigit(str[l])||str[l]==':'||str[l]=='~'))l--;
base_expr(&str[l+1],&str[r+1]);
r=l-1;
}
//集合的交和并
if(r>=0&&str[r]=='&')
its();
else if(r>=0&&str[r]=='|')
uni();
}
if(!ss.empty())
{
int index=0;
bs ansbs=ss.top();
for(int i=1;i<=n;i++)
if(ansbs[i]==1)
ans[index++]=dnlist[i];
sort(ans,ans+index);
for(int i=0;i<index;i++)
printf("%d ",ans[i]);
}
printf("\n");
while(!ss.empty())ss.pop();
}
return 0;
}
后面可能还会分析历年的csp题目。实力实在有限,但在分析的过程中也学到了很多。
另外就是,都看到这里了,能不能给个小小的赞鼓励一下——