【数据结构与算法】并查集

一、并查集的概念

并查集是一个树形结构，所谓的并查，就是当我们有了一个节点，我们就能知道这个节点属于哪个集合。

举个例子理解以下：战国时期有很多国家，它们会互相打仗，那么现在有两个互相不认识的人，如何知道对方是敌是友呢？

现在有一种方法：每个国家都有一个大王，我们只要知道自己的上级，上级在知道他的上级，一层层往上，就能找到他的大王是谁，这样就能知道两个人是否是一个国家的了。

二、并查集的实现

首先我们需要一个整型数组p[]它记录的是每个节点的前驱节点。
然后需要find(x)函数，作用是用于查找指定节点x于哪个集合.
函数join(x1,x2) 用于合并两个节点 x1 和 x2

2.1 find()的实现

上面说了我们要确定自己的大王是谁，就可以一层一层的向上询问。
所以我们可以用find来找到节点的根。

int find(int x)					
{
	while(p[x] != x)// 一层层的向上找
		x = p[x];				
	return x;					
}

2.2 路径压缩算法

我们发现如果我们每次都一层一层的向上查找太消耗时间了，所以我们可以在查找的过程把路径压缩。

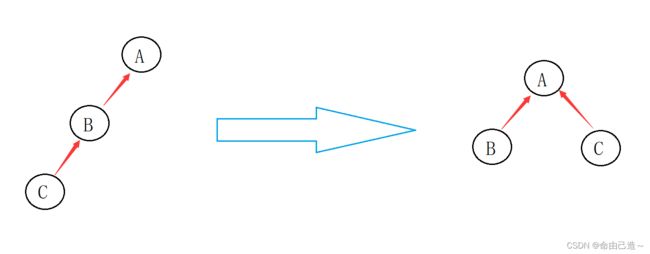
int find(int x)
{
    // 路径压缩
    if(p[x] != x) p[x] = find(p[x]);//递归出口：x的上级为 x本身，即 x为根结点  
    return p[x];
}

注意这里第一次查找的时候是没有压缩效果的，第二次及以后才会有效果。

2.3 join()的实现

join就是把两个本来不相关的节点放到一个集合里面，具体实现我们可以借用find函数，对于join(x1,x2)，我们只需要让x1的上级变成x2的上级即可。

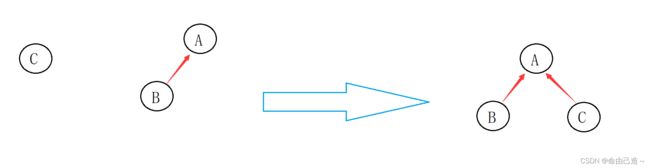
void join(int x1, int x2)
{
    p[find(x1)] = find(x2);
}

三、并查集的应用

3.1 例题：合并集合

题目链接

题目描述：

一共有 n个数，编号是 1∼n，最开始每个数各自在一个集合中。
现在要进行 m个操作，操作共有两种：
M a b，将编号为 a 和 b
的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 a 和 b的两个数是否在同一个集合中；

输入格式

第一行输入整数 n 和 m。
接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。
每个结果占一行。

数据范围

1≤n,m≤1e5

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

#include 

using namespace std;

const int N = 1e5 + 10;
int p[N];

int find(int x)
{
    // 路径压缩
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void join(int x1, int x2)
{
    p[find(x1)] = find(x2);
}

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        p[i] = i;
    }
    while(m--)
    {
        char op;
        int x1, x2;
        cin >> op >> x1 >> x2;
        if(op == 'M')
        {
            join(x1, x2);
        }
        else
        {
            if(find(x1) == find(x2))
            {
                cout << "Yes" << endl;
            }
            else
            {
                cout << "No" << endl;
            }
        }
    }
    return 0;
}

3.2 例题：连通块中点的数量

题目描述：

给定一个包含 n 个点（编号为 1∼n）的无向图，初始时图中没有边。
现在要进行 m 个操作，操作共有三种：
C a b，在点 a 和点 b 之间连一条边，a 和 b 可能相等；
Q1 a b，询问点 a 和点 b 是否在同一个连通块中，a 和 b 可能相等；
Q2 a，询问点 a 所在连通块中点的数量；

输入格式

第一行输入整数 n 和 m。
接下来 m 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式

对于每个询问指令 Q1 a b，如果 a 和 b 在同一个连通块中，则输出 Yes，否则输出 No。
对于每个询问指令 Q2 a，输出一个整数表示点 a 所在连通块中点的数量，每个结果占一行。

数据范围

1≤n,m≤1e5

输入样例：

5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5

输出样例：

Yes
2
3

思路分析：
这道题跟上面一道题的不同是这里需要求一个集合有多少个元素，我们的方法是添加一个cnt数组，让每个集合的根节点来记录这个集合里有多少个元素。
具体的做法是在join中处理cnt数组，因为查找find并不会改变该集合的元素个数。

void join(int x1, int x2)
{
    cnt[find(x2)] += cnt[find(x1)];
    p[find(x1)] = find(x2);
}

这里要注意顺序不能改变，如果把p[find(x1)] = find(x2);放在前面，find(x1)的根就会发生了变化。所以要先处理cnt数组。

#include 
#include 

using namespace std;

const int N = 1e5 + 10;
int p[N], cnt[N];

int find(int x)
{
    if(p[x] != x)
    {
        p[x] = find(p[x]);
    }
    return p[x];
}

void join(int x1, int x2)
{
    cnt[find(x2)] += cnt[find(x1)];
    p[find(x1)] = find(x2);
}

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        p[i] = i;
        cnt[i] = 1;
    }
    while(m--)
    {
        string op;
        int a, b;
        cin >> op;
        if(op == "C")
        {
            cin >> a >> b;
            if(find(a) != find(b))
            {
                join(a, b);
            }
        }
        else if(op == "Q1")
        {
            cin >> a >> b;
            if(find(a) == find(b))
            {
                cout << "Yes" << endl;
            }
            else
            {
                cout << "No" << endl;
            }
        }
        else
        {
            cin >> a;
            cout << cnt[find(a)] << endl;
        }
    }
    return 0;
}

四、总结

1️⃣ 我们一般用集合中的某个元素来代表这个集合，则该元素称为此集合的代表元。
2️⃣ 对于每一个元素 x，pre[x] 存放 x 在树形结构中的父亲节点（如果 x 是根节点，则令pre[x] = x）

一般来说，一个并查集对应两个操作：

1. 查找函数（ Find()函数 ）
2. 合并集合函数（ Join()函数 ）

---

---