剑指offer 81题-Python版本(前37DP之前)-Java版本(后43DP开始)
文章目录
- 目录
- 1、数据结构
-
- 1.1 链表
-
- JZ18 删除链表的节点
- 1.2 树
-
- JZ55 二叉树的深度
- JZ77 按之字形顺序打印二叉树
- JZ54 二叉搜索树的第k个节点
- JZ7 重建二叉树
- JZ27 二叉树的镜像
- JZ26 树的子结构
- JZ32 从上往下打印二叉树
- JZ33 二叉搜索树的后序遍历序列
- JZ82 二叉树中和为某一值的路径(一)
- JZ34 二叉树中和为某一值的路径(二)
- JZ36 二叉搜索树与双向链表
- JZ79 判断是不是平衡二叉树
- JZ8 二叉树的下一个结点
- JZ28 对称的二叉树
- JZ78 把二叉树打印成多行
- JZ37 序列化二叉树 ▲▲
- JZ84 二叉树中和为某一值的路径(三) ▲
- JZ86 在二叉树中找到两个节点的最近公共祖先 (TODO 递归解法还不懂)
- 1.3 队列 & 栈
-
- JZ9 用两个栈实现队列
- JZ30 包含min函数的栈
- JZ31 栈的压入、弹出序列
- JZ73 翻转单词序列
- JZ59 滑动窗口的最大值 (# 双队列法:TODO)
- 2、算法
-
- 2.1 搜索算法
-
- JZ53 数字在升序数组中出现的次数
- JZ4 二维数组中的查找
- JZ11 旋转数组的最小数字
- JZ38 字符串的排列 (TODO)
- JZ44 数字序列中某一位的数字
- 2.2 动态规划
-
- JZ42 连续子数组的最大和
- JZ85 连续子数组的最大和(二)
- JZ69 跳台阶
- JZ10 斐波那契数列
- JZ71 跳台阶扩展问题
- JZ19 正则表达式匹配 (HARD)
- JZ63 买卖股票的最好时机(一)
- JZ70 矩形覆盖
- JZ47 礼物的最大价值
- JZ48 最长不含重复字符的子字符串
- JZ46 把数字翻译成字符串
- JZ12 矩阵中的路径
- JZ13 机器人的运动范围
- JZ3 数组中重复的数字
- JZ51 数组中的逆序对
- JZ40 最小的K个数
- JZ41 数据流中的中位数
- JZ65 不用加减乘除做加法
- JZ15 二进制中1的个数
- JZ16 数值的整数次方
- JZ56 数组中只出现一次的两个数字
- JZ64 求1+2+3+...+n
- JZ29 顺时针打印矩阵
- JZ61 扑克牌顺子
- JZ67 把字符串转换成整数(atoi)
- JZ20 表示数值的字符串
- JZ66 构建乘积数组
- JZ50 第一个只出现一次的字符
- JZ5 替换空格
- JZ21 调整数组顺序使奇数位于偶数前面(一)
- JZ39 数组中出现次数超过一半的数字
- JZ43 整数中1出现的次数(从1到n整数中1出现的次数)
- JZ45 把数组排成最小的数
- JZ49 丑数
- JZ74 和为S的连续正数序列
- JZ57 和为S的两个数字
- JZ58 左旋转字符串
- JZ62 孩子们的游戏(圆圈中最后剩下的数)
- JZ75 字符流中第一个不重复的字符
- JZ14 剪绳子
- JZ81 调整数组顺序使奇数位于偶数前面(二)
- JZ83 剪绳子(进阶版)
- JZ17 打印从1到最大的n位数
目录
1、数据结构
1.1 链表
MyList.py
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def show(self):
p = self
while p is not None:
print(p.val, end=' ')
p = p.next
print()
# 只返回头节点
def Create(data):
# print('data',data)
if len(data) < 1:
return None
head = ListNode(data[0])
tail = head
for i in range(1, len(data)):
tail.next = ListNode(data[i])
tail = tail.next
return head
# 返回头节点和尾节点
def Create2(data):
# print('data',data)
if len(data) < 1:
return None, None
head = ListNode(data[0])
tail = head
for i in range(1, len(data)):
tail.next = ListNode(data[i])
tail = tail.next
return head, tail
def CreateJZ52(list1, list2, list3):
p1, t1 = Create2(list1)
p2, t2 = Create2(list2)
tail = Create(list3)
if p1:
t1.next = tail
else:
p1 = tail
if p2:
t2.next = tail
else:
p2 = tail
return p1, p2
# list1 = Create([1, 2, 3])
# list1.show()
# p1, p2 = CreateJZ52([1, 2, 3], [4, 5], [6, 7])
# p1.show()
# p2.show()
MyList2.py
class RandomListNode:
def __init__(self, x):
self.label = x
self.next = None
self.random = None
def findByVale(self, x):
if x == '#':
return None
p = self
while p:
if p.label == x:
return p
p = p.next
return None
def __str__(self):
h = self
while h:
print(h.label, end=' ')
h = h.next
h = self
while h:
if h.random == None:
print('#', end=' ')
else:
print(h.random.label, end=' ')
h = h.next
return '\n'
def Create(data, rp):
if len(data) < 1:
return None
# 建立主链表
head = RandomListNode(data[0])
tail = head
for i in data[1:]:
tail.next = RandomListNode(i)
tail = tail.next
# 建立随机指针
p = head
for i in rp:
p.random = head.findByVale(i)
p = p.next
return head
if __name__ == '__main__':
data = [1, 2, 3, 4, 5]
rp = [3, 5, '#', 2, '#']
root = Create(data, rp)
print(root)
JZ18 删除链表的节点
JZ18 删除链表的节点
from myutils.MyList import *
class Solution:
def deleteNode(self, head: ListNode, val: int) -> ListNode:
phead = ListNode(-1) # 新链表上慢慢插入
tail = phead
while head:
if head.val != val:
tail.next = head
tail = tail.next
head = head.next
tail.next = None
return phead.next
if __name__ == '__main__':
head = Create([2, 5, 1, 9])
delVal = 5
Solution().deleteNode(head, delVal).show()
1.2 树
MyTree.py
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def levelOrder(self):
q = [self]
while q:
top = q.pop(0)
print(top.val, end=' ')
if top.left:
q.append(top.left)
if top.right:
q.append(top.right)
def preOrder(self):
if self is None: return
print(self.val, end=' ')
if self.left: self.left.preOrder() # 参数self以调用者形式传入
if self.right: self.right.preOrder()
def midOrder(self):
if self is None: return
if self.left: self.left.midOrder()
print(self.val, end=' ')
if self.right: self.right.midOrder()
def afterOrder(self):
if self is None: return
if self.left: self.left.afterOrder()
if self.right: self.right.afterOrder()
print(self.val, end=' ')
def newNode(x):
if x == '#':
return None
return TreeNode(x)
def levelCreate(data): # 根据数组data层序创建二叉树
if len(data) < 1: return None
i = 0
root = TreeNode(data[i]) # 当作引用传入 必须事前开辟内存,绝对不能是None
i += 1
q = [root]
while i < len(data):
top = q.pop(0)
if i < len(data):
top.left = newNode(data[i])
if top.left: q.append(top.left) # 非空入队 子树上接着插
i += 1
if i < len(data):
top.right = newNode(data[i])
if top.right: q.append(top.right)
i += 1
return root
if __name__ == '__main__':
data = [1, 2, 3, 4, 5, '#', 6, '#', '#', 7]
root = levelCreate(data)
root.levelOrder()
print('层序')
root.preOrder()
print('先序')
root.midOrder()
print('中序')
root.afterOrder()
print('后序')
JZ55 二叉树的深度
JZ55 二叉树的深度
from myutils.MyTree import *
class Solution:
def TreeDepth(self, pRoot: TreeNode) -> int:
if pRoot is None: return 0
return max(self.TreeDepth(pRoot.left), self.TreeDepth(pRoot.right)) + 1
if __name__ == '__main__':
data = [1, 2, 3, 4, 5, '#', 6, '#', '#', 7]
root = levelCreate(data)
root.levelOrder()
print('层序')
ans = Solution().TreeDepth(root)
print(ans)
JZ77 按之字形顺序打印二叉树
JZ77 按之字形顺序打印二叉树
from myutils.MyTree import *
from typing import List
class Solution:
def Print(self, pRoot: TreeNode) -> List[List[int]]:
if pRoot is None: return None
q = [pRoot]
left = True # True:left->right False:right->left
ans = []
while q:
l = len(q)
t = []
for i in range(l):
top = q.pop(0)
t.append(top.val)
if top.left:
q.append(top.left)
if top.right:
q.append(top.right)
if left:
ans.append(t)
else:
ans.append(t[::-1])
left =not left
return ans
if __name__ == '__main__':
pRoot = levelCreate([1, 2, 3, '#', '#', 4, 5])
pRoot = levelCreate([])
# pRoot.levelOrder()
print('层序')
ans = Solution().Print(pRoot)
print(ans)
JZ54 二叉搜索树的第k个节点
JZ54 二叉搜索树的第k个节点
from myutils.MyTree import *
class Solution:
ans = -1 # 类属性(静态属性)
count = 0 # 类属性(静态属性)
# 中序遍历第k个结点
def KthNode(self, proot: TreeNode, k: int) -> int:
if proot is None: return -1
if Solution.count > k: return
if proot.left: self.KthNode(proot.left, k)
# print(proot.val)
Solution.count += 1
if Solution.count == k:
Solution.ans = proot.val
return Solution.ans
if proot.right: self.KthNode(proot.right, k)
return Solution.ans
if __name__ == '__main__':
data = [5, 3, 7, 2, 4, 6, 8]
k = 3
# data = []
proot = levelCreate(data)
# proot.levelOrder()
# print('层序')
ans = Solution().KthNode(proot, k)
print(ans)
JZ7 重建二叉树
JZ7 重建二叉树
from myutils.MyTree import *
from typing import List
class Solution:
def reConstructBinaryTree(self, pre: List[int], vin: List[int]) -> TreeNode:
if len(pre) < 1: return None
# k = 0
# while vin[k] != pre[0]: k += 1
k = vin.index(pre[0]) # python不需要循环 直接找
root = TreeNode(pre[0])
root.left = self.reConstructBinaryTree(pre[1:k + 1], vin[:k])
root.right = self.reConstructBinaryTree(pre[k+1:], vin[k+1:])
return root
if __name__ == '__main__':
pre = [1, 2, 4, 7, 3, 5, 6, 8]
vin = [4, 7, 2, 1, 5, 3, 8, 6]
ans = Solution().reConstructBinaryTree(pre,vin)
ans.levelOrder()
JZ27 二叉树的镜像
JZ27 二叉树的镜像
from myutils.MyTree import *
class Solution:
def Mirror(self, pRoot: TreeNode) -> TreeNode:
if pRoot is None: return None
pRoot.left, pRoot.right = pRoot.right, pRoot.left # 交换左右节点
self.Mirror(pRoot.left) # 递归执行
self.Mirror(pRoot.right)
return pRoot
if __name__ == '__main__':
data = [8, 6, 10, 5, 7, 9, 11]
# data = []
pRoot = levelCreate(data)
pRoot.levelOrder()
print('层序')
ans = Solution().Mirror(pRoot)
pRoot.levelOrder()
JZ26 树的子结构
JZ26 树的子结构
参考之前1刷时的java解法
难点: 两个子树的判断(是否有子关系),需要单独拎出来
同步遍历:
树1跟着树2遍历 树2有的树1都有 直到树2遍历完 返回True 【可以树1有,树2没有,仍返回True,也就是树1跟着树2遍历即可 例如层序跟着树2,可以少入队一些结点】
否则: 树1没有(树2有)或者值不同 都返回False
- 解法一:递归解法,两次递归,实难原创,真不好理解
from myutils.MyTree import *
class Solution:
def HasSubtree(self, pRoot1: TreeNode, pRoot2: TreeNode) -> bool:
# 找到val相同的根 开始同步遍历 (难点在于,这里也需要递归)
if not pRoot1 or not pRoot2: return False # 1或者2有一个为空 就没办法比较了 此分支绝对为False
if pRoot1.val == pRoot2.val: # 先序遍历找相同根
if self.judge(pRoot1, pRoot2): # 一旦是子结构,立刻就可以终止
return True
return self.HasSubtree(pRoot1.left, pRoot2) or self.HasSubtree(pRoot1.right, pRoot2)
# 只判断两颗子树是否是相同结构 逻辑有点复杂得慢慢理
# [核心同步遍历]拆分出来
def judge(self, pRoot1: TreeNode, pRoot2: TreeNode) -> bool:
if not pRoot2: return True # 树2先没了(树1多点没关系!!)(或者一起没 正好完全一样) 都可以正常结束了 其实就是树2正常遍历结束就OK
# (树1多点没关系!!好好理解 树1多了可以忽略,因为此处(此次递归)返回True 直到树2遍历完)
if not pRoot1 or pRoot1.val != pRoot2.val: return False # 此处保证树2还有 但是:树1没有或者二者不等 就也不行了
# 下面 pRoot1和pRoot2都不为空了
return self.judge(pRoot1.left, pRoot2.left) and self.judge(pRoot1.right, pRoot2.right)
if __name__ == '__main__':
t1 = [8, 8, 7, 9, 2, '#', '#', '#', '#', 4, 7]
t2 = [8, 9, 2]
pRoot1 = levelCreate(t1)
pRoot2 = levelCreate(t2)
pRoot1.levelOrder()
print('树A层序')
pRoot2.levelOrder()
print('树B层序')
ans = Solution().HasSubtree(pRoot1, pRoot2)
print(ans)
- 解法二:judge部分不用递归,层序遍历,这样就只有一个递归了(好理解一点 但还是难,还是要把同步遍历单独拆出来)
from myutils.MyTree import *
class Solution:
def HasSubtree(self, pRoot1: TreeNode, pRoot2: TreeNode) -> bool:
# 此处仍然可以递归
if not pRoot1 or not pRoot2: return False # 此分支肯定不行 pRoot2一直是同一个值
if pRoot1.val == pRoot2.val: # 有了上面的判断 一定都不为None了
if self.judge(pRoot1, pRoot2):
return True
return self.HasSubtree(pRoot1.left, pRoot2) or self.HasSubtree(pRoot1.right, pRoot2)
# 同步遍历(层序)
# 树1跟着树2遍历 树2有的树1都有 直到树2遍历完 返回True
# 否则: 树1没有或者值不同 都返回False
def judge(self, pRoot1: TreeNode, pRoot2: TreeNode) -> bool:
q1 = [pRoot1]
q2 = [pRoot2]
while len(q2) > 0:# 注意是大于0
top1 = q1.pop(0)
top2 = q2.pop(0)
if not top1 and top2: return False # 跟着树2入队 树2层序正常 树1没有了 肯定不是 【其实top2一定不为None】
if top1.val != top2.val: return False # 值不相等 也没办法了
if top2.left: # 跟着树2遍历
q1.append(top1.left)
q2.append(top2.left)
if top2.right:
q1.append(top1.right)
q2.append(top2.right)
return True # 跟着树2正常遍历完
if __name__ == '__main__':
t1 = [8, 8, 7, 9, 2, '#', '#', '#', '#', 4, 7]
t2 = [8, 9, 2]
t1 = [1, 2, 3]
t2 = [2, 3, '#']
pRoot1 = levelCreate(t1)
pRoot2 = levelCreate(t2)
pRoot1.levelOrder()
print('树A层序')
pRoot2.levelOrder()
print('树B层序')
ans = Solution().HasSubtree(pRoot1, pRoot2)
print(ans)
前面2种方式都过于依赖先序遍历 (导致有了递归,看起来好难 其实简单理解为先序遍历,也还好)
下面这种方式完全用层序遍历 理解起来就简单多了
- 解法三:完全没有递归,全部改成层序遍历(好理解一点 但还是难,还是要把同步遍历单独拆出来)
from myutils.MyTree import *
class Solution:
def HasSubtree(self, pRoot1: TreeNode, pRoot2: TreeNode) -> bool:
# 此处也不要递归
if not pRoot1 or not pRoot2: return False # 开始执行一次 有一个为空都不行
q = [pRoot1]
while len(q) > 0: # 注意是大于0
top = q.pop(0)
if top.val == pRoot2.val: # 正常层序遍历找pRoot2根相同的结点
if self.judge(top, pRoot2): # 层序遍历该做的事儿
return True
if top.left:
q.append(top.left)
if top.right:
q.append(top.right)
return False # 遍历结束都没找到 不行啦
# 同步遍历(层序)
# 树1跟着树2遍历 树2有的树1都有 直到树2遍历完 返回True
# 否则: 树1没有或者值不同 都返回False
def judge(self, pRoot1: TreeNode, pRoot2: TreeNode) -> bool:
q1 = [pRoot1]
q2 = [pRoot2]
while len(q2) > 0: # 注意是大于0
top1 = q1.pop(0)
top2 = q2.pop(0)
if not top1 and top2: return False # 跟着树2入队 树2层序正常 树1没有了 肯定不是 【其实top2一定不为None】
if top1.val != top2.val: return False # 值不相等 也没办法了
if top2.left: # 跟着树2遍历
q1.append(top1.left)
q2.append(top2.left)
if top2.right:
q1.append(top1.right)
q2.append(top2.right)
return True # 跟着树2正常遍历完
if __name__ == '__main__':
t1 = [8, 8, 7, 9, 2, '#', '#', '#', '#', 4, 7]
t2 = [8, 9, 2]
t1 = [1, 2, 3]
t2 = [2, 3, '#']
t1 = [1, 2, 3, 4]
t2 = [3]
pRoot1 = levelCreate(t1)
pRoot2 = levelCreate(t2)
pRoot1.levelOrder()
print('树A层序')
pRoot2.levelOrder()
print('树B层序')
ans = Solution().HasSubtree(pRoot1, pRoot2)
print(ans)
JZ32 从上往下打印二叉树
JZ32 从上往下打印二叉树
纯水题 就是一个层序遍历
from myutils.MyTree import *
from typing import *
class Solution:
def PrintFromTopToBottom(self, root: TreeNode) -> List[int]:
if not root: return None
ans = []
q = [root]
while len(q)>0:
top = q.pop(0)
ans.append(top.val)
if top.left: q.append(top.left)
if top.right: q.append(top.right)
return ans
if __name__ == '__main__':
data = [8, 6, 10, '#', '#', 2, 1]
root = levelCreate(data)
ans = Solution().PrintFromTopToBottom(root)
print(ans)
JZ33 二叉搜索树的后序遍历序列
JZ33 二叉搜索树的后序遍历序列
之前一刷的java版本
from myutils.MyTree import *
from typing import *
class Solution:
def VerifySquenceOfBST(self, sequence: List[int]) -> bool:
if len(sequence) < 1: return False
vim = sorted(sequence)
return self.CreateBST(vim, sequence)
# 还原二叉树 能还原返回True 否则返回False
def CreateBST(self, vin: List[int], after: List[int]) -> bool:
# if len(after) != len(vin): return False # 左右不等 False # 注释了也能过
if len(after) < 1: return True # 空是正常的 (此处二者长度一定相等了)
if not after[-1] in vin: return False
k = vin.index(after[-1])
return self.CreateBST(vin[:k], after[:k]) and self.CreateBST(vin[k + 1:], after[k:-1]) #不需要真的创建,调用过程即可
if __name__ == '__main__':
data = [5, 7, 6, 9, 11, 10, 8]
# data = [1, 3, 2]
# data = [3, 1, 2]
# data = []
ans = Solution().VerifySquenceOfBST(data)
print(ans)
JZ82 二叉树中和为某一值的路径(一)
JZ82 二叉树中和为某一值的路径(一)
from myutils.MyTree import *
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root: return False # [] 0 特殊数据集导致的 必须这么写
if not root.left and not root.right: return sum-root.val == 0 # 必须提前判断 (这里唯一True) # 真是叶子结点就不会再往下了
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
if __name__ == '__main__':
data = [5, 4, 8, 1, 11, '#', 9, '#', '#', 2, 7]
sum = 22
# data = [1, 2]
# sum = 3
# data = []
# sum = 0
# data = [1, 2]
# sum = 0
root = levelCreate(data)
ans = Solution().hasPathSum(root, sum)
print(ans)
JZ34 二叉树中和为某一值的路径(二)
JZ34 二叉树中和为某一值的路径(二)
from myutils.MyTree import *
from typing import *
import queue
class Solution:
# 要记录所有的路径 层序遍历吧
def FindPath(self, root: TreeNode, target: int) -> List[List[int]]:
self.DFSPath(root, [], target)
return self.ans
ans = []
def DFSPath(self, root: TreeNode, path, target: int):
if not root: return
path.append(root.val)
if not root.left and not root.right and target - root.val == 0: self.ans.append(path)
if root.left: self.DFSPath(root.left, path.copy(), target - root.val) # 注意copy一份 不要直接传递引用
if root.right: self.DFSPath(root.right, path.copy(), target - root.val)
if __name__ == '__main__':
data = [10, 5, 12, 4, 7]
target = 22
root = levelCreate(data)
ans = Solution().FindPath(root,target)
print(ans)
其实Python类方法中可以直接定义方法来用的
from myutils.MyTree import *
from typing import *
import queue
class Solution:
# 要记录所有的路径 层序遍历吧
def FindPath(self, root: TreeNode, target: int) -> List[List[int]]:
ans = []
def DFSPath(root: TreeNode, path, target: int):
if not root: return
path.append(root.val)
if not root.left and not root.right and target - root.val == 0: ans.append(path)
if root.left: DFSPath(root.left, path.copy(), target - root.val) # 注意copy一份 不要直接传递引用
if root.right: DFSPath(root.right, path.copy(), target - root.val)
DFSPath(root, [], target)
return ans
if __name__ == '__main__':
data = [10, 5, 12, 4, 7]
target = 22
root = levelCreate(data)
ans = Solution().FindPath(root,target)
print(ans)
再次改进,简化参数,全用‘全局变量’
from myutils.MyTree import *
from typing import *
import queue
class Solution:
# 要记录所有的路径 层序遍历吧
def FindPath(self, root: TreeNode, target: int) -> List[List[int]]:
ans, path = [], []
def DFSPath(root: TreeNode, target: int):
if not root: return
path.append(root.val)
if not root.left and not root.right and target - root.val == 0: ans.append(path[:]) # 必须写path[:]测才行
if root.left: DFSPath(root.left, target - root.val)
if root.right: DFSPath(root.right, target - root.val)
path.pop() # 每次退栈时弹出
DFSPath(root, target)
return ans
if __name__ == '__main__':
data = [10, 5, 12, 4, 7]
target = 22
root = levelCreate(data)
ans = Solution().FindPath(root, target)
print(ans)
JZ36 二叉搜索树与双向链表
JZ36 二叉搜索树与双向链表
from myutils.MyTree import *
class Solution:
pre, root = None, None
# 简单中序遍历+维护一个pre
def Convert(self, pRootOfTree):
if not pRootOfTree: return
self.Convert(pRootOfTree.left)
if self.pre: self.pre.right = pRootOfTree
pRootOfTree.left = self.pre
Solution.pre = pRootOfTree
if not self.root: Solution.root = pRootOfTree # 第一个遍历的结点是首结点
self.Convert(pRootOfTree.right)
return Solution.root
if __name__ == '__main__':
data = [10, 6, 14, 4, 8, 12, 16]
data = [5, 4, '#', 3, '#', 2, '#', 1]
root = levelCreate(data)
root.levelOrder()
print('层序')
root.midOrder()
print('中序')
ans = Solution().Convert(root)
while ans:
print(ans.val, end=' ')
ans = ans.right
JZ79 判断是不是平衡二叉树
JZ79 判断是不是平衡二叉树
from myutils.MyTree import *
class Solution:
def IsBalanced_Solution(self, pRoot: TreeNode) -> bool:
def getHight(root):
if not root: return 0
return max(getHight(root.left), getHight(root.right)) + 1
self.flag = True
def judgeBalance(pRoot: TreeNode):
if not pRoot: return
if not self.flag: return
if abs(getHight(pRoot.left) - getHight(pRoot.right)) > 1:
self.flag = False
return
judgeBalance(pRoot.left)
judgeBalance(pRoot.right)
judgeBalance(pRoot)#可别忘记调用了啊
return self.flag
if __name__ == '__main__':
data = [1, 2, 3, 4, 5, 6, 7]
data = []
data = [1, 2, '#', 3, '#', 4, '#', 5]
root = levelCreate(data)
ans = Solution().IsBalanced_Solution(root)
print(ans)
JZ8 二叉树的下一个结点
JZ8 二叉树的下一个结点
from myutils.MyTree2 import *
class Solution:
ans, pre = None, None
def GetNext(self, pNode):
root = pNode
while root.next: root = root.next # 先找到根
def MidNext(root):
if not root: return
if self.ans: return
MidNext(root.left)
if self.pre == pNode:
self.ans = root
self.pre = root # 不写回退时会出错 全局变量的弊端
return
self.pre = root # 维护中序前驱
MidNext(root.right)
MidNext(root)
return self.ans
if __name__ == '__main__':
data = [8, 6, 10, 5, 7, 9, 11]
val = 8
# data = [5]
# val = 5
root = levelCreate(data) # 有父亲指针
pNode = GetNodeByVal(root,val)
ans = Solution().GetNext(pNode)
if ans:
print(ans.val)
else:
print(ans)
- MyTree2.py
from typing import *
'''
MyTree.py基础上加了父亲指针
'''
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
self.next = None # 指向父亲节点
def levelOrder(self):
q = [self]
while q:
top = q.pop(0)
print(top.val, end=' ')
if top.left:
q.append(top.left)
if top.right:
q.append(top.right)
def preOrder(self):
if self is None: return
print(self.val, end=' ')
if self.left: self.left.preOrder() # 参数self以调用者形式传入
if self.right: self.right.preOrder()
def midOrder(self):
if self is None: return
if self.left: self.left.midOrder()
print(self.val, end=' ')
if self.right: self.right.midOrder()
def afterOrder(self):
if self is None: return
if self.left: self.left.afterOrder()
if self.right: self.right.afterOrder()
print(self.val, end=' ')
def newNode(x):
if x == '#':
return None
return TreeNode(x)
def levelCreate(data): # 根据数组data层序创建二叉树
if len(data) < 1: return None
i = 0
root = TreeNode(data[i]) # 当作引用传入 必须事前开辟内存,绝对不能是None
i += 1
q = [root]
while i < len(data):
top = q.pop(0)
if i < len(data):
top.left = newNode(data[i])
if top.left:
q.append(top.left) # 非空入队 子树上接着插
top.left.next = top # 父亲指针
i += 1
if i < len(data):
top.right = newNode(data[i])
if top.right:
q.append(top.right)
top.right.next = top # 父亲指针
i += 1
# addNext(root)
return root
def midParent(root):
if not root: return
midParent(root.left)
print(root.val, end=' ')
if root.next:
print(root.next.val)
else:
print()
midParent(root.right)
def GetNodeByVal(root, val):
if not root: return None
if root.val == val: return root
findL = GetNodeByVal(root.left, val)
if findL: return findL
findR = GetNodeByVal(root.right, val)
if findR: return findR
if __name__ == '__main__':
data = [8, 6, 10, 5, 7, 9, 11]
root = levelCreate(data)
midParent(root)
print('find',9)
print(GetNodeByVal(root,9).val)
'''层序一个个查找到None再插入不行
# 层序创建: 层序遍历(查找)遇到空就插入
def leveladd(root, node): # 往树root里插入结点node python默认就是传递引用root
if root is None:
root = node
return
q = [root]
while q: # 层序遍历 遇到None就是插入位置
top = q.pop(0) # 出队
if top.left is None: # 遍历左孩子(左孩子为空 直接找到了 插入呀)
top.left = node
return
else: # 可能要接着往下层找 入队 以进行层序遍历
q.append(top.left) # 左入队 (正常层序遍历操作)
if top.right is None: # 左孩子不空 右孩子空 插入右孩子
top.right = node
return
else: # 可能要接着往下层找 入队 以进行层序遍历
q.append(top.right)
# 插入借点写好了 创建就简单了(BST思想)
def levelCreate(data): # 根据数组data层序创建二叉树
if len(data) < 1: return None
root = TreeNode(data[0]) # 当作引用传入 必须事前开辟内存,绝对不能是None
for i in data[1:]:
leveladd(root, TreeNode(i))
return root
'''
JZ28 对称的二叉树
JZ28 对称的二叉树
from myutils.MyTree import *
class Solution:
def isSymmetrical(self, pRoot: TreeNode) -> bool:
return self.symmetry(pRoot, pRoot)
def symmetry(self, r1, r2):
if not r1 and not r2: return True
# print(r1.val, r2.val)
if (not r1 and r2) or (not r2 and r1): return False # 一个为空 一个不空 肯定不行
if r1.val != r2.val: return False # 注意是值不等
return self.symmetry(r1.left, r2.right) and self.symmetry(r1.right, r2.left)
if __name__ == '__main__':
data = [1, 2, 2, 3, 4, 4, 3]
data = [8, 6, 9, 5, 7, 7, 5]
data = [1, 2]
root = levelCreate(data)
ans = Solution().isSymmetrical(root)
print(ans)
JZ78 把二叉树打印成多行
JZ78 把二叉树打印成多行
from myutils.MyTree import *
import queue
class Solution:
def Print(self, pRoot: TreeNode) -> List[List[int]]:
ans = []
q = queue.Queue()
if pRoot: q.put(pRoot)
while not q.empty():
N = q.qsize()
t = []
for i in range(N):
top = q.get()
t.append(top.val)
if top.left: q.put(top.left)
if top.right: q.put(top.right)
ans.append(t)
return ans
if __name__ == '__main__':
data = [1, 2, 3, '#', '#', 4, 5]
root = levelCreate(data)
ans = Solution().Print(root)
print(ans)
JZ37 序列化二叉树 ▲▲
JZ37 序列化二叉树
from myutils.MyTree import *
import queue
class Solution:
def Serialize(self, root):
ans = '{'
q = queue.Queue()
if root:
q.put(root)
ans += f'{root.val}'
while not q.empty():
top = q.get()
if top.left:
q.put(top.left)
ans += f',{top.left.val}'
else: ans += ',#'
if top.right:
q.put(top.right)
ans += f',{top.right.val}'
else: ans += ',#'
return ans.rstrip('#,') + '}'
def Deserialize(self, s):
data = s.strip('{}').split(',')
if len(data) < 1 or data[0]=='': return None
q = queue.Queue()
root = self.NewNode(data[0])
q.put(root)
i = 1
while i < len(data):
top = q.get()
if i < len(data):
top.left = self.NewNode(data[i])
if top.left: q.put(top.left)
i += 1
if i < len(data):
top.right = self.NewNode(data[i])
if top.right: q.put(top.right)
i += 1
return root
def NewNode(self, val):
if val == '#': return None
return TreeNode(int(val)) # 注意val是int类型 不能是string
if __name__ == '__main__':
s = '{1,2,3,#,#,6,7}'
s = '{}'
root = Solution().Deserialize(s)
# root.levelOrder()
# print('层序')
# ss = Solution().Serialize(root)
# print(ss)
JZ84 二叉树中和为某一值的路径(三) ▲
JZ84 二叉树中和为某一值的路径(三)
思路正确,否则就很难
本题没有时空复杂度限制,怎么简单怎么来
最简单的思路:两次先序遍历,第一次确定起点,第二次dfs找路径,就这么简单
每次定死一个起点,绝对不会有重复的 起点到每个结点都只算了一次
误区:
先序遍历到叶子节点 依次记录结点值,然后穷举所有路径 不可行,因为公共路径会被重复计算
from myutils.MyTree import *
'''
以每个节点作为起点 都试一次才行 (时间复杂度一样的 都O(n^2))
本题最大的好处在于没有限制 时空复杂度
'''
class Solution:
count = 0
def FindPath(self, root: TreeNode, sumv: int) -> int:
if not root: return 0
self.DFSPath(root, sumv)
self.FindPath(root.left, sumv)
self.FindPath(root.right, sumv)
return self.count
def DFSPath(self, root, sumv):
if sumv - root.val == 0: # 不需要到叶子 任意一个节点为0都行
Solution.count += 1
if root.left: self.DFSPath(root.left, sumv - root.val)
if root.right: self.DFSPath(root.right, sumv - root.val)
if __name__ == '__main__':
data = [1, 2, 3, 4, 5, 4, 3, '#', '#', -1]
k = 6
data = []
k = 0
#
# data = [2]
# k = 2
# data = [1, '#', 2, '#', 3, '#', 4, '#', 5]
# k = 3
#
# data = [10, 5, -3, 3, 2, '#', 11, 3, -2, '#', 1]
# k = 8
root = levelCreate(data)
count = Solution().FindPath(root, k)
print(count)
JZ86 在二叉树中找到两个节点的最近公共祖先 (TODO 递归解法还不懂)
JZ86 在二叉树中找到两个节点的最近公共祖先
from myutils.MyTree import *
class Solution:
def lowestCommonAncestor(self, root: TreeNode, o1: int, o2: int) -> int:
self.PathVals(root, o1, [])
self.PathVals(root, o2, [])
p1, p2 = self.path
for i in range(max(len(p1), len(p2))):
v1 = p1[i] if i<len(p1) else -1
v2 = p2[i] if i < len(p2) else -1
# print(v1, v2)
if v1!=v2:
return p1[i-1]
return root.val
path = []
def PathVals(self, root: TreeNode, o: int, path: list) -> list:
if not root: return
path.append(root.val)
if root.val == o:
self.path.append(path.copy())
return
if root.left: self.PathVals(root.left, o, path)
if root.right: self.PathVals(root.right, o, path)
path.pop(-1)
if __name__ == '__main__':
data = [3, 5, 1, 6, 2, 0, 8, '#', '#', 7, 4]
root = levelCreate(data)
o1, o2 = 5, 1
# o1, o2 = 2, 7
ans = Solution().lowestCommonAncestor(root, o1, o2)
print(ans)
1.3 队列 & 栈
JZ9 用两个栈实现队列
JZ9 用两个栈实现队列
水题,入栈1,弹出时先出栈到栈2即可
class Solution:
def __init__(self):
self.stack1 = []
self.stack2 = []
def push(self, node):
self.stack1.append(node) # 直接入栈
def pop(self):
if len(self.stack2) == 0:
while len(self.stack1) > 0:
self.stack2.append(self.stack1.pop(-1)) # 1出栈依次压入2
return self.stack2.pop(-1) # 2顺序正好1反 也就是2出栈顺序就是1进栈顺序
if __name__ == '__main__':
cmd = ["PSH1", "PSH2", "POP", "POP"]
cmd = ["PSH2", "POP", "PSH1", "POP"]
sol = Solution()
for c in cmd:
if 'PSH' in c:
sol.push(int(c[3:]))
else:
print(sol.pop(),end=' ')
JZ30 包含min函数的栈
JZ30 包含min函数的栈
- min方法 时间O(n)
class Solution:
def __init__(self):
self.data = []
def push(self, node):
self.data.append(node)
def pop(self):
return self.data.pop(-1)
def top(self):
return self.data[-1]
def min(self):
return min(self.data)
- min方法 时间O(1)
'''
本题难点,所有操作的时间复杂度都为1
当然包括寻找最小元素
'''
class Solution:
def __init__(self):
self.data = []
self.data_min = [] # 最小值栈 牺牲空间 保证min操作的时间为O(1)
def push(self, node):
self.data.append(node)
if len(self.data_min) == 0 or self.data_min[-1] > node:
self.data_min.append(node)
else:
self.data_min.append(self.data_min[-1]) # 继续当前最小的即可
# 最小的没出栈之前,min栈往上都是最小的那个
def pop(self):
self.data.pop(-1)
self.data_min.pop(-1) #两个栈一起pop (题目没有要求返回)
def top(self):
return self.data[-1]
def min(self):
return self.data_min[-1] # 没有出栈操作 正常返回
JZ31 栈的压入、弹出序列
JZ31 栈的压入、弹出序列
用"后面所有比我小的相对顺序一定是对应出栈序的逆序"这个结论,会超时
写代码判断,其实 直接手动模拟入栈出栈,是最快的
from typing import *
'''
其实没那么复杂 写代码直接模拟一下入栈出栈即可
'''
class Solution:
def IsPopOrder(self, pushV: List[int], popV: List[int]) -> bool:
stack = []
for i in pushV:
stack.append(i) # 入栈
# 看看是否需要弹栈
while len(stack) > 0 and stack[-1] == popV[0]:
stack.pop(-1)
popV.pop(0)
return len(stack) == 0
if __name__ == '__main__':
p1 = [1, 2, 3, 4, 5]
p2 = [4, 5, 3, 2, 1]
# p2 = [4, 3, 5, 1, 2]
p1 = [1]
p2 = [2]
# p1 = [1, 2, 3, 4, 5]
# p2 = [4, 3, 2, 6, 5]
p1 = [2, 1, 0]
p2 = [1, 2, 0]
ans = Solution().IsPopOrder(p1, p2)
print(ans)
JZ73 翻转单词序列
JZ73 翻转单词序列
# 每个单词单独原地反转+整体原地反转一次
class Solution:
def ReverseSentence(self , str: str) -> str:
str = str[::-1] #整体原地反转
return ' '.join(ss[::-1] for ss in str.split(' ')) #每个单词单独反转后空格连接
if __name__ == '__main__':
ss = "nowcoder. a am I"
ans =Solution().ReverseSentence(ss)
print(ans)
JZ59 滑动窗口的最大值 (# 双队列法:TODO)
JZ59 滑动窗口的最大值
- 直接暴力也能过
class Solution:
def maxInWindows(self, num: List[int], size: int) -> List[int]:
if size < 1: return []
ans = []
for i in range(size - 1, len(num)):
ans.append(max(num[i - size + 1:i + 1]))
return ans
2、算法
2.1 搜索算法
JZ53 数字在升序数组中出现的次数
JZ53 数字在升序数组中出现的次数
要求时间复杂度 O(logn) 就必须用二分查找了
得会写标准的二分查找才行,也就是查找失败要返回应该插入的位置下标
这样两次二分查找的差值就是了
from typing import *
class Solution:
# 数组data里找k的下标位置 失败就返回应该插入的位置 二分查找 保证时间复杂度log2N
def binarySearch(self,data,k):
l,r = 0,len(data)-1 #l,r是严格的合法下标上下限(i,j也是合法下标)
while l<=r: #必须有等号 保证查找失败时 l>r即l=r+1 此时l就是应该插入的位置下标
mid = (l+r)//2 #注意//整除
if data[mid] == k: return mid
elif k < data[mid]: r = mid -1
else: l = mid + 1
return l # 查找失败时 k值应该插入的位置
def GetNumberOfK(self , data: List[int], k: int) -> int:
return self.binarySearch(data,k+0.5) - self.binarySearch(data,k-0.5)
if __name__ == '__main__':
data = [1, 2, 3, 3, 3, 3, 4, 5]
k = 3
print(Solution().GetNumberOfK(data,k))
JZ4 二维数组中的查找
JZ4 二维数组中的查找
- 方法一 直接暴力
class Solution:
def Find(self, target: int, array: List[List[int]]) -> bool:
for arr in array:
for i in arr:
if i == target:
return True
return False
- 方法二,左上角最小元素处开始走(找) [逻辑有点太复杂]
'''
方法一 暴力
'''
from typing import *
class Solution:
def Find(self, target: int, array: List[List[int]]) -> bool:
w, h = len(array[0]), len(array)
if w == 0 or h == 0: return False
i, j = 0, 0
flag = 0 # 0横着走 1竖着走
while True:
if array[i][j] == target:
return True
elif array[i][j] < target:
if flag == 0: # 横着走比当前大
if j + 1 < w:
j += 1 # 继续横着走
else:
flag = 1
else: # 竖着走比当前大
if i + 1 < h: # 继续往下
i += 1
else:
return False # 先横着走 然后竖着走比最下面还要大 肯定没有
else: # target要小
if flag == 0: # 横着走小于当前值
if i + 1 < h: # 竖着往下走
i += 1
flag = 1
else:
return False
else: # 竖着走小于当前值
if j - 1 >= 0:
j -= 1 # 横着退也算竖着走
else:
return False
return True
if __name__ == '__main__':
k = 7
data = [[1, 2, 8, 9], [2, 4, 9, 12], [4, 7, 10, 13], [6, 8, 11, 15]]
data = [[]]
k = 2
data = [[1, 1]]
ans = Solution().Find(k, data)
print(ans)
- 方法三,最牛 其实从最左下角开始走 逻辑变得非常非常简单 ★
每个元素是以其为右下顶点组成矩形区域内的最大值
因此从最下角开始走,比target小,只能往右,比target大只能往上(开始就是左边来的)
class Solution:
def Find(self, target: int, array: List[List[int]]) -> bool:
w, h = len(array[0]), len(array)
# if w == 0 or h == 0: return False # 天然保证了
i, j = h-1, 0
while True:
if j>=w or i<0: return False
if array[i][j] == target: return True
elif array[i][j] < target: j+=1 # 比target小,只能往右(找更大)
else: i -= 1 # 比target要大 只能往上(找更小 左边刚找过)
JZ11 旋转数组的最小数字
JZ11 旋转数组的最小数字
找变化,也差不多就是O(n)了,除了二分,其他也都差不多
class Solution:
def minNumberInRotateArray(self , arr: List[int]) -> int:
flag = 1 if arr[0]<=arr[1] else 0 #注意等号
for i in range(1,len(arr)):
flagt = 1 if arr[i-1]<=arr[i] else 0 #注意等号
if flag == 1 and flagt==0: return arr[i]
elif flag == 0 and flagt==1: return arr[i-1]
if flag == 0: return arr[-1] # 完全递减(不增)
else: return arr[0] # 完全递增(不减)
JZ38 字符串的排列 (TODO)
JZ38 字符串的排列
- 方法一:使用内置api: itertools.permutations
注意用set去重
import itertools
class Solution:
def Permutation(self , str: str) -> List[str]:
ans = set() # 集合用来去重 创建空集合得用set() {}是创建空字典的
for s in itertools.permutations(str):
ans.add(''.join(i for i in s))
return list(ans)
-方法二: 本题本意应该是让你自己实现类似的permutations功能,所以老老实实写一遍吧
JZ44 数字序列中某一位的数字
JZ44 数字序列中某一位的数字
- 方法一,直接找规律
class Solution:
def findNthDigit(self, n: int) -> int:
if n<10: return n # 1
elif n<10+2*90: # 2
a = (n-10)/2
b = (n-10)%2
return int(str(10+a)[b])
elif n<10+2*90+3*900: # 3
a = (n-(10+2*90))/3
b = (n-(10+2*90))%3
return int(str(100+a)[b])
elif n < 10+2*90+3*900+4*9000: # 4
a = (n-(10+2*90+3*900))/4
b = (n-(10+2*90+3*900))%4
return int(str(1000 + a)[b])
elif n < 10+2*90+3*900+4*9000+5*90000: # 5
a = (n-(10+2*90+3*900+4*9000))/5
b = (n-(10+2*90+3*900+4*9000))%5
return int(str(10000 + a)[b])
elif n < 10+2*90+3*900+4*9000+5*90000+6*900000: # 6
a = (n-(10+2*90+3*900+4*9000+5*90000))/6
b = (n-(10+2*90+3*900+4*9000+5*90000))%6
return int(str(100000 + a)[b])
elif n < 10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000: # 7
a = (n-(10+2*90+3*900+4*9000+5*90000+6*900000))/7
b = (n-(10+2*90+3*900+4*9000+5*90000+6*900000))%7
return int(str(1000000 + a)[b])
elif n < 10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000+8*90000000: # 8
a = (n-(10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000))/8
b = (n-(10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000))%8
return int(str(10000000 + a)[b])
elif n < 10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000+8*90000000+9*900000000: # 9
a = (n-(10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000+8*90000000))/9
b = (n-(10+2*90+3*900+4*9000+5*90000+6*900000+7*9000000+8*90000000))%9
return int(str(100000000 + a)[b])
def findN():
ans = 10
mul = 90
print('1*', ans, end=' ')
for i in range(2, 10):
ans += i * mul
print('+', i, '*', mul, end=' ')
mul *= 10
print('=', ans)
print(ans / (pow(10, 9)))
# 说明数字最大排到了 9 位
'''
1* 10 + 2 * 90 + 3 * 900 + 4 * 9000 + 5 * 90000 + 6 * 900000 + 7 * 9000000 + 8 * 90000000 + 9 * 900000000 = 8888888890
8.88888889
'''
if __name__ == '__main__':
n = 1000000000
ans = Solution().findNthDigit(n)
print(ans)
- 方法二 : 将方法一改成循环写法即可
class Solution:
def findNthDigit(self, n: int) -> int:
if n < 10: return n
top = 10
for N in range(2, 10): # N位数
if n < top + N * 9 * pow(10, N - 1):
a = (n - top) / N
b = (n - top) % N
return int(str(pow(10, N - 1) + a)[b])
top += N * 9 * pow(10, N - 1)
if __name__ == '__main__':
n = 1000000000
ans = Solution().findNthDigit(n)
print(ans)
2.2 动态规划
参考博文: 算法笔记11.2~11.6 最大连续子序列和 最长不降子序列(LIS) 最长公共子序列(LCS) 最大回文子串 DAG最长路
JZ42 连续子数组的最大和
JZ42 连续子数组的最大和
package cn.whu.jz.JZ42连续子数组的最大和;
public class JZ42 {
public int FindGreatestSumOfSubArray(int[] array) {
int[] dp = new int[array.length];
dp[0] = array[0];
int max = dp[0];
for (int i = 1; i < array.length; i++) {
dp[i] = Math.max(dp[i - 1] + array[i], array[i]);
if (dp[i] > max) max = dp[i];
}
return max;
}
public static void main(String[] args) {
int array[] = {1, -2, 3, 10, -4, 7, 2, -5};
// int array[] = {2};
// int array[] = {-10};
int ans = new JZ42().FindGreatestSumOfSubArray(array);
System.out.println(ans);
}
}
上面时间空间都是O(n).
其实仔细观察代码,不难发现,每次dp[i]都只会用到前一次的dp[i-1],则空间可以进一步压缩
package cn.whu.jz.JZ42连续子数组的最大和;
public class JZ42_1 {
//观察代码可以发现 每次dp[i]都只需要dp[i-1]因此 不需要开辟dp数组
public int FindGreatestSumOfSubArray(int[] array) {
int sum = array[0];
int max = array[0];
for (int i = 1; i < array.length; i++) {
sum = Math.max(sum + array[i], array[i]);
if (sum > max) max = sum;
}
return max;
}
public static void main(String[] args) {
int array[] = {1, -2, 3, 10, -4, 7, 2, -5};
// int array[] = {2};
// int array[] = {-10};
int ans = new JZ42_1().FindGreatestSumOfSubArray(array);
System.out.println(ans);
}
}
JZ85 连续子数组的最大和(二)
JZ85 连续子数组的最大和(二)
和上面差不多,但此处要求序列本身,因此要一些辅助变量记录最大值时序列状态
为了空间O(1),.定义了许多标记变量
package cn.whu.jz.JZ85连续子数组的最大和2;
import java.util.Arrays;
public class JZ85 {
public int[] FindGreatestSumOfSubArray(int[] array) {
int sum = array[0];
int max = array[0];
int maxL = 1;
int L = 1;
int ansI = 0;
for (int i = 1; i < array.length; i++) {
if (array[i] + sum >= array[i]) {//不增不减 连上 因为要最长
sum = array[i] + sum;
L++;
} else {
sum = array[i];
L = 1;
}
if (sum > max || (sum == max && L > maxL)) {
max = sum;
maxL = L;
ansI = i;
}
}
return Arrays.copyOfRange(array, ansI - maxL + 1, ansI + 1);
}
public static void main(String[] args) {
int array[] = {1, 2, -3, 4, -1, 1, -3, 2};
int[] ans = new JZ85().FindGreatestSumOfSubArray(array);
System.out.println(Arrays.toString(ans));
}
}
JZ69 跳台阶
JZ69 跳台阶
水题,就斐波那契数列,甚至连剪枝都不用,数据量太小
public class Solution {
//水题 就是斐波那契
public int jumpFloor(int n) {
if(n<=1) return 1;
return jumpFloor(n-1)+jumpFloor(n-2);
}
}
时间 O(2^n)
数据量大的话,可能就得剪枝了 比如 第100项
public class Solution {
//水题 就是斐波那契
static int[] fac = new int[50];
public int jumpFloor(int n) {
if(n<=1) return 1;
if(fac[n]==0) fac[n] = jumpFloor(n-1)+jumpFloor(n-2);//仅仅此时需要递归
return fac[n];//最后退栈返回的就是 n!
}
}
JZ10 斐波那契数列
JZ10 斐波那契数列
还是极其水的斐波那契,换一种方式写吧
public class Solution {
public int Fibonacci(int n) {
int a=1,b=1,c=0;
if(n<=2) return 1;
for(int i=3;i<=n;i++){
c = a+b;
a = b;
b = c;
}
return c;
}
}
JZ71 跳台阶扩展问题
JZ71 跳台阶扩展问题
比斐波那契还要水,直接2^(n-1)
public int jumpFloorII(int n) {
return 1<<(n-1);
}
注意Math.pow(double,double) java不能强转为int,所以用1< JZ19 正则表达式匹配 直接for循环 字符串匹配 失败,太复杂了 就不贴了 整理一下,也还好(初始化可以省略 直接就在二重循环里进行了) JZ63 买卖股票的最好时机(一) 牛客的数据着实有点弱了 JZ70 矩形覆盖 本题n只到38,可以用递归偷懒 JZ47 礼物的最大价值 相当DP就不难了,很简单的DP Tips: 外围填充0,边界也就不用特殊处理 (dp下标都从1开始也就行了) JZ48 最长不含重复字符的子字符串 类似最长回文子串的写法,内存竟然超了。字符串很长时,二维的boolean数组可能确实吃不消。 直接去看题解,唉,看懂很容易,但是自己想好难啊。 1、双指针法,左右指针维持一个窗口 JZ46 把数字翻译成字符串 dp做得多了,一旦想到了,就很简单了。 JZ12 矩阵中的路径 就是简单DFS,好久没写了,一些细节都忽略了,调试了好几次 优化一下代码,太乱了(代码可能简洁一点,但是效率会低一点) ★优化1:去掉了visited数组,不用数组标记是否访问过,浪费空间不说,还得每次重置为false,也大大浪费了时间。直接访问后改为非法值(得有非法值),退栈时再改回来,巧夺天工啊,省时省力 JZ13 机器人的运动范围 不难也是简单DFS JZ3 数组中重复的数字 JZ51 数组中的逆序对 开始误认为直接插入排序时间是O(nlogn).后来猛然想起来,由于元素移动次数还是那么多,所以时间还是O(n2). 空间O(1) 时间O(n2) 。 不过竟然也过了,牛客数据有点弱啊 不过收获挺大的,好久没写二分了,尤其返回插入位置,出了3个意想不到的错误 error1: mid = (array[l] + array[r]) / 2 => correct: mid = (l+r)/2 想要O(nlogn)的排序只有归并、堆排和快排了, 以下是讨论模块直接copy过来的,主要为了把一些关键强调一下 (a) 把长度为4的数组分解成两个长度为2的子数组; 过程:先把数组分割成子数组,先统计出子数组内部的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中,还需要对数组进行排序。如果对排序算法很熟悉,我们不难发现这个过程实际上就是归并排序。参考代码如下: JZ40 最小的K个数 一眼望去堆排序,直接上堆就是了 JZ41 数据流中的中位数 中位数怎么用堆呢?又不是最大最小值。傻-》两个堆不就行了 前一半元素维护一个大根堆 JZ65 不用加减乘除做加法 位运算做加法,做过就很简单。 所以=》+用异或代替 但是直接异或少加了进位=》还得加上进位位,也就是上一位的相与结果=》于是还得再和每上一位相与结果进行异或=》不断重复,直到进位位为0 JZ15 二进制中1的个数 本题很简单: 优化1:java提供了 >>> 无符号右移动。无论符号位(无论正负)是啥,高位都补0,也就是把数强制看成无符号数进行逻辑右移。 技巧优化,或者说直接差每一位 JZ16 数值的整数次方 注意此题很简单,指数是int类型,没有小数,不存在开方问题 JZ56 数组中只出现一次的两个数字 本题用到一个很不起眼但是很有用的公式: n^n=0 一个数和自己异或得0. // n^n=0 JZ64 求1+2+3+…+n JZ29 顺时针打印矩阵 细节有点麻烦,得慢慢调,不那么简单。 JZ61 扑克牌顺子 JZ67 把字符串转换成整数(atoi) JZ20 表示数值的字符串 不过一个加一个正则,总能过。 唉 JZ66 构建乘积数组 先求下三角每行乘积,再求上三角每行乘积,最后每行前一半和后一半乘积相乘即可 JZ50 第一个只出现一次的字符 JZ5 替换空格 太水了 JZ21 调整数组顺序使奇数位于偶数前面(一) JZ39 数组中出现次数超过一半的数字 难点在于空间要求O(1) 基准base,次数t JZ43 整数中1出现的次数(从1到n整数中1出现的次数) 之前刷PAT时刷到过,看了下题解,秒懂,就是要分析规律 其实用不着这么麻烦,用C++写可能还简单点,正常遍历即可 JZ45 把数组排成最小的数 清晰地记得做过,就是条件排序,s1+s2 或者: JZ49 丑数 //别想太多了,核心就是去重,但是数据范围太大咋办? 用java的HashMap去重啊~ 注意:数字得用Long类型,因为int*5 可能会溢出 JZ74 和为S的连续正数序列 先穷举,也能过 因为剪枝的存在,时间效率其实也还不错 JZ57 和为S的两个数字 有了上题的基础,这题就很简单了,直接双指针 其实本题Hash也行,时间也是O(2*n),但是消耗了空间 深刻体会到map确实好用 JZ58 左旋转字符串 经典老题,408也出现过,空间O(n)没难度,空间O(1)就三次原地逆置了 JZ62 孩子们的游戏(圆圈中最后剩下的数) 更牛: 假设一开始只有n=1 那么last必然等于0,然后直接用上面两列推导出的公式不断往回推导即可。纯数学约瑟夫环问题 JZ75 字符流中第一个不重复的字符 JZ14 剪绳子 简单DP,但是没想到 JZ81 调整数组顺序使奇数位于偶数前面(二) 时间复杂度 O(n), JZ83 剪绳子(进阶版) 直接这么写会溢出,中间没法取模啊,于是自己求幂,O(logn),必然快速幂了 悲剧的是,单纯快速幂还是会溢出,还得写一个不断%mod的快速乘法 JZ17 打印从1到最大的n位数JZ19 正则表达式匹配 (HARD)
只能用DP了package cn.whu.jz.JZ19正则表达式匹配;
public class JZ19 {
public boolean match(String str, String pattern) {
int l1 = str.length(), l2 = pattern.length();
boolean[][] dp = new boolean[l1 + 1][l2 + 1];
//dp[i][j] 指的是str前i前缀 与 pattern前j前缀 是否匹配 (是长度 不是下标 对应最大下标为i-1 j-1)
//初始化边界
dp[0][0] = true;//两空直接匹配
dp[0][1] = false;//其实就是默认的
for (int j = 2; j <= l2; j++) {
if (pattern.charAt(j - 1) == '*') {//注意i,j是长度 对应下标-1
dp[0][j] = dp[0][j - 2];//不出现才行
}//否则直接默认0就行了
}
for (int i = 1; i <= l1; i++) {
for (int j = 0; j <= l2; j++) {
if (j == 0) {
if (i == 0) dp[i][j] = true;
} else {
if (pattern.charAt(j - 1) != '*') {//非'*'
if (pattern.charAt(j - 1) == str.charAt(i - 1) || pattern.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
}
} else {//是'*'
if (j >= 2) {
dp[i][j] |= dp[i][j - 2];//或操作没事儿 想看不出现能不能匹配上
}
if (j >= 2 && pattern.charAt(j - 2) == '.' || pattern.charAt(j - 2) == str.charAt(i - 1)) {
//*前面一个和当前匹配 X*与XX
dp[i][j] |= dp[i - 1][j];//注意str这一个可以忽略了,被*匹配了 (i-1不是j-1)
//i-1或者j-1前面循环已经都算出来了
//用|是因为万一前面不出现时为1了呢 (有一种匹配为1就行 所以用|可以无限尝试)
}
//其他各种不匹配默认值为0即可
}
}
}
}
return dp[l1][l2];
}
public static void main(String[] args) {
// String str = "ab";
// String pattern = ".*ab";
// "ab",".*ab" "a", "a"
boolean match = new JZ19().match("ab",".*ab");
System.out.println(match);
}
}
package cn.whu.jz.JZ19正则表达式匹配;
public class JZ19_1 {
public boolean match(String str, String pattern) {
int l1 = str.length(), l2 = pattern.length();
boolean[][] dp = new boolean[l1 + 1][l2 + 1];
//dp[i][j] 指的是str前i前缀 与 pattern前j前缀 是否匹配 (是长度 不是下标 对应最大下标为i-1 j-1)
for (int i = 0; i <= l1; i++) {
for (int j = 0; j <= l2; j++) {
if (j == 0) {
if (i == 0) dp[i][j] = true;
} else {
if (pattern.charAt(j - 1) != '*') {//非'*'
if (i>0 && (pattern.charAt(j - 1) == str.charAt(i - 1) || pattern.charAt(j - 1) == '.'))
dp[i][j] = dp[i - 1][j - 1];
} else {//是'*'
if (j >= 2) dp[i][j] |= dp[i][j - 2];//或操作没事儿 想看不出现能不能匹配上
if (i>0 && j >= 2 && (pattern.charAt(j - 2) == '.' || pattern.charAt(j - 2) == str.charAt(i - 1)))
dp[i][j] |= dp[i - 1][j];
}
}
}
}
return dp[l1][l2];
}
public static void main(String[] args) {
// "ab",".*ab" "a", "a"
boolean match = new JZ19_1().match("ab",".*ab");
System.out.println(match);
}
}
JZ63 买卖股票的最好时机(一)
时间O(n^2)不满足要求public class JZ63 {
public int maxProfit (int[] prices) {
int[][] dp = new int[prices.length][prices.length];
int max = 0;
for(int i=0;i<prices.length;i++){
for(int j=i+1;j<prices.length;j++){
dp[i][j]=prices[j]-prices[i];
if(dp[i][j]>max) max=dp[i][j];
}
}
return max;
}
public static void main(String[] args) {
int profit = new JZ63().maxProfit(new int[]{8, 9, 2, 5, 4, 7, 1});
System.out.println(profit);
}
}
public class JZ63 {
//贪心即可,一趟遍历 min维护当前最小值 max维护当前最大值 当前值-min更新max
public int maxProfit(int[] prices) {
//int min = 100000;
int min = Integer.MAX_VALUE;
int max = 0;
for (int i = 0; i < prices.length; i++) {
if (prices[i] < min) min = prices[i];
if (prices[i] - min > max) max = prices[i] - min;
}
return max;
}
public static void main(String[] args) {
int profit = new JZ63().maxProfit(new int[]{8, 9, 2, 5, 4, 7, 1});
System.out.println(profit);
}
}
JZ70 矩形覆盖
长度是n 高度是2
所有想法都失败了 找规律发现竟然仍然时斐波那契
于是脑中就有了 递推思路了
dp[n]的话 可以是dp[n-1]+1块竖着的
也可以是dp[n-2]+2块横着的 (不能两块竖着 否则和上面情况重复了)
于是便有了: dp[n]=dp[n-1]+dp[n+1]
初始: dp[0]=0 dp[1]=1 dp[2]=2 dp[3]=3 dp[4]=5
public int rectCover(int target) {
int a = 0, b = 1, t = 0;
for (int i = 1; i <= target; i++) {
t = a + b;
a = b;
b = t;
}
return t;
}
public int rectCover(int target) {
if(target<=3) return target;//n=0,1,2,3 时无递归 递归出口设置大点没事儿
return rectCover(target-1)+rectCover(target-2);
}
JZ47 礼物的最大价值
状态转移方程非常简单:dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]) + grid[i][j];
public int maxValue(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m + 1][n + 1];//下标1开始 外围0填充
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]) + grid[i][j];
}
}
return dp[m][n];
}
JZ48 最长不含重复字符的子字符串
2、用一个Hash表记录字符出现的次数
3、滑动窗口,保证窗口内元素出现此处均为1,这就需要再右边第一次进来重复元素后,左指针慢慢右移,直到新重复元素次数减为1public int lengthOfLongestSubstring(String s) {
int[] hash = new int[128];//ascii只可能有128种 默认值均为0
int p1 = 0, p2 = 0;
int max = 0;
for (p2 = 0; p2 < s.length(); p2++) {
hash[s.charAt(p2)]++;
while (hash[s.charAt(p2)] > 1) {
hash[s.charAt(p1)] -= 1;
p1++;
}
if (p2 - p1 + 1 > max) max = p2 - p1 + 1;
}
return max;
}
JZ46 把数字翻译成字符串
本题刚读完,就立刻想到了矩形覆盖那题,立刻就想到了斐波那契数列,于是就有戏了。调了一下,解决了。
public class JZ46 {
//突然想到了矩形覆盖那题,立刻就想到了斐波那契额 好像有戏
// dp[k]=dp[k-1] or dp[k-1]+dp[k-2]
public int solve(String str) {
char[] chars = str.toCharArray();
if(chars[0]=='0') return 0;
if(chars.length==1) return 1;
int[] dp = new int[90];
dp[0] = 1;
if (chars[1] != '0' && (chars[0] - '0') * 10 + (chars[1] - '0') <= 26) dp[1] = 2;
else dp[1] = 1;
for (int i = 2; i < chars.length; i++) {
if(chars[i]=='0'){
if(chars[i-1]=='0'||chars[i-1]>'2') return 0;//前面接不上
else dp[i]=dp[i-2];//前面接上了
}else {
if( (chars[i-1]!='0') && (chars[i-1]-'0')*10+(chars[i]-'0')<=26) dp[i]=dp[i-1]+dp[i-2];
else dp[i] = dp[i-1];
}
}
return dp[chars.length-1];
}
public static void main(String[] args) {
// "12" "31717126241541717"
// 72910721221427251718216239162221131917242
int solve = new JZ46().solve("72910721221427251718216239162221131917242");
System.out.println(solve);
}
}
JZ12 矩阵中的路径
package cn.whu.jz.JZ12矩阵中的路径;
import java.util.Arrays;
public class JZ12 {
public boolean hasPath(char[][] matrix, String word) {
int m = matrix.length, n = matrix[0].length;//m行 n列
visited = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == word.charAt(0)) {
//每次遍历之前,visited置为false // 不能让前一次的visit影响下一次啊
for (boolean[] vis : visited) Arrays.fill(vis, false);
if (dfs(matrix, word, i, j, 0)) return true;
}
}
}
return false;
}
int[] dx = {-1, 1, 0, 0};
int[] dy = {0, 0, -1, 1};
boolean judge(char[][] matrix, char c, int x, int y) {
if (x < 0 || x >= matrix.length || y < 0 || y >= matrix[0].length) return false;
if (matrix[x][y] != c || visited[x][y]) return false;
return true;
}
boolean[][] visited = null;
boolean dfs(char[][] matrix, String word, int i, int j, int k) {
//System.out.print(matrix[i][j]+" ");
visited[i][j] = true;//访问
if (k == word.length() - 1) return true;
// 上下左右的走
for (int c = 0; c < 4; c++) {
if (judge(matrix, word.charAt(k + 1), i + dx[c], j + dy[c])) {
//千万注意 此处也不能直接return,true才能return 否则多个方向都有可能,也只会尝试一个方向
if (dfs(matrix, word, i + dx[c], j + dy[c], k + 1)) return true;
}
}
//否则退栈时需要取消本次访问啊
visited[i][j] = false;//只是本分支不行,下个可行分支可能要经过这个节点。
return false;//上面4个方向都走不了 此分支只能false
}
public static void main(String[] args) {
/*char[][] matrix = {{'a','b','c','e'},{'s','f','c','s'},{'a','d','e','e'}};
String word = "abcced";
word = "abcb";
word = "see";*/
char[][] matrix = {{'A', 'B', 'C'},{'B', 'E', 'D'},{'F', 'G', 'G'}};
for (char[] chars : matrix) {
for (char aChar : chars) System.out.print(aChar+" ");
System.out.println();
}
String word = "ABCDEBF";
boolean b = new JZ12().hasPath(matrix, word);
System.out.println(b);
}
}
后验:直接无脑dfs,dfs内先判断是否合法。代码会精简许多public boolean hasPath(char[][] matrix, String word) {
int m = matrix.length, n = matrix[0].length;//m行 n列
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (dfs(matrix, word, i, j, 0)) return true;
return false;
}
boolean dfs(char[][] matrix, String word, int i, int j, int k) {
if (i < 0 || i >= matrix.length || j < 0 || j >= matrix[0].length|| matrix[i][j]!=word.charAt(k)) return false;
//System.out.print(matrix[i][j]+" ");
if (k == word.length() - 1) return true;
char tmp = matrix[i][j];
matrix[i][j] = '*';// 特殊不可能出现的字符 (这个条件得先知道)
// 上下左右的走
boolean res = dfs(matrix,word,i+1,j,k+1) ||
dfs(matrix,word,i-1,j,k+1) ||
dfs(matrix,word,i,j+1,k+1) ||
dfs(matrix,word,i,j-1,k+1);
matrix[i][j] = tmp;//退栈时再改回来
return res;//上面不能直接返回了 否则来不及还原matrix[i][j] = tmp
}
JZ13 机器人的运动范围
package cn.whu.jz.JZ13机器人的运动范围;
public class JZ13 {
int[][] mat = null;
int rows,cols,count;
public int movingCount(int threshold, int rows, int cols) {
this.mat = new int[rows][cols];
this.rows = rows;
this.cols = cols;
dfs(threshold,0,0);
return this.count;
}
int Sum(int r,int c){
int sum =0;
while (r!=0){
sum += r%10;
r /= 10;
}
while (c!=0){
sum += c%10;
c /= 10;
}
return sum;
}
void dfs(int threshold,int r,int c){
if(r<0||r>=this.rows||c<0||c>=this.cols||Sum(r,c)>threshold||mat[r][c]==1) return;
this.count++;
mat[r][c]=1;//访问过的不需要访问了 反正也是找连通域
dfs(threshold,r-1,c);
dfs(threshold,r+1,c);
dfs(threshold,r,c+1);
dfs(threshold,r,c-1);
}
public static void main(String[] args) {
System.out.println(new JZ13().movingCount(1,2,3));
System.out.println(new JZ13().movingCount(0,1,3));
System.out.println(new JZ13().movingCount(10,1,100));
System.out.println(new JZ13().movingCount(5,10,10));
}
}
JZ3 数组中重复的数字
水题 public int duplicate (int[] numbers) {
int N = numbers.length;
int[] Hash = new int[N];
for (int i : numbers) {
if(i>=N) return -1;
if(Hash[i]>0) return i;
Hash[i]++;
}
return -1;
}
JZ51 数组中的逆序对
public int InversePairs(int [] array) {
int sum = 0;
for(int i=1;i<array.length;i++){
int l=0,r=i-1;//开始不能包括i本身
while (l<=r) {
int mid = (l+r) / 2;//竟然写成了 mid = (array[l] + array[r]) / 2
if (array[i] > array[mid]) r= mid-1; //得逆序排序 竟然写成了 array[i] > mid
else l = mid+1; //题目保证不存在重复
}
sum = (sum+l)%1000000007;//插入位置就是左边有几个比他小的 // 还必须写l了
//System.out.print(l+" ");
int t = array[i];
for(int j=i;j>l;j--) array[j]=array[j-1];//j>l竟然写成j>i了
array[l]=t;
}
return sum%1000000007;
}
error2: array[i] > mid => correct: array[i] > array[mid]
error3: for(int j=i;j>i;j–) => correct: for(int j=i;j>l;j–)
归并可以改造成功。讨论里的题解非常不错
思路分析:
看到这个题目,我们的第一反应是顺序扫描整个数组。每扫描到一个数组的时候,逐个比较该数字和它后面的数字的大小。如果后面的数字比它小,则这两个数字就组成了一个逆序对。假设数组中含有n个数字。由于每个数字都要和O(n)这个数字比较,因此这个算法的时间复杂度为O(n^2)。
我们以数组{7,5,6,4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候,我们不拿ta和后面的每一个数字作比较,否则时间复杂度就是O(n^2),因此我们可以考虑先比较两个相邻的数字。
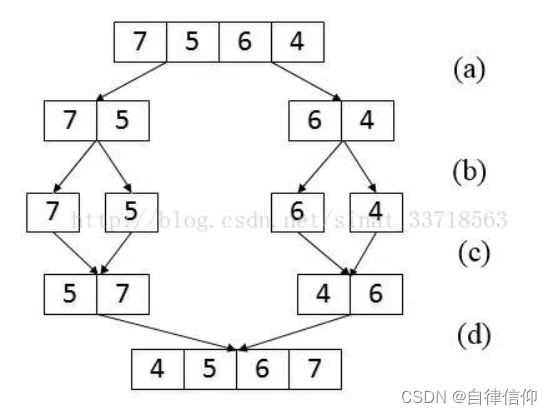
(b) 把长度为2的数组分解成两个成都为1的子数组;
© 把长度为1的子数组 合并、排序并统计逆序对 ;
(d) 把长度为2的子数组合并、排序,并统计逆序对;
在上图(a)和(b)中,我们先把数组分解成两个长度为2的子数组,再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组,一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5,因此(7,5)组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对(6,4)。由于我们已经统计了这两对子数组内部的逆序对,因此需要把这两对子数组 排序 如上图(c)所示, 以免在以后的统计过程中再重复统计。
接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图如下图所示。
我们先用两个指针分别指向两个子数组的末尾,并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字,则构成逆序对,并且逆序对的数目等于第二个子数组中剩余数字的个数,如下图(a)和(c)所示。如果第一个数组的数字小于或等于第二个数组中的数字,则不构成逆序对,如图b所示。每一次比较的时候,我们都把较大的数字从后面往前复制到一个辅助数组中,确保 辅助数组(记为copy) 中的数字是递增排序的。在把较大的数字复制到辅助数组之后,把对应的指针向前移动一位,接下来进行下一轮比较。

import java.util.Arrays;
public class JZ51_merge_finally {
public int InversePairs(int [] array) {
int[] copy = Arrays.copyOf(array, array.length);
return merge(array,copy,0,array.length-1);//是下标 千万注意 length-1
}
// 拆分出来好理解
int merge(int[] array,int[] copy,int l,int r){
if(l>=r) return 0;
int mid = (l+r)/2;
int lnum = merge(array,copy,l,mid);
int rnum = merge(array,copy,mid+1,r);
int i=mid,j=r,res=0,k=r;
while (i>=l&&j>=mid+1&&k>=l){//l~mid 和 mid+1~r
if(array[i]>array[j]) {
copy[k--]=array[i--];
res=(res+(j-mid))%1000000007;//不是简单+1 逆序对的数目等于第二个子数组中剩余数字的个数 array[i]比我大 那么比我前面的都大
} else copy[k--]=array[j--];
}
while (i>=l) copy[k--]=array[i--];
while (j>=mid+1) copy[k--]=array[j--];
// 排好序 覆盖回来 防止重复计算
for(int x=l;x<=r;x++) array[x]=copy[x];
return (lnum+rnum+res)%1000000007;//开始左右为空返回0 没事儿 后面就累加上了
}
public static void main(String[] args) {
JZ51_merge_finally t = new JZ51_merge_finally();
System.out.println(t.InversePairs(new int[]{1,2,3,4,5,6,7,0}));
System.out.println(t.InversePairs(new int[]{1,2,3}));
System.out.println(t.InversePairs(new int[]{6,5,4,3,2,1}));
System.out.println(t.InversePairs(new int[]{6,5,3,4,2,1}));
System.out.println(t.InversePairs(new int[]{6,5,3,4,2,1}));
System.out.println(t.InversePairs(new int[]{1,2,3,4,5,6,-1,-2,-3}));
int[] arr1 = {364,637,341,406,747,995,234,971,571,219,993,407,416,366,315,301,601,650,418,355,460,505,360,965,516,648,727,667,465,849,455,181,486,149,588,233,144,174,557,67,746,550,474,162,268,142,463,221,882,576,604,739,288,569,256,936,275,401,497,82,935,983,583,523,697,478,147,795,380,973,958,115,773,870,259,655,446,863,735,784,3,671,433,630,425,930,64,266,235,187,284,665,874,80,45,848,38,811,267,575};
System.out.println(t.InversePairs(arr1));
}
}
JZ40 最小的K个数
注意0下标不能用import java.util.ArrayList;
public class JZ40 {
//最小的k个数,一眼望去堆排序
public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
ArrayList<Integer> ans = new ArrayList<>();
if(k==0) return ans;
heap = new int[k + 1];//堆的下标1开始
for (int i = 0; i < k; i++) heap[i + 1] = input[i];//初始堆
for (int i = k / 2; i >= 1; i--) down(i);//建立堆 注意范围,下坠到根1
for (int i = k; i < input.length; i++) {//前面k个(0~k-1)不用管了 后面len-k个慢慢是
if (input[i] < heap[1]) {
heap[1] = input[i];
down(1);
}
}
for (int i = 1; i <= k; i++) ans.add(heap[i]);
return ans;
}
int[] heap = null;//大根堆
// 下坠 从i开始下坠 建堆要用 以后更新都是根1开始下坠
void down(int i) {
int j = i * 2;
while (j < heap.length) {//heap.length=k+1
if (j + 1 < heap.length && heap[j + 1] > heap[j]) j = j + 1;
if (heap[j] > heap[i]) {//需要调整
int t = heap[i];
heap[i] = heap[j];
heap[j] = t;
i = j;
j = i * 2;
} else break;
}
}
//不需要插入 也就没有上浮操作了
public static void main(String[] args) {
JZ40 t = new JZ40();
ArrayList<Integer> list1 = t.GetLeastNumbers_Solution(new int[]{4, 5, 1, 6, 2, 7, 3, 8}, 4);
System.out.println(list1);
int[] inputs = {4, 5, 1, 6, 2, 7, 3, 8};
int k = 0;
System.out.println(t.GetLeastNumbers_Solution(inputs,k));
}
}
PriorityQueue 建立大根堆后,保证了每次出队的都是堆顶最大值
自己查API文档很容易看懂,或者参考这篇博客 public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
ArrayList<Integer> ans = new ArrayList<>();
if(k==0||input.length==0) return ans;
PriorityQueue<Integer> heap = new PriorityQueue<>(((o1, o2) -> o2.compareTo(o1)));//大根堆
for(int i=0;i<k;i++) heap.offer(input[i]);
for(int i=k;i<input.length;i++){
if(input[i]<heap.peek()){
heap.poll();//删堆顶
heap.offer(input[i]);//新的入堆
}
}
while (!heap.isEmpty()) ans.add(heap.poll());
return ans;
}
JZ41 数据流中的中位数
int[] data = new int[1010];
int n = 0;
public void Insert(Integer num) {
data[n++]=num;
Arrays.sort(data,0,n);
}
public Double GetMedian() {
if(n%2==0) return (data[n/2]+data[n/2-1])/2.0;
return data[n/2]*1.0;
}
后一般元素维护一个小根堆
大顶堆 比 小顶堆 元素多一个 或者二者相等
…
奇数直接peek大顶堆
偶数 两个堆peek取平均
…
每次新元素进来,先进大根堆,再将大根堆顶元素进小根堆,保证元素进入合理的位置
然后还要根据两个堆元素个数,调整两堆大小,平衡Queue<Integer> heapD = new PriorityQueue<Integer>(((o1, o2) -> o2.compareTo(o1)));//前一半 大顶堆
Queue<Integer> heapX = new PriorityQueue<Integer>();//后一半 小根堆
public void Insert(Integer num) {
heapD.offer(num);//先进大根堆(前一半)
heapX.offer(heapD.poll());//再大根堆顶移到小根堆 平衡一下
while (heapD.size()<heapX.size()) heapD.offer(heapX.poll());//前一半不能少于后一半
}
public Double GetMedian() {
int n = heapD.size()+heapX.size();
if(n%2==1) return heapD.peek()*1.0;
return (heapX.peek()+heapD.peek())/2.0;
}
JZ65 不用加减乘除做加法
否则得动点脑筋了
二进制加法:异或就是本位和 相与就是进位public class JZ65 {
public int Add(int num1,int num2) {
int sum = num1;
int add = num2;
while (add!=0){
sum = num1^num2;//每位异或得本位和
add = (num1&num2)<<1;//每位相与得进位 => 但是进位都是进给高位的 所以整体左移一位
//然后就是本位和与进位再次相加即可(又是加法 同样得套路即可) =》 直到其中一个为0(add==0)就可以结束了 ,没必要再做加法了
num1 = sum;
num2 = add;
}
return sum;
}
public static void main(String[] args) {
JZ65 t = new JZ65();
System.out.println(t.Add(9, 6));
}
}
JZ15 二进制中1的个数
1、一个数与1相与就得到其二进制最低位是0还是1,这个性质可以来判断奇偶 (因为1的二进制是除了最低位1其他位全部是0)
2、每次与1相与得到最低位二进制是0还是1,然后直接算数右移动即可
3、由于算数移位(正数高位会补0) 负数高位会补1,导致没完没了,所以得控制循环次数32次 public int NumberOf1(int n) {
int sum=0;
int T=32;
while ((T--)!=0){
sum += (n&1);
n=(n>>1);//最低位统计过了 直接丢弃
}
return sum;
}
这就可以通过n==0? 来作为终止条件了。小小优化代码 public int NumberOf1(int n) {
int sum=0;
while (n!=0){
sum += (n&1);
n=(n>>>1);//最低位统计过了 直接丢弃
}
return sum;
}
public int NumberOf1(int n) {
int sum=0;
for(int i=0;i<32;i++){
System.out.print(((1<<i)&n)+" ");
if( ((1<<i)&n) !=0 ){//结果是100000 不是每次都1
sum++;
}
}
return sum;
}
JZ16 数值的整数次方
public double Power(double base, int exponent) {
if(exponent<0){
base = 1/base;
exponent*=-1;
}
double ans = 1;
while ((exponent--)!=0) ans*=base;
return ans;
}
public double Power(double x, int n) {
if (n < 0) {
x = 1 / x;
n = -n;
}
double ans = 1;
while (n != 0) {
if (n % 2 == 1) ans *= x; //奇数提出1个幂 就变偶数次幂了 (不用n-- 因为对于奇数 (n/2)==(n-1)/2)
x *= x; //基数平方
n /= 2; //幂就可以减半了
}
return ans;
}
JZ56 数组中只出现一次的两个数字
// 假设结果是 a b
// 全部异或最终得到的就是 a^b
// 那么a^b的哪一位为1,则说明这两个数二进制对应的这两位一定不同,按照这一位是0还是1将数组划分为2组,再分别异或即可
// 因为相同的两个数对应的二进制的每一位都相同,所以一定会被分到同一组import java.util.Arrays;
public class JZ56 {
public int[] FindNumsAppearOnce (int[] array) {
int res = 0;
for (int i : array) res ^= i;
int t=0;
while (((1<<t)&res) == 0) t++;//找到res最低位的那个1
t = 1<<t;
int a=0,b=0;
for (int i : array) {
if((i&t)==0) a^=i;
else b^=i;
}
if(a>b) return new int[]{b,a};
return new int[]{a,b};
}
public static void main(String[] args) {
JZ56 t = new JZ56();
int[] ints = t.FindNumsAppearOnce(new int[]{1,2,3,3,2,9});
System.out.println(Arrays.toString(ints));
}
}
JZ64 求1+2+3+…+n
// 不能用乘除但是没说不能用加减啊
// 立刻想到了递归 return n+Sum_Solution(n-1)
// 但是递归出口咋办?不能用if啊
// 接下来就是考c语言语法了(扣语法?竟然有用)=》巧用短路
public class JZ64 {
public int Sum_Solution(int n) {
//&&短路巧妙实现了if判断 n>0才会执行&&后面的语句
boolean flag = (n > 0) && (n += Sum_Solution(n - 1)) > 0;
return n;
}
public static void main(String[] args) {
JZ64 t = new JZ64();
System.out.println(t.Sum_Solution(100));
}
}
JZ29 顺时针打印矩阵
import java.util.ArrayList;
public class JZ29 {
public ArrayList<Integer> printMatrix(int[][] matrix) {
m = matrix.length;
n = matrix[0].length;
if(m==0||n==0) return this.ans;
visted = new boolean[m][n];
this.matrix= matrix;
int flag = 0;//0右 1下 2左 3上
dfs(0, 0, flag);
return this.ans;
}
int[] dx = {0, 1, 0, -1};
int[] dy = {1, 0, -1, 0};
int m,n;
boolean[][] visted = null;
int[][] matrix = null;
ArrayList<Integer> ans = new ArrayList<>();
boolean judge(int x,int y,int flag){
if(x<0||x>=m||y<0||y>=n||visted[x][y]) return false;
return true;
}
private void dfs(int x, int y, int flag) {
visted[x][y]=true;
//System.out.print(matrix[x][y]+" ");
ans.add(matrix[x][y]);
if (!judge(x+dx[flag],y+dy[flag],flag)) flag = (flag+1)%4;
if(judge(x+dx[flag],y+dy[flag],flag))//再不行直接退出就行了
dfs(x+dx[flag],y+dy[flag],flag);
}
public static void main(String[] args) {
int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
JZ29 t = new JZ29();
ArrayList<Integer> ans = t.printMatrix(matrix);
System.out.println(ans);
}
}
直接写四次循环,每次循环完收缩下边界即可import java.util.ArrayList;
public class JZ29_a {
public ArrayList<Integer> printMatrix(int[][] matrix) {
ArrayList<Integer> ans = new ArrayList<Integer>();
int left = 0, right=matrix[0].length-1;
int up = 0, down = matrix.length-1;
if(right<0||down<0) return ans;
int x=0,y=0;
while (true){
for(y=left;y<=right;y++) ans.add(matrix[x][y]);
up++;y--;
if(up>down) break;
for(x=up;x<=down;x++) ans.add(matrix[x][y]);
right--;x--;
if(right<left) break;
for(y=right;y>=left;y--) ans.add(matrix[x][y]);
down--;y++;
if(down<up) break;
for(x=down;x>=up;x--) ans.add(matrix[x][y]);
left++;x++;
if(left>right) break;
}
return ans;
}
public static void main(String[] args) {
//int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
int[][] matrix = {{1, 2, 3, 4,5}};
JZ29_a t = new JZ29_a();
ArrayList<Integer> ans = t.printMatrix(matrix);
System.out.println(ans);
}
}
JZ61 扑克牌顺子
import java.util.*;
public class Solution {
public boolean IsContinuous(int[] numbers) {
int max = 1, min = 14; //范围就是1~14
int[] Hash = new int[15];
for (int n : numbers) {
if (n == 0) {
Hash[n]++;
continue;
}
if (Hash[n] > 0) return false;
max = Math.max(max, n);
min = Math.min(min, n);
Hash[n]++;
}
//return Hash[0]==4 || max-min==4-Hash[0] || max - min == 4;
// 完全不必上面这么麻烦,无重复,极差小于5,0就可以自动补位
return max-min<5;
}
}
public boolean IsContinuous(int[] numbers) {
Set<Integer> set = new HashSet<Integer>();
for (int n : numbers) {
if(n==0) continue;
if(set.contains(n)) return false;
set.add(n);
}
return Collections.max(set)-Collections.min(set) < 5;
}
JZ67 把字符串转换成整数(atoi)
public class JZ67 {
public int StrToInt (String s) {
//if(s.length()<=0) return 0;
char[] arr = s.toCharArray();
int t=0;
while (t<s.length()&&arr[t]==' ') t++;
if(t>=s.length()) return 0;
int flag = 1;
if(arr[t]=='-') flag=-1;
if(arr[t]=='+'||arr[t]=='-') t++;
long ans=0;
while (t<s.length()&&Character.isDigit(arr[t])){
ans = ans*10 + (arr[t]-'0');
t++;
if(ans*flag>Integer.MAX_VALUE) {
ans = Integer.MAX_VALUE*1l;
break;
}
if(ans*flag<Integer.MIN_VALUE){
ans = Integer.MIN_VALUE*-1l;
break;
}
}
return Integer.parseInt(String.valueOf(ans*flag));
}
public static void main(String[] args) {
JZ67 t = new JZ67();
// System.out.println(t.StrToInt("82"));
// System.out.println(t.StrToInt(" -12 "));
// System.out.println(t.StrToInt("4396 clearlove"));
// System.out.println(t.StrToInt("clearlove 4396"));
//System.out.println(t.StrToInt("-987654321111"));
// System.out.println(t.StrToInt(""));
System.out.println(t.StrToInt(" "));
/*System.out.println(Integer.MIN_VALUE);//-2147483648
System.out.println(Integer.MIN_VALUE*-1);//-2147483648
System.out.println(Integer.MIN_VALUE*-1l);//2147483648*/
}
}
JZ20 表示数值的字符串
public boolean isNumeric (String str) {
try {
Float.parseFloat(str);
return true;
} catch (NumberFormatException e) {
return false;
}
}
还是懒,想用正则又不会,只能暴力public boolean isNumeric (String str) {
String[] pattern = {
"(\\s)*[+-]?(\\d)*\\.(\\d+)[eE][+-]?\\d+(\\s)*",
"(\\s)*[+-]?(\\.)?(\\d+)[eE][+-]?\\d+(\\s)*",
"(\\s)*[+-]?\\.(\\d+)(\\s)*",
"(\\s)*[+-]?(\\d+)(\\.)?(\\s)*",
"(\\s)*[+-]?(\\d+)\\.[eE]?\\d+(\\s)*",
};
for (String p : pattern) {
if (Pattern.matches(p, str)) return true;
}
return false;
}
public boolean isNumeric (String str) {
String[] pattern = {
"[+-]?\\d*\\.?\\d+|[+-]?\\d*\\.?\\d+[eE][+-]?\\d+",
"(\\s)*[+-]?(\\d+)(\\.)?(\\s)*",
"(\\s)*[+-]?(\\d+)\\.[eE]?\\d+(\\s)*",
};
for (String p : pattern) {
if (Pattern.matches(p, str)) return true;
}
return false;
}
JZ66 构建乘积数组
public int[] multiply(int[] A) {
int[] mul = new int[A.length];
Arrays.fill(mul, 1);
for (int i = 0; i < A.length; i++) {
for (int i1 = 0; i1 < mul.length; i1++) {
if (i != i1) mul[i1] *= A[i];
}
}
return mul;
}
public int[] multiply(int[] A) {
int[] B = new int[A.length];
B[0] = 1;
for (int i = 1; i < A.length; i++) {
B[i] = B[i - 1] * A[i-1];//注意是A[i-1]
}
int[] C = new int[A.length];
C[A.length - 1] = 1;
for (int i = A.length - 2; i >= 0; i--) {
C[i] = C[i + 1] * A[i+1];//注意是A[i+1]
}
for (int i = 0; i < B.length; i++) {
B[i] *= C[i];
}
return B;
}
public int[] multiply(int[] A) {
int[] B = new int[A.length];
B[0] = 1;
for (int i = 1; i < A.length; i++) {
B[i] = B[i - 1] * A[i-1];//注意是A[i-1]
}
int temp = 1;
for (int i = A.length - 1; i >= 0; i--) {
B[i] *= temp;
temp*=A[i];
}
return B;
}
JZ50 第一个只出现一次的字符
public int FirstNotRepeatingChar(String str) {
char[] chars = str.toCharArray();
int[] Hash = new int[128];//ASCII只有128个
for (int i = 0; i < chars.length; i++)
Hash[chars[i]]++;
//遍历原字符串 才能保证找到的是第一个出现一次的
for (int i = 0; i < chars.length; i++) {
if(Hash[chars[i]]==1) return i;
}
return -1;
}
JZ5 替换空格
public String replaceSpace (String s) {
return s.replace(" ","%20");
}
public String replaceSpace (String s) {
char[] chars = s.toCharArray();
String ans="";
String temp="";
for (int i = 0; i < chars.length; i++) {
if(chars[i]==' '){
ans += temp + "%20";
temp = "";
}else {
temp += String.valueOf(chars[i]);
}
}
return ans+temp;
}
public String replaceSpace (String s) {
char[] ans = new char[s.length()*3];//极端情况全是空格 长度膨胀3倍
int index = 0;
char[] chars = s.toCharArray();
for (char c : chars) {
if(c==' '){
ans[index++]='%';
ans[index++]='2';
ans[index++]='0';
}else {
ans[index++]=c;
}
}
return new String(ans,0,index);
}
JZ21 调整数组顺序使奇数位于偶数前面(一)
public int[] reOrderArray(int[] array) {
int[] odd = new int[array.length];
int[] even = new int[array.length];
int n1 = 0, n2 = 0;
for (int a : array) {
if (a % 2 == 1) odd[n1++] = a;
else even[n2++] = a;
}
//even放到odd后面
for (int i = 0; i < n2; i++) odd[n1++] = even[i];
return odd;
}
// 空间O(1) 时间O(n^2)
public int[] reOrderArray(int[] array) {
//遍历 遇到偶数就把他交换到最后面
int finished = 0;
for (int i = 0; i < array.length-finished; i++) {
if(array[i]%2==0){
int t = array[i];
for(int j=i;j<array.length-1;j++) array[j]=array[j+1];
array[array.length-1]=t;
finished++;
i--;
}
}
return array;
}
JZ39 数组中出现次数超过一半的数字
但是嘛,408真题,丝毫不惧了
遇到自己t++
非自己 t–
t =0时换base为当前
过半的必然最终成为basepublic int MoreThanHalfNum_Solution(int[] array) {
int t = 1;
int base = array[0];
for (int i = 1; i < array.length; i++) {
if (base != array[i]) {
t--;
if (t == 0) {
base = array[i];
t = 1;
}
}else t++;
}
// 真要超过一半,一定会被筛选出来. 保证有解 直接返回即可
return base;
}
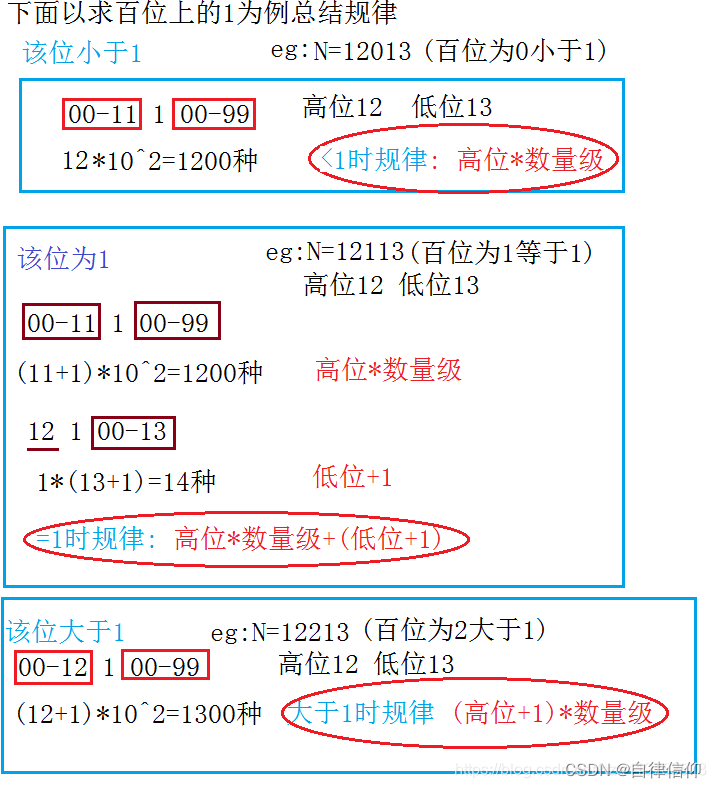
JZ43 整数中1出现的次数(从1到n整数中1出现的次数)
public int NumberOf1Between1AndN_Solution(int n) {
int num = 0;
for(int i=1;i<=n;i++){
int x = i;
while (x!=0){
if(x%10==1) num++;
x/=10;
}
}
return num;
}
public int NumberOf1Between1AndN_Solution(int n) {
//找规律
char[] chars = String.valueOf(n).toCharArray();
int l = chars.length-1;
int num =0;
for(int i=l;i>=0;i--){
int t = chars[i]-'0';
int GW = i>0?Integer.parseInt(new String(chars,0,i)):0;//高位
int SL = (int) Math.pow(10,l-i);//数量级
int DW = (l-i>0)?Integer.parseInt(new String(chars,i+1,l-i)):0;//低位
if(t<1) num += GW*SL;//高位*数量级
else if(t==1) num += (GW*SL+DW+1);//高位*数量级+低位+1
else num += (GW+1)*SL;//(高位+1)*数量级
}
return num;
}
public int NumberOf1Between1AndN_Solution(int n) {
int num =0,k=0;
while (true){
int self = (int) ((n/Math.pow(10,k))%10);
int low = k>0? (int) (n % Math.pow(10, k)) :0;
int high = (int) (n/Math.pow(10,k+1));
if(self<1) num += high*Math.pow(10,k);
else if(self==1) num += high*Math.pow(10,k) + (low+1);
else num += (high+1)*Math.pow(10,k);
k++;
if(high<1) break;//第一次high=0是在处理最高位,实属正常
}
return num;
}
JZ45 把数组排成最小的数
import java.util.Arrays;
import java.util.Comparator;
public class JZ45 {
public String PrintMinNumber(int [] numbers) {
if(numbers.length<1) return "";
String[] strs = new String[numbers.length];
for (int i = 0; i < numbers.length; i++) strs[i] = numbers[i]+"";
Arrays.sort(strs,new MyComparator());
//System.out.println(Arrays.toString(strs));
String ans="";
for (String str : strs) ans += str;
return ans;//不需要去掉前导0
}
public static void main(String[] args) {
JZ45 t = new JZ45();
//String s = t.PrintMinNumber(new int[]{3, 32, 321});
String s = t.PrintMinNumber(new int[]{});
System.out.println(s);
}
}
class MyComparator implements Comparator<String> {
@Override
public int compare(String o1, String o2) {
return (o1+o2).compareTo(o2+o1);
}
}
import java.util.*;
public String PrintMinNumber(int [] numbers) {
if (numbers.length < 1) return "";
String[] strs = new String[numbers.length];
for (int i = 0; i < numbers.length; i++) strs[i] = numbers[i] + "";
Arrays.sort(strs, new Comparator<String>() {
@Override
public int compare(String o1, String o2) {
return (o1 + o2).compareTo(o2 + o1);
}
});
String ans = "";
for (String str : strs) ans += str;
return ans;//不需要去掉前导0
}
JZ49 丑数
// 结合小顶堆,弹出index次即可 多好呀,每次加3个最小的就行了
// 都是动态扩张 多好 别想多了import java.util.HashMap;
import java.util.PriorityQueue;
public int GetUglyNumber_Solution(int index) {
if(index==0) return 0;
PriorityQueue<Long> heep = new PriorityQueue<>();
HashMap<Long, Integer> map = new HashMap<>();
int fac[]={2,3,5};
heep.offer(1l);
long top=1;
while (index>0){
top = heep.poll();
//System.out.println(top);
index--;
for (int i : fac) {
if(map.get(i*top)==null){
map.put(i*top,1);
heep.offer(i*top);
}
}
}
return (int) top;
}
JZ74 和为S的连续正数序列
ArrayList<Integer> seqList(int m,int n){
ArrayList<Integer> list = new ArrayList<>();
for(int i=m;i<=n;i++) list.add(i);
return list;
}
public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
ArrayList<ArrayList<Integer>> ans = new ArrayList<ArrayList<Integer>>();
for(int i=1;i<sum-1;i++){
for(int j=i+1;j<sum;j++){
if((i+j)*(j-i+1)/2==sum) ans.add(seqList(i,j));
if((i+j)*(j-i+1)/2>sum) break;//适当剪枝
}
}
return ans;
}
ArrayList<Integer> seqList(int m,int n){
ArrayList<Integer> list = new ArrayList<>();
for(int i=m;i<=n;i++) list.add(i);
return list;
}
public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
ArrayList<ArrayList<Integer>> ans = new ArrayList<ArrayList<Integer>>();
int l=1,r=2;
while (l<r){
int t = (l+r)*(r-l+1)/2;
if(t==sum) {
ans.add(seqList(l,r));
r++;l++;//别忘了这时候指针也要动
}
else if(t<sum) r++;
else l++;
}
return ans;
}
JZ57 和为S的两个数字
public ArrayList<Integer> FindNumbersWithSum(int [] array, int sum) {
ArrayList<Integer> ans=new ArrayList<>();
int i=0,j=array.length-1;
while (i<j){
int t = array[i]+array[j];
if(t==sum) {
ans.add(array[i]);ans.add(array[j]);
break;
}else if(t<sum) i++;
else j--;
}
return ans;
}
public ArrayList<Integer> FindNumbersWithSum(int [] array, int sum) {
ArrayList<Integer> ans=new ArrayList<>();
HashMap<Integer, Integer> map = new HashMap<>();
for (int i : array) {
if(map.get(i)==null) map.put(i,1);
else map.put(i,map.get(i)+1);
}
for (int i : array) {
if(map.get(i)!=null){
map.put(i,map.get(i)-1);
if(map.get(sum-i)!=null&&map.get(sum-i)>0){
ans.add(i);ans.add(sum-i);
break;
}
}
}
return ans;
}
JZ58 左旋转字符串
public String LeftRotateString(String str,int n) {
if(str==null||str.trim().length()==0) return "";
n = n%str.length();
StringBuilder ans = new StringBuilder();
ans.append(new StringBuilder(str.substring(0,n)).reverse());//前n逆置
ans.append(new StringBuffer(str.substring(n,str.length())).reverse());//后l-n逆置
return ans.reverse().toString();//再整体逆置
}
JZ62 孩子们的游戏(圆圈中最后剩下的数)
public int LastRemaining_Solution(int n, int m) {
ArrayList<Integer> ans = new ArrayList<>();
for(int i=0;i<n;i++) ans.add(i);
int start=0;
while (ans.size()>1){
start = (start+m-1)%ans.size();
ans.remove(start);
}
return ans.get(0);
}
直接从题解里拿过来的,写得不错如果只求最后一个报数胜利者的话,我们可以用数学归纳法解决该问题,为了讨 论方便,先把问题稍微改
变一下,并不影响原意:
问题描述:n个人(编号0~(n-1)),从0开始报数,报到(m-1)的退出,剩下的人 继续从0开始报数。求胜利者
的编号。
我们知道第一个人(编号一定是m%n-1) 出列之后,剩下的n-1个人组成了一个新 的约瑟夫环(以编号为
k=m%n的人开始):
k k+1 k+2 ... n-2, n-1, 0, 1, 2, ... k-2并且从k开始报0。
现在我们把他们的编号做一下转换:
k --> 0
k+1 --> 1
k+2 --> 2
...
...
k-2 --> n-2
k-1 --> n-1
变换后就完完全全成为了(n-1)个人报数的子问题,假如我们知道这个子问题的解: 例如x是最终的胜利者,那
么根据上面这个表把这个x变回去不刚好就是n个人情 况的解吗?!!变回去的公式很简单,相信大家都可以推
出来:x'=(x+k)%n。
【解释:】
上面有两列数,第1列是真实的序号,第二列是第二次报数的序号,但是第二列可以看成一开始只有n-1个人的从
头开始的报数问题
假设这个报数问题的最终解是x,对应上次的序号不就是x+k吗? 当然后面可能溢出 就模一下n=》 (x+k)%n
【模n进一步解释:】 (n-2+k)%n=k-2 (n-1+k)%n=k-1 不是正好对应上了吗?
令f[i]表示i个人玩游戏报m退出最后胜利者的编号,最后的结果自然是f[n]。
递推公式
f[1]=0;
f[i]=(f[i-1]+m)%i; (i>1)
有了这个公式,我们要做的就是从1-n顺序算出f[i]的数值,最后结果是f[n]。 因为实际生活中编号总是从1开始,我们输出f[n]+1。
public int LastRemaining_Solution(int n, int m) {
if(n==1) return 0;
int x = LastRemaining_Solution(n-1,m);
int k = m%n;
return (x+m)%n;
}
public int LastRemaining_Solution(int n, int m) {
if (n < 1 || m < 1)
return -1;
int last = 0;//假设一开始只有n=1 那么last必然等于0
for (int i = 2; i <= n; i++){
last = (last + m) % i;//不断往上回推
System.out.println(last);//中间结果不对 最后结果对的
}
return last;
}
JZ75 字符流中第一个不重复的字符
char[] caseout = new char[1000];
int n = 0;
public void Insert(char ch) {
caseout[n++]=ch;
Hash[caseout[n-1]]++;
}
int[] Hash = new int[128];
public char FirstAppearingOnce() {
for (int i = 0; i < n; i++) {
if(Hash[caseout[i]]==1) return (char) caseout[i];
}
return '#';
}
LinkedList<Character> q = new LinkedList<>();
int[] Hash = new int[128];
public void Insert(char ch) {
q.offer(ch);
Hash[ch]++;
}
public char FirstAppearingOnce() {
while (!q.isEmpty()){
Character top = q.peek();
if(Hash[top]==1) return top; // 要么下面弹出 要么这里返回
else q.poll();//不止1 直接弹出 (下次查询就快了)
}
return '#';
}
JZ14 剪绳子
public int cutRope(int target) {
int[] dp = new int[61];
if(target<4) return target-1;
// 不分最大 (并不是对应的返回值 没办法必须这么办 不然没法状态转移)
dp[2] = 2;
dp[3] = 3;
dp[4] = 4;
for(int i=5;i<=target;i++){
for(int j=2;j<i;j++){
dp[i] = Math.max(dp[i],j*dp[i-j]);
}
}
return dp[target];
}

细节: 数学推导出,整数的话只有按照3来进行等分才是最大的,但是最后剩个1也就是最后长度4应该分成2*2。(其他呢?会不会也有其他情况?不知道诶,应该没有吧,毕竟确实3等分、e等分最大)public int cutRope(int target) {
int n = target/3;
if(target%3==1) return (int) (Math.pow(3,n-1)*4);
if(target%3==2) return (int) (Math.pow(3,n)*2);
return (int) Math.pow(3,n);
}
JZ81 调整数组顺序使奇数位于偶数前面(二)
空间复杂度 O(1)
稍作思考,就想到了快排的思想,比较规则是奇数在偶数前面,一趟遍历即可public int[] reOrderArrayTwo (int[] array) {
// 首尾双向指针 交换元素
int l=0,r=array.length-1;
while (l<r){
while (l<r&&array[l]%2!=0) l++; // 前边找第一个偶数 注意lJZ83 剪绳子(进阶版)
public long cutRope(long number) {
//约瑟夫环,尽可能多地分出3,最后若有一个4得分成2*2
long n = number / 3;
long r = number % 3;
if (r == 0) return ((long) Math.pow(3l, n)) % 998244353l;
if (r == 1) return (long) (Math.pow(3l, n - 1) * 4l) % 998244353l;
return ((long) (Math.pow(3l, n) * 2l)) % 998244353l;
}
public long cutRope(long number) {
if (number < 4) return number - 1;
//约瑟夫环,尽可能多地分出3,最后若有一个4得分成2*2
long mod = 998244353;
long n = number / 3;
long r = number % 3;
long ans = 1;
long exp = 3;
//快速幂
while (n >= 1) {
if (n % 2 == 1) ans = (ans * exp) % mod;
exp = (exp * exp) % mod;//细节 幂也要 %mod (小细节卡了好久)
n /= 2;
}
if (r == 1) ans = (ans / 3 * 4) % mod;
if (r == 2) ans = (ans * 2) % mod;
return ans % mod;
}
插入一点数论的知识

JZ17 打印从1到最大的n位数
public int[] printNumbers (int n) {
n = (int) Math.pow(10,n)-1;
int[] a = new int[n];
for (int i = 1; i <= n; i++) {
a[i-1]=i;
}
return a;
}