一篇玩转RBF径向基神经网络入门+实例代码

本站原创文章，转载请说明来自《老饼讲解-BP神经网络》bp.bbbdata.com

RBF径向基神经网络由Powell在1985年提出，广泛应用于数值预测
本文深入浅出地介绍径向基神经网络是什么，并展示matlab实现径向基神经网络的例子
帮助初学者直接了当地理解径向基神经网络的思想与应用

---

目录

一、RBF神经网络是什么

1.1 RBF神经网络是什么

二、 关于径向基函数的数学表达式   

2.1 径向基神经网络的通用数学表达式

2.2 径向基神经网络的具体数学表达式   

三、径向基神经网络的求解    

3.1 径向基神经网络的求解方法

3.2 精确求解和OLS求解的区别    

四、RBF神经网络代码实例

4.1 RBF神经网络实例与matlab代码实现 

4.2 运行结果解释

---

一、RBF神经网络是什么

本节快速、简单、直接介绍RBF神经网络是什么

1.1 RBF神经网络是什么

---

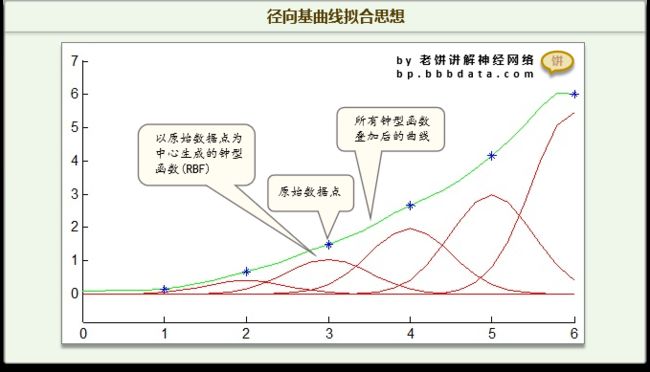
RBF神经网络简单的说，

就是用多个钟型函数(径向基)来凑合出目标曲线 

从图中可以看到，
RBF神经网络以6个原始数据点（图中蓝色的点）为中心，生成了6个RFB曲线
6个RBF曲线叠加后就是一条能够光滑地拟合原始数据点的曲线（绿色）
 径向基神经网络主要就是利用了RFB函数只对中心邻近区域有影响的特性(局部性)
从而在每个局部都用一个径向基去凑合，最终达到全局拟合
因此，可易知
RBF神经网络模型的数学表达式类似如下形式

---

二、 关于径向基函数的数学表达式   

本节介绍径向基神经网络的数学表达式和网络拓扑图

2.1 径向基神经网络的通用数学表达式

---

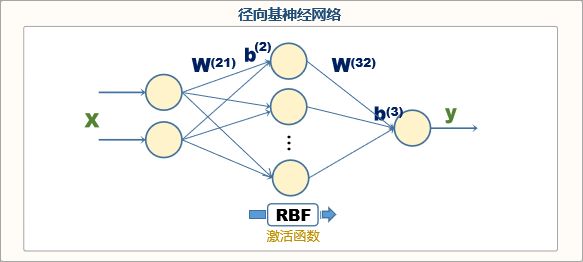
一个2输入、3个RBF神经网络的数学表达式如下：

其中
RBF内的b和W用于调节径向基的宽度和x轴位置
RBF外的W和b用于调节径向基的高度和y轴位置
往往也会用网络拓扑图来表示，如下

  
径向基神经网络的训练就是求解上述表达式中各个RBF的w和b，
使得最终网络的输出与真实y值一致 

2.2 径向基神经网络的具体数学表达式   

---

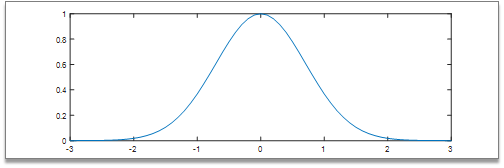
我们使用的径向基函数(Radial Basis Function)一般都是高斯函数

它的图象如下

由于
所以具体使用时，
径向基神经网络的表达式如下：

其中
dist 代表欧氏距离函数
例如 

---

三、径向基神经网络的求解    

本节介绍径向基神经网络的求解方法

3.1 径向基神经网络的求解方法

---

径向基神经网络的常见基本求解方法有三种
1. 精确求解            
2. OLS求解法         
3. K-means聚类法
在matlab的工具箱中，
newrbe 就是使用精确求解方法
newrb 则是使用OLS求解法      
matlab没有实现k-means求解径向基神经网络的方法

3.2 精确求解和OLS求解的区别    

---

关于RBF神经网络的精确求解
精确求解以每个样本为中心，n个样本就生成n个径向基
然后预设径向基的宽度，最后再求解径向基的高度和阈值
它的最大特色是，训练数据的输出误差为0，因此称为精确求解

关于RBF神经网络的OLS求解

OLS求解法与精解求解的主要思想差不多，
只不过精确求解有n个样本就有n个径向基，网络会非常庞大和复杂
因此，OLS是将径向基逐个添加进来，如下

 
可以看到，随着径向基的添加，网络误差在下降，
从而我们可以选择误差较小，而又能满足我们需求径向基个数作为我们最终的网络

四、RBF神经网络代码实例

本节展示一个RBF神经网络的实例，从中更具体的学习和掌握RBF神经网络

4.1 RBF神经网络实例与matlab代码实现 

---

下面演示使用matlab的newrb函数，
实现一个径向基神经网络拟合以下数据点

 代码实现如下

%代码说明：径向基newrb的matlab工具箱使用Demo
%来自《老饼讲解神经网络》bp.bbbdata.com ,matlab版本：2018a
%-----------------------------------------------------
%----数据准备----
close all 
x  = [-2 -1 0 1 2];
y  = [3 2 3 1 2];  % 输出数据
%----网络训练----
[net,tr] = newrb(x, y, 0.01, 0.5);    % 以X，Y建立径向基网络，目标误差为0.01，径向基的宽度参数spread=0.5
simY = sim(net,x)                  % 用建好的网络拟合原始数据
perf = tr.perf
w21 = net.iw{1}
b2  = net.b{1}
w32 = net.lw{2,1}
b3  = net.b{2}
%----绘制拟合曲线----
figure(1);
hold on 
t   = -2:0.1:2;              
rbf = repmat(w32',1,size(t,2)).* exp(-(repmat(b2,1,size(t,2)).*dist(w21,t)).^2);
simt = sum(rbf) + b3;
for i = 1:size(rbf,1)
    plot(t,rbf(i,:),':')
end
plot(x,y,'*')  
plot(t,simt,'r')  

4.2 运行结果解释

---

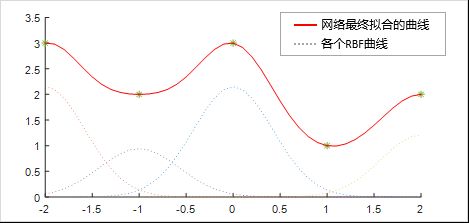
上述代码运行后输出如下

  

 
  由于程序中我们设置了误差目标为0.01，
当添加了4个RBF的时候，误差就已经满足要求
可以看到，网络拟合的数据与原数据基本一致 
下面是最终训练好的径向基神经网络的权重和阈值

将权重、阈值代入径向基神经网络的数学表达式，
即可得到最终的模型表达式为：

---

相关文章

---

老饼讲解|【原理】径向基神经网络是什么

老饼讲解|【结构】径向基神经网络的拓扑与数学表述

老饼讲解|【原理】径向基神经网络-精确求解原理详述