基础算法-双指针,滑动窗口,位运算,区间离散化

双指针

两种类型

 

 

for(int i=0,j=0;i

双指针最核心的性质 可以优化

输入一个字符串 把每个单词输出出来

i找到单词开头

j找到空格

vector rs;
for(int i=0,j=0;i

最长不重复子串

滑动窗口

i,j指针最多走2n步

int left = 0, right = 0;

while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    right++;
    
    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
		默认在这里 r 会落在 第一个不符合的位置
		         l 会落在 区间的第一个数
}

 

#include
#include
#include
#include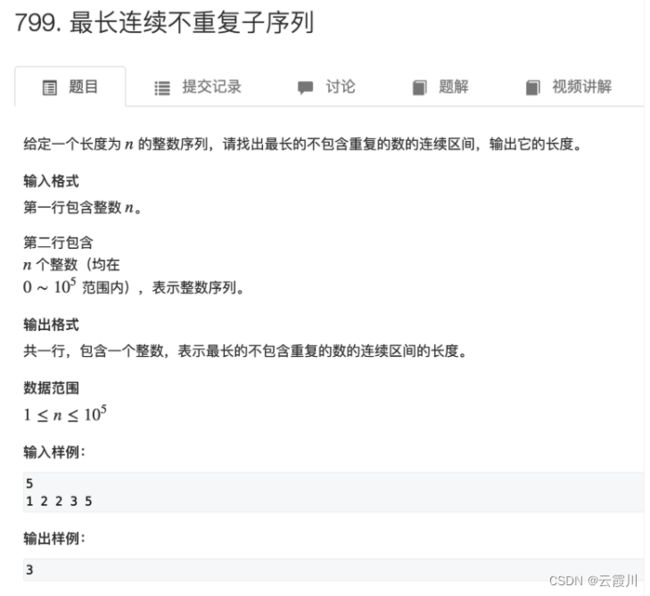

最小覆盖子串

 

#include
#include
#include

位运算

最常用的两个操作

n的二进制 表示中 第k位数是几 从0开始

 

先把第k位移到最后一位

n>>k

然后与1

&1

结合起来

n>>k&1

lowbit(x) 返回x的最后一位1后面的数 比如10100 返回100

负数即为补码 即为取反+1

4 

就可以通过lowbit 求出 一个数中的1的个数

 

不断求它的lowbit即可

#include
#include
using namespace std;

// 1001000  求的 1000
int lowbit(int x)
{
    return x&-x;
}
// 1001000 从0位开始 求k位的数
int k_bit(int x,int k)
{
    return x>>k&1;
}
int main()
{
    int n=0;
    cin>>n;
    for(int i=0;i>m;
        int ans=0;
        while(m)
        {
            m-=lowbit(m);
            ans+=1;
        }
        cout<

离散化

比如一个区间 它的大小在

 

但我们仅用到了其中的n个数,因此我们可以将它的区间进行映射

如。0 100 300 300000 4000000 500000000

可以映射成

0 1 2 3 4 5

具体代码如下 使用二分搜索

比如 alls中是我们所有赋值与查询用到的数 有
100 0 300 300 300000 40000000 50000000
我们首先排序alls
sort(alls.begin(),alls.end());
并去除重复值
alls.erase(unique(alls.begin(),alls.end()),alls.end());
然后 查询某个 区间[l1,l2]
就可以将l1,l2 映射成 k1,k2
int k1= lower_bound(alls.begin(),alls.end(),l1)-alls.begin();
int k2= lower_bound(alls.begin(),alls.end(),l2)-alls.begin();

 

需要提前知道要有哪些值 查询和用到

如以下这道题

 

 

#include
#include
#include
#include