三相三线制逆变器的dq解耦控制

1. 三相三线制逆变器拓扑

  三相三线制逆变器的拓扑如下图所示，其中开关变换器的端口线电压是$U_{AB}$，$U_{BC}$和$U_{CA}$，负载线电压是$v_{ab}$，$v_{bc}$和$v_{ca}$，滤波电容为三角形连接，如果变成星型连接，则容值变成3C。假设负载是星型连接，且三相负载的连接点是O点，则可认为三相星型连接电容和三相星型连接负载处于并联状态，便于后面的简化与建模，假定O点是参考电位点，则$U_A$和$v_a$分别是A相的端口相电压和负载相电压，而且后面的dq变换都是针对相电压进行的。

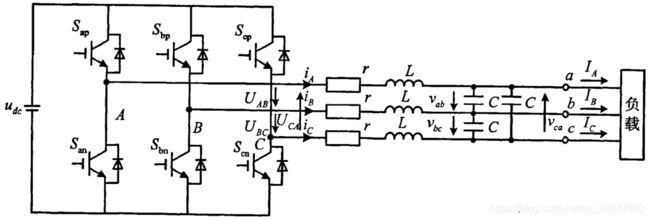
2. 建模

2.1 三相dq变换

  三相dq变换和单相dq变换类似，都是包含很多种形式，主要是在$sin\theta$，$cos\theta$，$-sin\theta$，$-cos\theta$之间进行切换，其中进行dq变换以及dq求导变换时，应该将$\theta$看做$wt$。MATLAB中常用的两种dq变换矩阵分别是
$$T_{abc-dq}=\frac{2}{3}\left[\begin{array}{ccc}coswt& cos(wt-\frac{2\pi }{3})& cos(wt+\frac{2\pi }{3})\\ -sinwt& -sin(wt-\frac{2\pi }{3})& -sin(wt+\frac{2\pi }{3})\end{array}\right]$$

$$T_{abc-dq}=\frac{2}{3}\left[\begin{array}{ccc}sinwt& sin(wt-\frac{2\pi }{3})& sin(wt+\frac{2\pi }{3})\\ coswt& cos(wt-\frac{2\pi }{3})& cos(wt+\frac{2\pi }{3})\end{array}\right]$$
  这两个矩阵均满足$$T_{abc-dq}\frac{d_{iabc}}{d_t}=\left[\begin{array}{c}\frac{d_{id}}{d_t}\\ \frac{d_{iq}}{d_t}\end{array}\right]-w\left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]$$

  所以最终dq解耦控制的表达式是一致的。

2.2三相逆变器数学模型

2.2.1 电压模型

  三相逆变器的时域模型如下：
$$\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right]=\left[\begin{array}{c}{U}_A\\ U_B\\ U_C\end{array}\right]-\left[\begin{array}{c}r\ast i_A\\ r\ast i_B\\ r\ast i_C\end{array}\right]-L\left[\begin{array}{c}\frac{d_{iA}}{d_t}\\ \frac{d_{iB}}{d_t}\\ \frac{d_{iC}}{d_t}\end{array}\right]$$
  将其进行dq变换，可得：
$$T_{abc-dq}\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right]=T_{abc-dq}\left[\begin{array}{c}{U}_A\\ U_B\\ U_C\end{array}\right]-T_{abc-dq}\left[\begin{array}{c}r\ast i_A\\ r\ast i_B\\ r\ast i_C\end{array}\right]-T_{abc-dq}L\left[\begin{array}{c}\frac{d_{iA}}{d_t}\\ \frac{d_{iB}}{d_t}\\ \frac{d_{iC}}{d_t}\end{array}\right]$$
  上式中一共四项，其中前三相就是简单的dq变换，但是最后一项的dq变换涉及到导数的dq变换，需要进行处理。
$$T_{abc-dq}\left[\begin{array}{c}{i}_A\\ i_B\\ i_C\end{array}\right]=\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]$$

$$\left[\begin{array}{c}\frac{d_{id}}{d_t}\\ \frac{d_{iq}}{d_t}\end{array}\right]=\frac{d_{T_{abc-dq}{i}_{abc}}}{d_t}=T_{abc-dq}\frac{d_{iABC}}{d_t}+i_{ABC}\frac{d_{T_{abc-dq}}}{d_t}$$

$$T_{abc-dq}\frac{d_{iABC}}{d_t}=T_{abc-dq}\left[\begin{array}{c}\frac{d_{iA}}{d_t}\\ \frac{d_{iB}}{d_t}\\ \frac{d_{iC}}{d_t}\end{array}\right]$$

$$T_{abc-dq}\frac{d_{iABC}}{d_t}=\left[\begin{array}{c}\frac{d_{id}}{d_t}\\ \frac{d_{iq}}{d_t}\end{array}\right]-w\left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]$$
  经过上面的计算，可以得出：
$$\left[\begin{array}{c}{v}_d\\ v_q\end{array}\right]=\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]-r\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]-L\left[\begin{array}{c}\frac{d_{id}}{d_t}\\ \frac{d_{iq}}{d_t}\end{array}\right]+\omega L\left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]$$
  且可以证明，两种dq变换均满足这个表达式。可以发现，这个表达式和之前推导的三相整流器的dq解耦表达式不一致，这是由于电感电流的正方向和之前推导的相反，此处是变换器流向电网。

2.2.2 电流模型

  将三角形连接的电容转换成星型连接后，容值变成3C。根据KCL方程可以列出：
$$3C\left[\begin{array}{c}\frac{d_{va}}{d_t}\\ \frac{d_{vb}}{d_t}\\ \frac{d_{vc}}{d_t}\end{array}\right]=\left[\begin{array}{c}{i}_A\\ i_B\\ i_C\end{array}\right]-\left[\begin{array}{c}{I}_A\\ I_B\\ I_C\end{array}\right]$$

  经过dq变换之后，可得：
$$C\left[\begin{array}{c}\frac{d_{vd}}{d_t}\\ \frac{d_{vq}}{d_t}\end{array}\right]=\omega C\left[\begin{array}{c}{v}_q\\ -v_d\end{array}\right]+\frac{1}{3}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]-\frac{1}{3}\left[\begin{array}{c}{I}_d\\ I_q\end{array}\right]$$

3. dq解耦控制

  建立完数学模型之后，若采用PI控制，则只需要将dq变换后的表达式中的求导项替换成PI表达式即可。值得注意的是，由于滤波电容是三角形连接，所以电压环中耦合项用的是3C, 但是如果换成星型连接，则耦合项中用的是C。也就是说三角形连接的电容C，等效成星型连接的3C，而我们分析控制系统时是根据星型连接来做的。

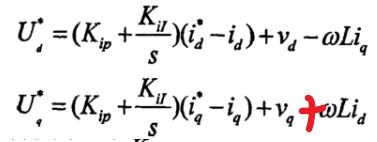
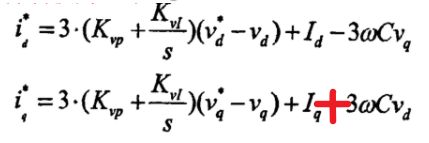
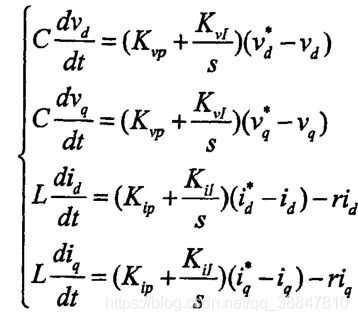
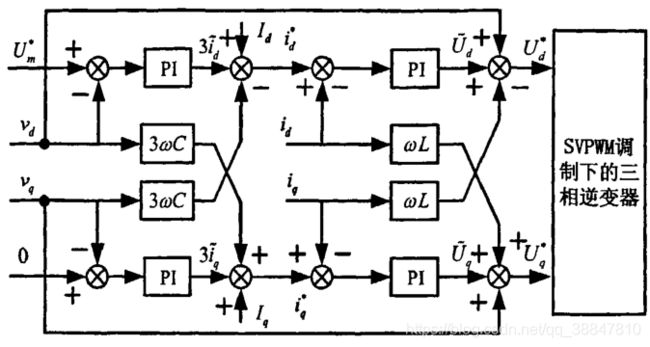  综上所述，逆变器负载电压的电压环输出为电感电流的目标值，而电感电流的电流环输出是端口电压的目标值，将端口电压进行调制，就会得到开关信号。其实体现的就是预测控制的思想。

参考资料

三相逆变器输出电压不平衡的控制研究

反馈与建议

• 邮箱：[email protected]