《MixHop Higher-Order Graph Convolutional Architectures via Sparsified Neighborhood Mixing》阅读笔记

一.论文概述

之前的GCN及其后续工作在图卷积过程中，仅聚合自己的1-hop邻居的消息。作者指出可以将聚合扩大到不同距离的邻居，并基于该idea提出了MixHop，该模型能在不增加额外内存和计算复杂性的同时，生产更加表达能力的节点表示。实验结果表明作者设计的MixHop是有效的。

二.MixHop架构

Two-hop Delta Operator：给定任意邻接矩阵$A$，特征$X$和激活函数$\sigma$，如果存在参数设置和单射$f$，使得网络的输出为：
$$f(\sigma (AX)-\sigma (A^{2}X))$$
则称一个模型能表示two-hop Delta Operator。学习这样的算子允许模型表示邻居之间的特征差异。

以在线社交网络为例，Delta Operators允许模型表示生活在社交圈边缘的用户。为有一个受欢迎的德国朋友的美国人学习一个近似的特征，他可能有大多数直接的朋友讲英语，但有许多朋友的朋友讲德语。这个人可以通过学习卷积滤波器，对比一跳和两跳邻居的英语和德语来表示。

MixHop图卷积层：与经典的GCN不同，作者提出的卷积层的传播规则如下所示：
$$H^{(i+1)}={\Vert }_{j\in P}\sigma (A^j{H}^{(i)}{W}_j^{(i)})$$
其中$P$是整数邻接幂的集合，即$A^j$表示$A$的$j$次幂（$A^0$表示单位阵），$||$表示按列拼接。GCN和MixHop卷积层的对比可视化如下：

在实际过程中作者设置$P=\{0,1,2\}$。注意，在实际计算的时候$A^j{H}^{(i)}$是通过$A(A(A{H}^{(i)})$的方式来计算的。

表达能力：由于每一层在不同列输出不同邻接幂的乘法，下一层的权重能学习列的任意线性组合。通过将正系数分配个某个$A$产生的列，并将负系数分配给另一个列，模型可以学习Delta Operator。相比之下，普通GCN无法表示此类操作，即使堆叠在多层上。

输出层：由于MixHop唯一地混合了来自不同信息集的特征，作者推断约束输出层可能会为不同的任务带来更好的结果。具体做法是，对输出的$s_l$列按$c$个连续列为一组进行划分，然后计算：
$${\tilde{Y}}_O=\sum _{k=1}^{s_l/c}{q}_k{H}_{\ast ,(i{d}_l/c:(i+1)s_l/c)}^{(l)}$$
其中$q_k\in [0,1]$定义了一个有效（valid）分布（softmax的输出），$c$表示类别数。然后计算$Y_O=\mathrm{softmax}({\tilde{Y}}_O)$。这种做法会强迫模型对特征施加更多的权重来选择想要优先考虑的特性。

理论上直观感觉有点牵强。

学习邻接矩阵幂的架构：从MixHop的传播规则可以看出，在每层都包含$P$个权重矩阵$W$，作者认为不同大小的邻接矩阵可能更适合不同的任务和数据集。作者提出Lasso Regularization来自动的学习权重矩阵的大小（指列数）。

三.实验

作者设计了三个实验：

• 合成实验：在合成图中改变边的相关性（同配率homophily），并观测不同的图卷积方法如何响应。
• 现实世界数据集上的实验：作者在现实世界数据集上对比了MixHop和其它Baselines。
• 模型可视化实验：展示一个适当正则化的MixHop模型如何学习不同的、任务相关的体系结构。

同配性指相同标签的节点间的边占所有边的比率。

作者构建了一个2层的MixHop模型，然后在一系列数据集上进行了实验。

实验一：在合成数据集上的实验，作者对比了MixHop和GAT、Chebyshev，2层MLP、Vanilla GCN在不同同配率下，平均准确率的变化情况。

结论：可以看到，随着同配率的升高，其它GNNs也能取得不错的性能，但当同配率较低时，MixHop比其它Baselines要好得多。

实验二：测量了通过模型学得的Delta Operators的数量。

结论：随着同配率增加，识别不同距离的邻居之间有意义的特征差异的需求显著降低。

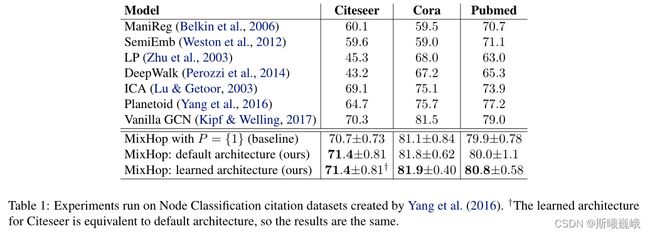
实验三：对比了不同模型在3个现实世界数据集Citeseer、Cora和Pubmed上的结果。

结论：具有邻域混合的高阶图卷积方法可以在真实数据集上优于现有方法。

实验四：验证作者提出的学习权重矩阵架构的有效性。

结论：从结果可以看出在不同数据集上，最终的架构都不同，这表明了不同的架构对于不同的图形数据集是最优的。