移动机器人路径跟踪的设计和仿真模型预测控制（Matlab代码实现）

       目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

在轨迹跟踪应用领域，通常 MPC 建模可根据机器人的控制方式选择基于运动学运动状态方程建模或者基于动力学运动状态方程建模。前者是根据车辆转向的几何学角度关系和速度位置关系来建立描述车辆的运动的预测模型，一般只适用于低速运动场景；后者是对被控对象进行综合受力分析，从受力平衡的角度建模，一般应用在高速运动场景，如汽车无人驾驶。本文基于双轮差速运动学模型，推导实现差速运动的MPC轨迹跟踪控制。 双轮差速运动学线性 MPC 轨迹跟踪实现的基本思路是状态方程–线性化–离散化–预测方程–约束线性化–非线性目标函数转为二次规划–求解最优问题。其中线性化可采用泰勒级数展开忽略高次项的方式，离散化可采用后向差分法，这两个部分都有一定的模型精度丢失。

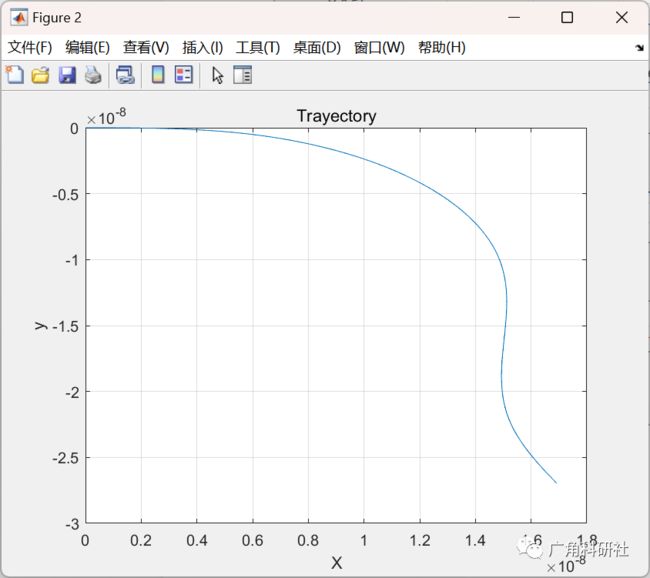
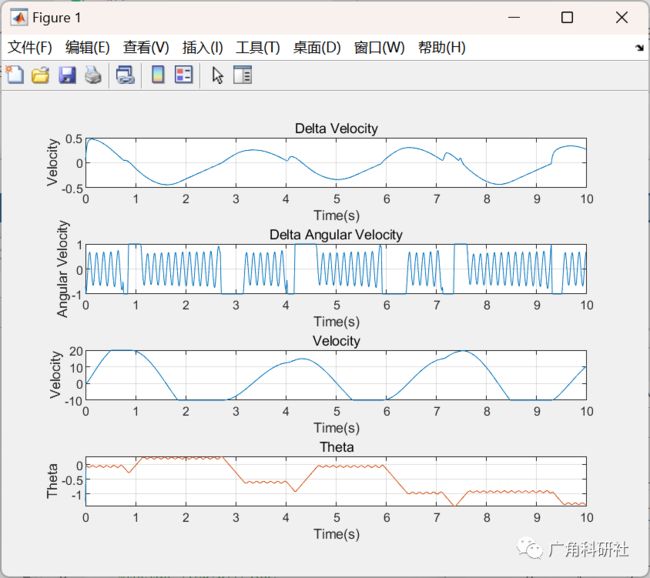
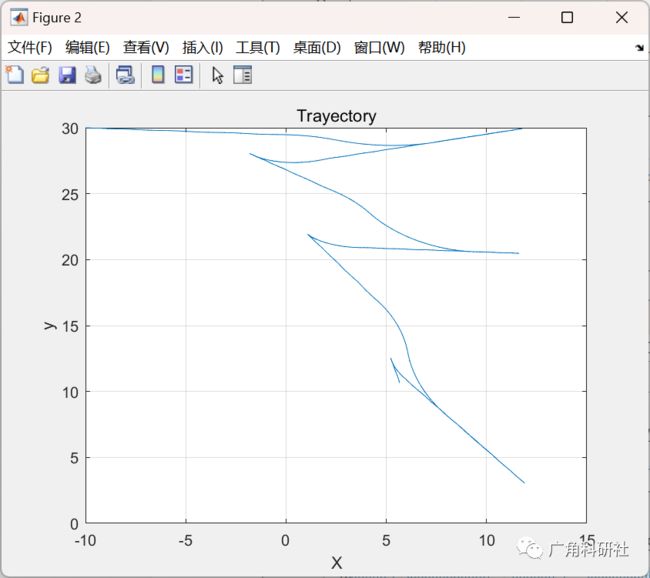
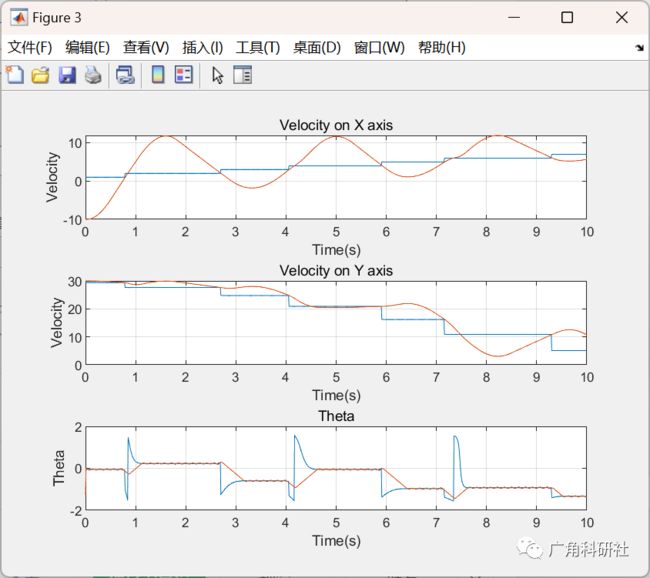
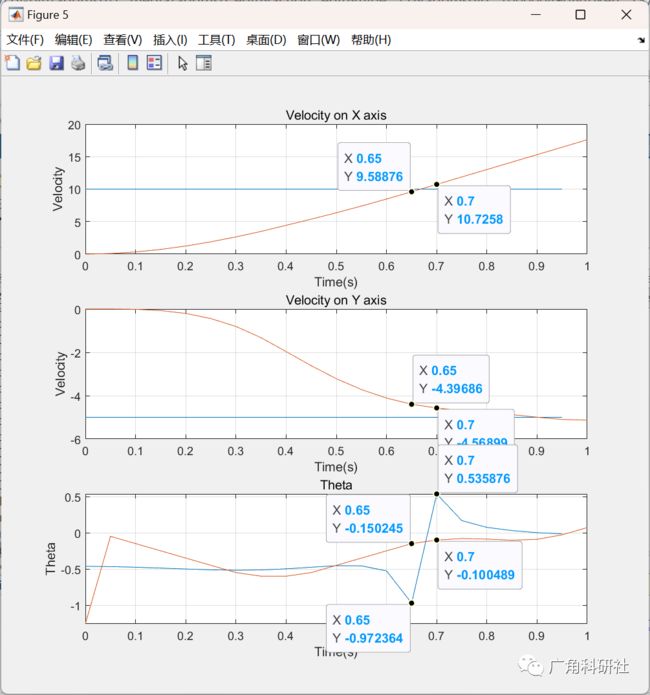
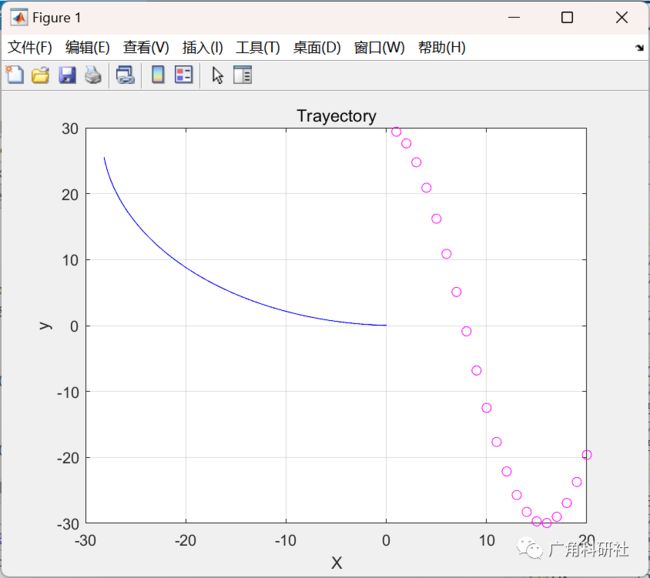
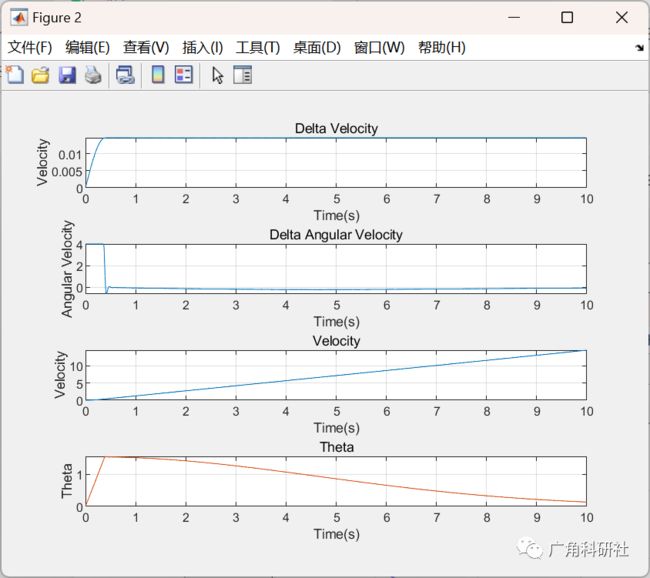
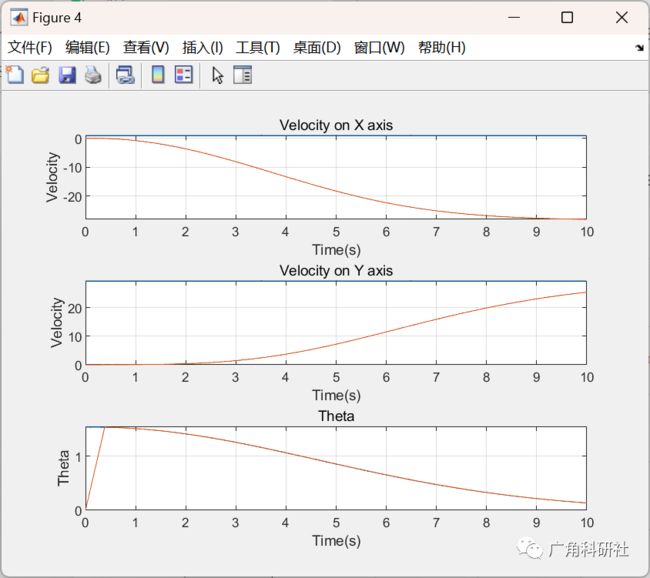
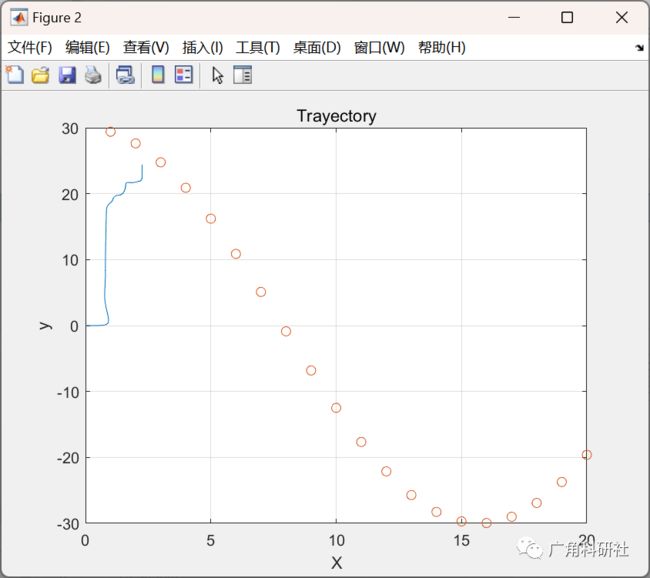
2 运行结果

主函数部分代码：

clc;
clear all;
close all;
% Initial state x(0)
X0=[0;0;(0*pi)/180];
%X0 =[2.3917 ;-1.3973;-1.2586];
vk=0;
Ts=0.005;
%thetak=(120*pi)/180;
thetak=-1.2586;
wk=0;
D=zeros(3,1);
N=50;
Xr=[-2 10 atan(1)]';
% Xr(3)=(atan((-50-X0(2))/(50-X0(1))));
% Xr(3)=(atan((Xr(2)-X0(2))/(Xr(1)-X0(1))));
s=3;
Simlength=(s/Ts);       
​
% Define cost functionx| and expected disturbances
Q=[0.00001 0 0;0 1 0;0 0 100000000];
R=[0.01 0;0 100];
W=ones(1,N)';  % expected demand (this is just an example)
​
[A B C]=model_system(vk,thetak,Ts);
[Gx,Gu,Gw]=constants_mpc(A,B,D,N);
% Build R_hat
R_hat = kron(eye(N),R);
% Build Q_hat
Q_hat=kron(eye(N),Q);
​
% Constraints
Ax=[1 0 0;0 1 0;-1 0 0 ;0 -1 0];
bx=100*[150; 150;150; 150];
Au=[1 0;0 1 ;-1 0;0 -1];
bu=[2; 0.01; 0; 0.01];
​
% Transform into U constraints
Au_hat=kron(eye(N),Au);
bu_hat=kron(ones(N,1),bu);
Ax_hat=kron(eye(N),Ax);
bx_hat=kron(ones(N,1),bx);
​
% Aggregated U constraints
AU=[Ax_hat*Gu; Au_hat];
bU=[bx_hat-Ax_hat*Gx*X0-Ax_hat*Gw*W;bu_hat];
​
% MPC into action
Xhist=X0;
Uhist=[];
VK=vk;
THK=thetak;
Disturb= normrnd(0.5,1,Simlength+N,1); %Longer than simulation for prediction horizon
% Simulation loop
XR=[];
% figure();
% plot(Xhist(1,:),Xhist(2,:),'b')
% ylabel('y');
% xlabel('X');
% title('Trayectory');
% grid on;
% hold on;
for k=1:Simlength
    % expected disturbances (force that they are different)
    W=0*Disturb(k:k+N-1)+0*normrnd(0,0.2,N,1); 
    % Update controller matrices for current state and disturbances (H and Au are constant)
    [A B C]=model_system(vk,thetak,Ts);
    Xr(3)=(atan((Xr(2)-X0(2))/(Xr(1)-X0(1))));
    %Xr(3)=(atan((-50-X0(2))/(50-X0(1))));
    [H,F,AU,bU]=MPC_U(A,B,D,N,W,X0,Xr,Q_hat,R_hat,Au_hat,bu_hat,Ax_hat,bx_hat);
    UMPC=quadprog(2*H,2*F,AU,bU);
    XR=[XR Xr];
    % Apply only first component
    u=UMPC(1:size(B,2));
%     X1=linearModel(A,B,D,u,Disturb(k),X0);
    X1=nonlinearModel(D,u,Disturb(k),X0,thetak,wk,vk,Ts);
​
    vk=saturated(0,20,vk+u(1));
    wk=saturated(-1,1,wk+u(2));
    thetak=X1(3);
    X0=X1;
    VK=[VK vk];
    THK=[THK thetak];
    Xhist=[Xhist X0];
    Uhist=[Uhist u];
​
%     plot(Xhist(1,:),Xhist(2,:),'b')
%     ylabel('y');
%     xlabel('X');
%     title('Trayectory');
%     grid on;
%     hold on;
%     pause(0.1);
%     Xpredict=Gx*X0+Gu*UMPC+Gw*W;
%     Xp=Xpredict(1:3:end);
%     Yp=Xpredict(2:3:end);
%     THp=Xpredict(3:3:end);
%     plot(Xp,Yp,'R')
​
end

3 参考文献

​[1]张明路,丁承君,段萍.移动机器人的研究现状与趋势[J].河北工业大学学报,2004(02):110-115.

部分理论引用网络文献，若有侵权联系博主删除。