拿来就能用！Dijkstra 算法实现快递路径优化

作者 | 李秋键

责编 | 伍杏玲

出品 | AI科技大本营（ID:rgznai100）

近几年来，快递行业发展迅猛，其中的程序设计涉及到运送路径的最优选择问题，下面我们尝试模拟实现快递路径优化问题，假设为快递公司设计快递投递路线优化程序：

（1）每个市有中转分发点，有些城市之间有直通路线，有些没有直通路线；（2）城市间的运费计算公式为：距离*1；

（3）假设投递包裹的尺寸、重量都一样，每条运输线路有个运力上限（即只能运输多少个包裹）。

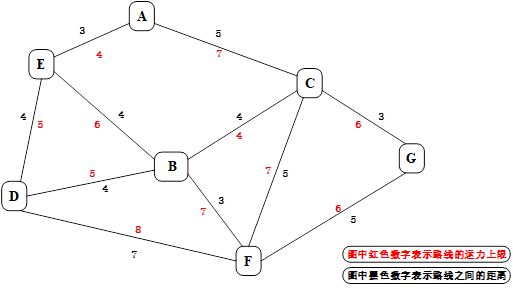
按照第（1）点要求，假设一共有7个城市，分别为A、B、C、D、E、F、G。

按照的第（2）点和第（3）点要求，假设各城市间满足的路线布局和费用，以及运力上限分别如下图所示：

实现的效果如下：

程序运行结果图（运力上限优化）

程序思路

(1) 建立各城市对象；

(2) 建立城市对象之间的关联，关联值包括四点（城市路径起点，城市路径终点，路径距离值，路径运力上限）。如城市A和城市B之间的关联值为[A,B,3,4]；

(3) 考虑到包裹尺寸、重量都是一样的，故假设其单位量都为1，即可以不用考虑。随机产生需要运输的当天包裹m个，产生的每个包裹对象的参量属性包括如下三点（包裹变量序号，包裹运输起点，包裹运输终点）。比如产生包裹1属性为[1,A,G]；

(4) 系统的可视化；

(5) 路径优化算法的设计。

基于上面分析，我们可以开始着手模拟设计“快递投递路线优化程序”，该系统主要包含三个基本模块：

1、总体框架程序，其中包括城市对象（城市路径起点，城市路径终点，路径距离值，路径运力上限），包裹对象（包裹变量序号，包裹运输起点，包裹运输终点），包裹数等基本参数设计；

2、可视化路径选择，将路径选择的结果输出后，按照基本的流程图形式进行全部输出；

3、优化算法设计，找到费用最低的路径方法。

数据结构设计

首先是程序预准备，包括定义宏、结构体。

参数定义：

这里定义城市最大数量为20。按照我们设定的7个城市，足够使用。

#define MAX_VERTEX_NUM 20

定义INFINITE，用来当做无穷大，即表示两个城市之间没有直接路线或达到运力上限直连路线作废。

#define INFINITE 10000 

图结构体的定义：

参数包括城市数vertexNum，城市名称vertex[MAX_VERTEX_NUM]数组，各城市路线距离值数组arc[MAX_VERTEX_NUM][MAX_VERTEX_NUM]，各城市路线运力上限数组limit[MAX_VERTEX_NUM][MAX_VERTEX_NUM]，各城市运力上限数组count[MAX_VERTEX_NUM][MAX_VERTEX_NUM]。

代码如下：

typedef struct 
{
    intvertexNum;
    charvertex[MAX_VERTEX_NUM];
    intarc[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
        intlimit[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
        intcount[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
}Graph,*PGraph;

存储距离和路径辅助结构体建立：

其中包括距离distance和路径数组path[MAX_VERTEX_NUM]。

代码如下：

//辅助数组中的元素定义
typedef struct
{
    int distance;
    int path[MAX_VERTEX_NUM];
}ArrayNode;

双向图的建立：

按照上文设定好的题目条件，建立双向网络，存储着城市属性，包括城市路线距离值arc参数、运力上限限流值limit参数、统计各路线已经使用的情况count参数。

代码如下：

void createdGraph(PGraph g) 
{ 
    int i,j; 
    g->vertexNum=7; 
    for(i=0;ivertexNum;i++) 
        g->vertex[i]='A'+i; 
    for(i=0;ivertexNum;i++) 
        for(j=0;jvertexNum;j++) 
            g->arc[i][j]=0; 
    for(i=0;ivertexNum;i++) 
        for(j=0;jvertexNum;j++) 
            g->limit[i][j]=0;
//这个属性是每条路的距离长度
    g->arc[0][4]=3; 
    g->arc[0][2]=5; 
    g->arc[1][2]=4; 
    g->arc[1][3]=4; 
    g->arc[1][4]=4; 
    g->arc[1][5]=3; 
    g->arc[2][5]=5; 
    g->arc[2][6]=3;
    g->arc[3][4]=4; 
    g->arc[3][5]=7; 
    g->arc[5][6]=5;
    //双向
    g->arc[2][0]=5;
    g->arc[2][1]=4;
    g->arc[3][1]=4;
    g->arc[4][0]=3;
    g->arc[4][1]=4;
    g->arc[4][3]=4;
    g->arc[5][1]=3;
    g->arc[5][2]=5;
    g->arc[5][3]=7;
    g->arc[6][2]=3;
    g->arc[6][5]=5;
//这个属性是每条路上的限流，即运力上限
    g->limit[0][4]=4; 
    g->limit[0][2]=7; 
    g->limit[1][2]=4; 
    g->limit[1][3]=5; 
    g->limit[1][4]=6; 
    g->limit[1][5]=7; 
    g->limit[2][5]=7; 
    g->limit[2][6]=6;
    g->limit[3][4]=5; 
    g->limit[3][5]=8; 
    g->limit[5][6]=6;
    g->limit[2][0]=7;
    g->limit[2][1]=4;
    g->limit[3][1]=5;
    g->limit[4][0]=4;
    g->limit[4][1]=6;
    g->limit[4][3]=5;
    g->limit[5][1]=7;
    g->limit[5][2]=7;
    g->limit[5][3]=8;
    g->limit[6][2]=6;
    g->limit[6][5]=6;
//这个属性是计算该条路走过了多少次，计数，判断会不会超过限流（运力上限），超过限流（运力上限）就把距离设成很大的数，即不考虑。初始情况下都是为0
    for(i=0;ivertexNum;i++) 
        for(j=0;jvertexNum;j++) 
            g->count[i][j]=0;
    g->count[0][4]=0; 
    g->count[0][2]=0; 
    g->count[1][2]=0; 
    g->count[1][3]=0; 
    g->count[1][4]=0; 
    g->count[1][5]=0; 
    g->count[2][5]=0; 
    g->count[2][6]=0;
    g->count[3][4]=0; 
    g->count[3][5]=0; 
    g->count[5][6]=0;
    g->count[2][0]=0;
    g->count[2][1]=0;
    g->count[3][1]=0;
    g->count[4][0]=0;
    g->count[4][1]=0;
    g->count[4][3]=0;
    g->count[5][1]=0;
    g->count[5][2]=0;
    g->count[5][3]=0;
    g->count[6][2]=0;
    g->count[6][5]=0;
}

算法设计

这里使用的算法是最短路径算法——Dijkstra。但考虑到路线的双向问题、限流问题等，需要对算法进行优化和修改。

算法描述

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)[1]，直到扩展到终点为止。

基本思想：

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)[2]。此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)[3]。初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”[4]。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径[5]。然后，再从U中找出路径最短的顶点，并将其加入到S中[6]；接着，更新U中的顶点和顶点对应的路径……重复该操作，直到遍历完所有顶点。

操作步骤：

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞[7]。

(2) 从U中选出”距离最短的顶点k”，并将顶点k加入到S中[8]；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离[9]。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离[10]；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点[11]。

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

最短路径算法代码：

（1）首先是计算from到各个顶点的直接距离，即初始化shortestPath数组：

for(i=0;ivertexNum;i++){ 
        if(from==i){ 
            shortestPath[i].distance=0; 
            shortestPath[i].path[0]=i; 
            flag[from]=1; 
        } 
        else if(g->arc[from][i]>0){ 
            shortestPath[i].path[0]=from; 
            shortestPath[i].path[1]=i; 
            shortestPath[i].distance=g->arc[from][i]; 
        }else 
            shortestPath[i].distance=INFINITE; 
    }

（2）然后每次求出一个最短路径：

while(nvertexNum){ 
        //选择shortestPath中距离最小的，求出from到这个顶点的最短路径 
        index=-1; 
        for(i=0;ivertexNum;i++){ 
            if(i==from) 
                continue; 
            if(flag[i]==0 && index==-1 && shortestPath[i].distance!=INFINITE) 
                index=i; 
            if(flag[i]==0 && index!=-1 && shortestPath[i].distancevertexNum;i++){ 
            if(i==from) 
                continue; 
            if(g->arc[index][i]>0 && g->arc[index][i]+shortestPath[index].distancearc[index][i]+shortestPath[index].distance; 
                //修改路径 
                j=0; 
                while(1){ 
                    shortestPath[i].path[j]=shortestPath[index].path[j]; 
                    if(shortestPath[index].path[j]==index) 
                        break; 
                    j++; 
                } 
                shortestPath[i].path[j+1]=i; 
            } 
        } 
        n++; 
    }

（3）输出结果：

printf("%c到%c的最短路径长度是：%d\n",from+'A',to+'A',shortestPath[to].distance); 
    printf("经过的顶点：  \n"); 
    i=0; 
    while(1){ 
        printf("%-3c\n",shortestPath[to].path[i]+'A'); 
        if(shortestPath[to].path[i]==to) 
            break; 
        i++; 
    } 
    printf("\n");

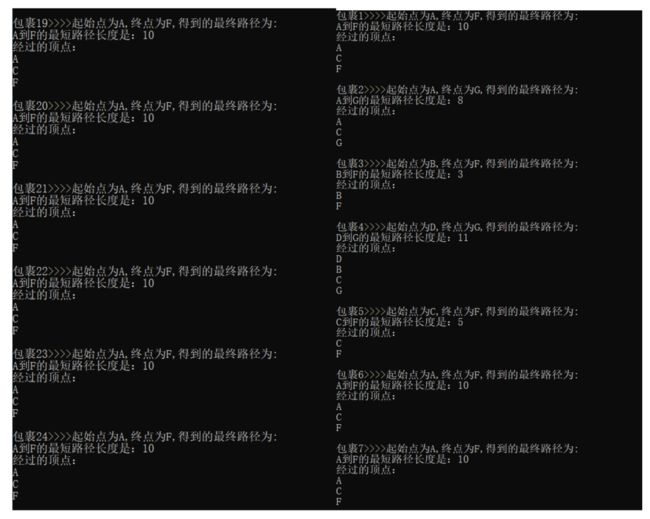
（4）程序主函数调用：这里设定的是产生25个包裹。包裹1为{1,A,F}，2为{2,A,G}，3为{3,B,F}，4为{4,D,G}，5为{5,C,F}；其他包裹都是从A到F。

void main() 
{ 
    int num=25;
    int k=0;
    Graph graph; 
    char from,to; 
    createdGraph(&graph); 
    //from为包裹起点城市，to为包裹终点城市;假设包裹1为{1,A,F}，2为{2,A,G}，3为{3,B,F}，4为{4,D,G}，5为{5,C,F}
    while(k>>>起始点为%c,终点为%c,得到的最终路径为:\n",k,from,to);
            Dijkstra(&graph,from-'A',to-'A'); 
        }
        else if(k==2){
            from='A';
            to='G'; 
            printf("包裹%d>>>>起始点为%c,终点为%c,得到的最终路径为:\n",k,from,to);
            Dijkstra(&graph,from-'A',to-'A'); 
        }
        else if(k==3){
            from='B';
            to='F'; 
            printf("包裹%d>>>>起始点为%c,终点为%c,得到的最终路径为:\n",k,from,to);
            Dijkstra(&graph,from-'A',to-'A'); 
        }
        else if(k==4){
            from='D';
            to='G'; 
            printf("包裹%d>>>>起始点为%c,终点为%c,得到的最终路径为:\n",k,from,to);
            Dijkstra(&graph,from-'A',to-'A'); 
        }
        else if(k==5){
            from='C';
            to='F'; 
            printf("包裹%d>>>>起始点为%c,终点为%c,得到的最终路径为:\n",k,from,to);
            Dijkstra(&graph,from-'A',to-'A'); 
        }
        else{
            from='A';
            to='F'; 
            printf("包裹%d>>>>起始点为%c,终点为%c,得到的最终路径为:\n",k,from,to);
            Dijkstra(&graph,from-'A',to-'A'); 
        }
    }

}

（5）结果展示：最终输出的结果就是没有考虑路线运力上限的输出结果：

程序运行结果图（未考虑运力上限优化）

上图可以明显的看出，运输第25次包裹时，从A运到F它还是选择了ACF路线。题目中设定的是A到C的运力上限只有5次，这里却走了AC路线高达20次，由此可见仅使用最短路径算法是不适应要求的，故下面将对算法加入限流条件进行优化。

算法优化

加入限流考虑，即运力上限，每条路只能走一定次数：

（1）首先初始化数组count，用来统计各个路线已经走过的次数。初始条件都为0，未走过一次：

//这个属性是计算该条路走过了多少次，计数，判断会不会超过限流（运力上限），超过限流（运力上限）就把距离设成很大的数，即不考虑。初始情况下都是为0
    for(i=0;ivertexNum;i++) 
        for(j=0;jvertexNum;j++) 
            g->count[i][j]=0;
    g->count[0][4]=0; 
    g->count[0][2]=0; 
    g->count[1][2]=0; 
    g->count[1][3]=0; 
    g->count[1][4]=0; 
    g->count[1][5]=0; 
    g->count[2][5]=0; 
    g->count[2][6]=0;
    g->count[3][4]=0; 
    g->count[3][5]=0; 
    g->count[5][6]=0;
    g->count[2][0]=0;
    g->count[2][1]=0;
    g->count[3][1]=0;
    g->count[4][0]=0;
    g->count[4][1]=0;
    g->count[4][3]=0;
    g->count[5][1]=0;
    g->count[5][2]=0;
    g->count[5][3]=0;
    g->count[6][2]=0;
    g->count[6][5]=0;

（2）判断每条路已使用过的次数是否超过限流（运力上限），如果超过了，就把路距离设为INFINITE，表示此条路不再考虑：

for(i=0;ivertexNum;i++) 
        for(j=0;jvertexNum;j++) 
            if (g->count[i][j]>g->limit[i][j] || g->count[j][i]>g->limit[j][i]){
            g->arc[i][j]=INFINITE; 
            g->arc[j][i]=INFINITE;
            }

（3）计数。每次选择最短路径的路线的各个支路都要加上1：因为路线是双向的，需要双向都加上1。

i=0; 
    while(1){ 
        //这条路被走过一次计数count就加上1
        //printf("%d",shortestPath[to].path[i]+0);
        printf("%-3c\n",shortestPath[to].path[i]+'A'); 
        if(shortestPath[to].path[i]==to) 
            break; 
//这条路被走过一次计数count就加上1
        g->count[shortestPath[to].path[i]+0][shortestPath[to].path[i+1]+0]+=1;
        g->count[shortestPath[to].path[i+1]+0][shortestPath[to].path[i]+0]+=1;
        i++; 
    }

（4）优化算法结果：

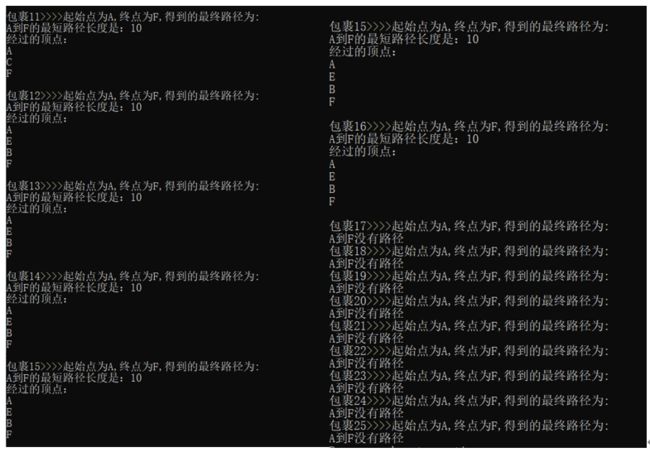
程序运行结果图（运力上限优化）

由上图发现，在考虑运力上限后，算法符合题目要求。同样是从A运到F目的地，AC这条路运力上限为5，我们看到包裹11走的是ACF，但是包裹12走的是AEBF，因为AC已经达到了运力上限，不能再走，故更换路线！

同理在包裹17后，AE这条路也达到了运力上限，已经没办法从A到F了，因为AC和AE这两条路都达到了运力上限，故程序找不到路线，符合设定的要求！

源码链接：https://pan.baidu.com/s/1iKlJ3At9mXpVmv3N8RQX0Q

提取码：0aib

作者简介：李秋键，CSDN博客专家，CSDN达人课作者。硕士在读于中国矿业大学，开发有taptap竞赛获奖等。

更多精彩推荐

☞30 周岁的 Python，“虐”我 20 年☞快过HugeCTR：用OneFlow轻松实现大型推荐系统引擎☞高手的习惯：pythonic风格代码☞对比四种爬虫定位元素方法，你更爱哪个？

点分享点收藏点点赞点在看