2020年第十一届C/C++ B组第一场蓝桥杯省赛真题
准备参加第十四届蓝桥杯,今天开始刷题目的第一天,下面是2020年第十一届C/C++ B组第一场蓝桥杯省赛真题,以下是我的做题目心得。
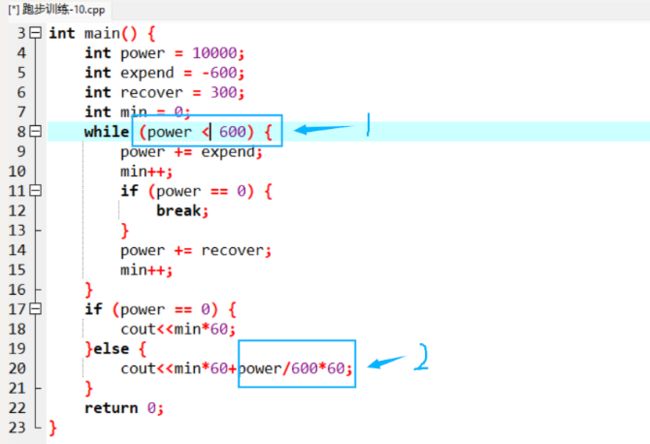
跑步训练
第一次写的代码失误点如下:第一个错误点是因为好久没有写代码,忘记判断对才能循环,算是失误。第二个点如果在现实中是对的,但是在代码里面会因为格式转换导致power/600变成0.这需要注意一下。
代码如下:
int main() {
int power = 10000;
int expend = -600;
int recover = 300;
int min = 0;
while (power > 600) {
power += expend;
min++;
if (power == 0) {
break;
}
power += recover;
min++;
}
if (power == 0) {
cout<纪念日
本题目我是从1921年开始计算的,而且我把算闰年的部分分开了。
计算闰年的判断如下:普通闰年:公历年份是4的倍数且不是100的倍数为普通闰年(如2004、2020年就是闰年)。
世纪闰年:公历年份是整百数的,必须是400的倍数才是世界闰年(如2000是世纪闰年,1900不是世纪闰年)。
因为是填空题,我写的代码并不是很好看,只是用于计算。
最后代码如下:
#include
using namespace std;
int main(){
int year = 2020 - 1921;//年数
int m = (2020 - 1924) / 4 + 1;//闰年数
int day = year * 365 + m -22; //天数
cout< 合并检测
本题目没有告诉我们A国的人数,这一开始就有点没有头绪,然后我们可以从感染率为1入手,毕竟代表人的数字不能是小数,那我就设A国总人数为100,这样简单也方便。那感染的人就只有一个。设试管的使用量为sum,可以得下面的试子:
A国人数可被k整除:sum=100/k+k
A国人数不能被k整除:sum=100/k+k+1
最后代码如下:
#include
using namespace std;
int main()
{
int k = 0;
int sum = 0x3f3f3f;//试管数量
for(int i = 1; i <= 100; i++){
if(100%i==0)
{
if(100/i+i REPEAT程序
我们可以看看题目的对应方式,可以发现有点像for循环,其中REPEAT后面的数字就代表要循环的次数而且A=A+5循环了60次,说明它是最里面的命令行。
代码如下:
#include
using namespace std;
int main() {
int A = 0;
for (int i = 0;i < 2;i ++) {
A += 4;
for (int j = 0;j < 5;j ++) {
for (int k = 0;k < 6;k ++) {
A += 5;
}
A += 7;
}
A += 8;
}
A += 9;
cout << A < 矩阵
这个题目需要使用动态规划的知识,其中动态规划的知识可以分三步走:
第一步,定义一个数组元素的定义,我定义一个dp[i][j]的数组,i代表放在第一行的数字量,j代表第二行的数字量。
因为是2×1010的矩阵,所以每一行的最大数字量为1010.
第二步,找出数组元素之间的关系式:
将当前数放在第一行:dp[i][j] += dp[i - 1][j],将当前数放在第二行:dp[i][j] += dp[i][j - 1]
第三步,得找到一个初始值.比如在矩阵里面不放数字,也是一种方案,故dp[0][0]=1
最后代码如下:
#include
using namespace std;
int dp[1011][1011];
int main() {
dp[0][0]=1;
for(int i = 0;i <= 1010;i ++) {
for(int j = 0;j <= 1010;j ++) {
if(i-1 >= j) {
dp[i][j] += dp[i-1][j] % 2020;
}
if(j) {
dp[i][j] += dp[i][j-1] % 2020;
}
}
}
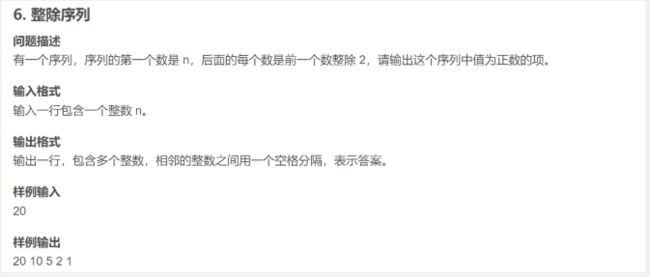
cout<< dp[1010][1010] < 整除序列
这个题目使用while语句即可完成,而且最好不用存在数组里面,直接得答案后就输出
代码如下:
#include
using namespace std;
int main() {
int num;
cin>>num;
cout< 1) {
num =num/2;
cout< 解码
这个题目只要会使用string库就可以解出来了
代码如下:
#include
#include
using namespace std;
int main () {
string st;
cin>>st;
for(int i = 0;i < st.length();i ++) {
if (st[i] > 48 && st[i] < 58) {
for(int j = 1;j < st[i]-48;j ++) {
cout< 走方格
这个还是使用的是动态规划,加一个小的限制就是m和n不能同时为偶数,但是这个并不重要,我们直接分析,三步走。
第一步,定义一个数组。dp[i][j],带表它走到的位置需要花费的方案。
第二步,找出数组元素之间的关系式:dp[i][j]=dp[i-1][j]+dp[i][j-1]
第三步,找出初始值。因为它只能向右或者向下,这样的话可以初始以下两方面:
dp[0] [0….n-1] = 1; // 相当于最上面一行,只能一直往左走
dp[0…m-1] [0] = 1; // 相当于最左面一列,只能一直往下走
代码如下:
#include
using namespace std;
int dp[31][31];
int count(int m,int n);
int main(){
int m,n;
cin>>m>>n;
if(!(m % 2 |n % 2)) {
cout<<0;
}else {
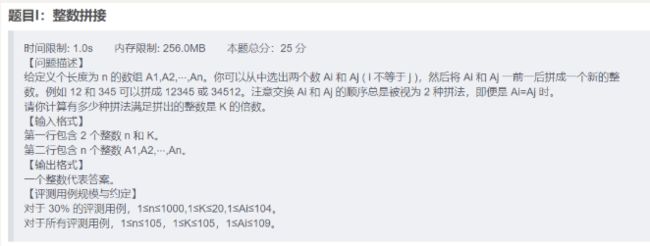
cout< 整数拼接
一开始想的是把数字变成字符串,后面拼接后再改成数字,但是这样太麻烦,我也不会,那我们可以求它的位数,用次方的方式来使他变成拼接的前半部分。思路清晰后代码如下:
#include
#include
using namespace std;
int figure(int num); //求位数
int main() {
int n,k;
int count = 0;
int num;
cin>>n>>k;
int a[n];
for(int i = 0;i < n;i ++) {
cin>>a[i];
}
for(int i = 0;i < n;i ++) {
for(int j = 0;j < n;j ++) {
if(i == j) {
continue;
}
num = a[i]*pow(10,figure(a[j]))+a[j];//这样可以直接加在后面
if(num % k == 0) {
count++;
}
}
}
cout< 网络分析
我看见这个题目需要使用的知识点是图的知识点,由于可以相互通讯,那就是无向连接,由于它是需要遍历的,那我们可以思考一下DFS与BFS算法相关知识。我使用邻接矩阵来存储。
代码如下:
#include
#include
using namespace std;
int main() {
int n,m,top;
cin>>n>>m;
queue myqueue;
int a[n][n];//邻接矩阵
int b[n][n];
for (int i = 0;i < n;i ++) {
for (int j = 0;j < n;j ++) {
a[i][j] = 0;
}
}
for (int i = 0;i < n;i ++) {
for (int j = 0;j < n;j ++) {
b[i][j] = 0;
}
}
int m1,m2,m3;//判断的数字
for (int i = 0;i < m;i ++) {
cin>>m1>>m2>>m3;
if (m1 == 1) {
a[m3-1][m2-1] = 1;
a[m2-1][m3-1] = 1;
}
if (m1 == 2) {
myqueue.push(m2);
while(myqueue.size()) {
top = myqueue.front();
a[top-1][top-1] += m3;
myqueue.pop();
for(int j = 0;j < n;j ++) {
if(a[top-1][j] == 1) {
if(b[top-1][j] == 1) {
continue;
}
b[top-1][j] = 1;
b[j][top-1] = 1;
myqueue.push(j+1);
}
}
}
for (int i = 0;i < n;i ++) {
for (int j = 0;j < n;j ++) {
b[i][j] = 0;
}
}
}
}
for (int i = 0;i < n;i ++) {
for (int j = 0;j < n;j ++) {
cout< 第十题的代码是错误的,我还在改正,后面对了,我会重新修改发布。希望有小伙伴可以与我探讨一下思路,大家一起分享,一起进步!!!