100天精通Python（可视化篇）——第84天：matplotlib绘制不同种类炫酷直方图参数说明+代码实战（普通、多变量、堆叠、分组、多个子图、折线、曲线直方图）

专栏导读

本文已收录于《100天精通Python从入门到就业》：本专栏专门针对零基础和需要进阶提升的同学所准备的一套完整教学，从0到100的不断进阶深入，后续还有实战项目，轻松应对面试，专栏订阅地址：https://blog.csdn.net/yuan2019035055/category_11466020.html

• 优点：订阅限时9.9付费专栏进入千人全栈VIP答疑群，作者优先解答机会（代码指导、远程服务），群里大佬众多可以抱团取暖（大厂内推机会）
• 专栏福利：简历指导、招聘内推、每周送实体书、80G全栈学习视频、300本IT电子书：Python、Java、前端、大数据、数据库、算法、爬虫、数据分析、机器学习、面试题库等等
  
  

1. 直方图介绍

1）介绍

直方图(Histogram)，又称质量分布图，是一种统计报告图，由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类型，纵轴表示分布情况。可以将一组数据中的频率或频数汇总显示在一个图表上，以频率柱的形式表示数据的比例和分布。

特点

• 更直观的展示数据分布
• 易于比较数据之间的差异
• 易于发现数据中的极端值
• 可以更直观地发现正态分布、非正态分布以及偏态分布

应用场景

• 分析客户行为、特征分布
• 分析产品特征、卖点
• 分析市场份额
• 分析需求量

2）直方图的五种形态

（1）标准型

标准型直方图的特点是：

• 区间宽度相等：每个区间的宽度应该相等，这样才能保证直方图的准确性。

• 矩形高度表示频率或密度：每个矩形的高度应该表示该区间内数据的频率或密度，这样才能反映出数据的分布情况。

• 相邻矩形相连：相邻的矩形应该相连，这样才能形成连续的直方图。

• 坐标轴标注清晰：坐标轴应该标注清晰，包括横轴表示数据范围，纵轴表示频率或密度。

（2）孤岛型

在直方图旁边有孤立的小岛出现，当这种情况出现时过程中有异常原因：

（3）双峰型

当直方图中出现了两个峰，这是由于观测值来自两个总体、两个分布的数据混合在一起造成的：

（4）折齿型

当直方图出现凹凸不平的形状，这是由于作图时数据分组太多，测量仪器误差过大或观测数据不准确等造成的，此时应重新收集数据和整理数据：

（5）陡壁型

当直方图像高山的陡壁向一边倾斜时，通常表现在产品质量较差时，为了符合标准的产品，需要进行全数检查，以剔除不合格品：

3）参数说明

在matplotlib中，使用plt.hist()函数可以绘制直方图。该函数的主要参数如下：

plt.hist(x, bins=None, range=None, density=None, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, color=None, label=None, stacked=False, alpha=None, edgecolor=None, linewidth=None, xticks=None, yticks=None, **kwargs)

常用参数的说明如下：

• x：需要绘制直方图的数据，可以是一个数组或序列。
• bins：指定直方图的条形数，或者指定每个条形的边界值。默认值为10。
• range：指定直方图的范围，即x轴的取值范围。默认值为None，表示使用数据的最大值和最小值作为范围。
• density：指定是否将直方图归一化。默认值为None，表示不进行归一化。
• cumulative：指定是否绘制累计直方图。默认值为False。
• histtype：指定直方图的类型，可以是’bar’、‘barstacked’、‘step’、‘stepfilled’。默认值为’bar’。
• align：指定直方图条形的对齐方式。默认值为’mid’，表示条形的中心与x轴上的标签对齐。
• orientation：指定直方图的方向，可以是’horizontal’或’vertical’。默认值为’vertical’。
• color：指定直方图的颜色。
• label：指定直方图的标签。
• alpha：指定直方图的透明度。
• edgecolor：指定直方图条形边缘的颜色。
• linewidth：指定直方图条形边缘的宽度。
• xticks、yticks：指定x轴、y轴上的刻度值。

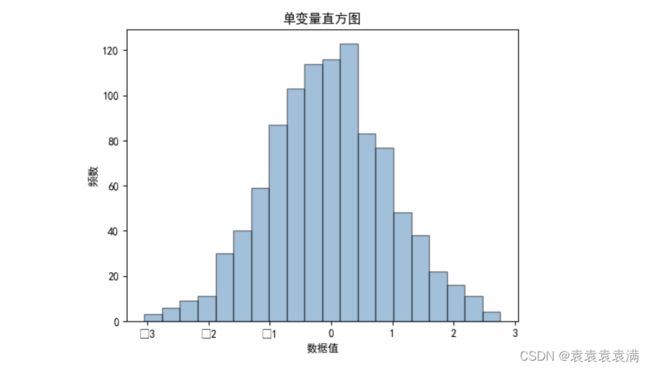
2. 单变量直方图

单变量直方图用于绘制一个变量的频率分布情况，可以使用plt.hist()函数绘制：

import matplotlib.pyplot as plt
import numpy as np
from pylab import mpl

# 展示中文字体
mpl.rcParams['font.sans-serif'] = ['SimHei'] 

# 生成数据
np.random.seed(0)
x = np.random.randn(1000)

# 绘制直方图
plt.hist(x, bins=20, alpha=0.5, color='steelblue', edgecolor='black')

# 添加标题和坐标轴标签
plt.title('单变量直方图')
plt.xlabel('数据值')
plt.ylabel('频数')

# 显示图形
plt.show()

代码解释：

使用numpy.random.randn()生成1000个随机数作为数据。
使用plt.hist()函数绘制直方图，指定bins为20，alpha为0.5，颜色为steelblue，边缘颜色为black。
使用plt.title()、plt.xlabel()和plt.ylabel()添加标题和坐标轴标签。
使用plt.show()显示图形。

运行结果：

3. 多变量直方图

多变量直方图用于绘制两个变量的关系，可以使用plt.hist2d()函数绘制：

import matplotlib.pyplot as plt
import numpy as np
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 生成数据
np.random.seed(0)
x = np.random.randn(1000)
y = np.random.randn(1000)

# 绘制直方图
plt.hist2d(x, y, bins=20, cmap='Blues')

# 添加标题和坐标轴标签
plt.title('多变量直方图')
plt.xlabel('x')
plt.ylabel('y')

# 添加颜色条
plt.colorbar()

# 显示图形
plt.show()

代码解释：

使用numpy.random.randn()生成1000个随机数作为x和y的数据。
使用plt.hist2d()函数绘制直方图，指定bins为20，颜色映射为Blues。
使用plt.title()、plt.xlabel()和plt.ylabel()添加标题和坐标轴标签。
使用plt.colorbar()添加颜色条。
使用plt.show()显示图形。

运行结果：

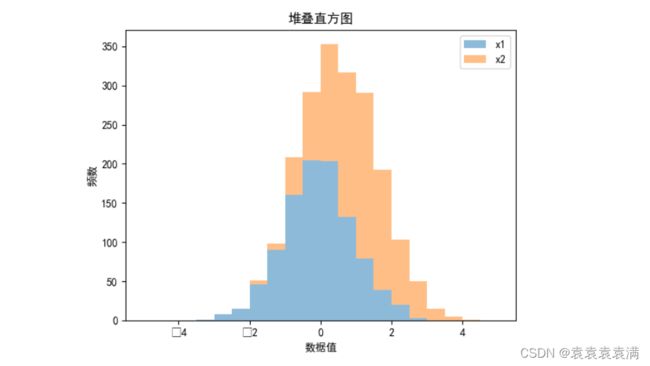
4. 堆叠直方图

堆叠直方图用于比较两个或多个变量的频率分布情况，可以使用plt.hist()函数结合numpy.histogram()函数绘制：

import matplotlib.pyplot as plt
import numpy as np
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 生成数据
np.random.seed(0)
x1 = np.random.randn(1000)
x2 = np.random.randn(1000) + 1

# 计算直方图数据
bins = np.linspace(-5, 5, 21)
hist1, _ = np.histogram(x1, bins=bins)
hist2, _ = np.histogram(x2, bins=bins)

# 绘制堆叠直方图
plt.hist([x1, x2], bins=bins, stacked=True, alpha=0.5, label=['x1', 'x2'])

# 添加标题和坐标轴标签
plt.title('堆叠直方图')
plt.xlabel('数据值')
plt.ylabel('频数')

# 添加图例
plt.legend()

# 显示图形
plt.show()

代码解释：

使用numpy.random.randn()生成1000个随机数作为x1和x2的数据。
使用numpy.linspace()生成21个等距的数作为bins。
使用numpy.histogram()函数分别计算x1和x2的直方图数据。
使用plt.hist()函数绘制堆叠直方图，指定bins为bins，alpha为0.5，标签为'x1'和'x2'。
使用plt.title()、plt.xlabel()和plt.ylabel()添加标题和坐标轴标签。
使用plt.legend()添加图例。
使用plt.show()显示图形。

运行结果：

5. 分组直方图

分组直方图用于比较不同组之间的频率分布情况，可以使用plt.hist()函数结合numpy.histogram()函数绘制：

import matplotlib.pyplot as plt
import numpy as np
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 生成数据
np.random.seed(0)
x1 = np.random.randn(1000)
x2 = np.random.randn(1000) + 1

# 计算直方图数据
bins = np.linspace(-5, 5, 21)
hist1, _ = np.histogram(x1, bins=bins)
hist2, _ = np.histogram(x2, bins=bins)

# 绘制分组直方图
width = 0.4
plt.bar(bins[:-1], hist1, width=width, align='edge', alpha=0.5, label='x1')
plt.bar(bins[:-1]+width, hist2, width=width, align='edge', alpha=0.5, label='x2')

# 添加标题和坐标轴标签
plt.title('分组直方图')
plt.xlabel('数据值')
plt.ylabel('频数')

# 添加图例
plt.legend()

# 显示图形
plt.show()

代码解释：

使用numpy.random.randn()生成1000个随机数作为x1和x2的数据。
使用numpy.linspace()生成21个等距的数作为bins。
使用numpy.histogram()函数分别计算x1和x2的直方图数据。
使用plt.bar()函数绘制分组直方图，指定宽度为0.4，对齐方式为'edge'，标签为'x1'和'x2'。
使用plt.title()、plt.xlabel()和plt.ylabel()添加标题和坐标轴标签。
使用plt.legend()添加图例。
使用plt.show()显示图形。

运行结果：

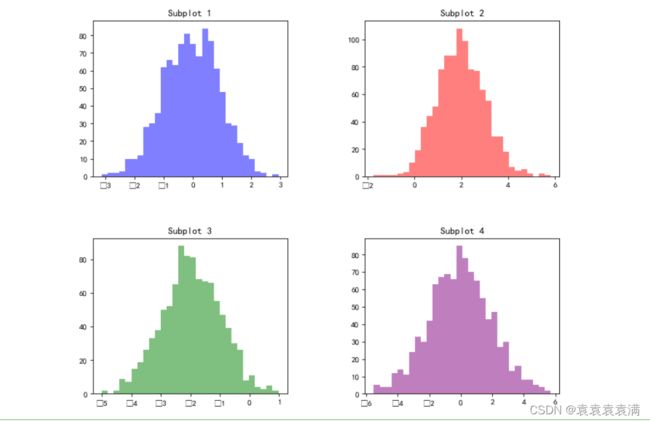
6. 多个子图的直方图

下面是一个示例代码，它使用matplotlib库绘制了一个2x2的子图，每个子图都是一个直方图。

import matplotlib.pyplot as plt
import numpy as np

# 生成随机数据
data1 = np.random.normal(0, 1, 1000)
data2 = np.random.normal(2, 1, 1000)
data3 = np.random.normal(-2, 1, 1000)
data4 = np.random.normal(0, 2, 1000)

# 设置图像大小和分辨率
fig = plt.figure(figsize=(10, 8), dpi=80)

# 绘制第一个子图
ax1 = fig.add_subplot(2, 2, 1)
ax1.hist(data1, bins=30, alpha=0.5, color='blue')
ax1.set_title('Subplot 1')

# 绘制第二个子图
ax2 = fig.add_subplot(2, 2, 2)
ax2.hist(data2, bins=30, alpha=0.5, color='red')
ax2.set_title('Subplot 2')

# 绘制第三个子图
ax3 = fig.add_subplot(2, 2, 3)
ax3.hist(data3, bins=30, alpha=0.5, color='green')
ax3.set_title('Subplot 3')

# 绘制第四个子图
ax4 = fig.add_subplot(2, 2, 4)
ax4.hist(data4, bins=30, alpha=0.5, color='purple')
ax4.set_title('Subplot 4')

# 调整子图之间的距离和位置
plt.subplots_adjust(left=0.1, bottom=0.1, right=0.9, top=0.9, wspace=0.4, hspace=0.4)

# 显示图像
plt.show()

代码中使用了numpy库生成了4组随机数据，然后使用matplotlib库创建了一个大小为10x8、分辨率为80的图像。接着，使用add_subplot()方法在图像上创建了4个子图，并分别将随机数据绘制成直方图。最后，使用subplots_adjust()方法调整了子图之间的距离和位置，使它们更加美观。最后，使用show()方法显示图像。

运行结果：

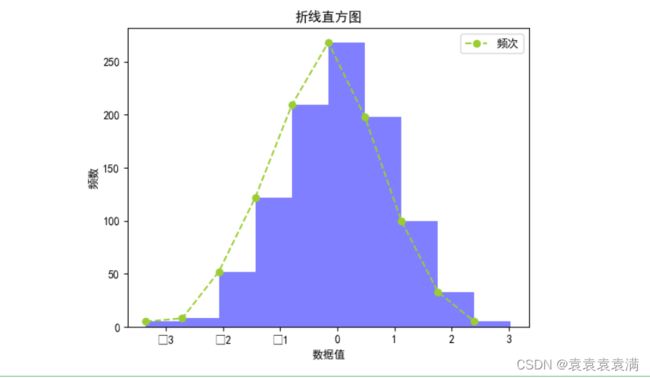
7. 折线直方图

在直方图中，我们也可以加一个折线图，辅助我们查看数据变化情况

import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 生成随机数据
data  = np.random.normal(0, 1, 1000)

# 创建Axes对象
fig,ax = plt.subplots()

# 绘制直方图
n,bins_num,pat = ax.hist(data,bins=10,alpha=0.5, color='blue') 
 
# 绘制折线图
ax.plot(bins_num[:10],n,marker = 'o',color="yellowgreen",linestyle="--")

# 添加标题和坐标轴标签
plt.title('折线直方图')
plt.xlabel('数据值')
plt.ylabel('频数')

# 添加图例
plt.legend(labels=['频次'])

# 展示图像
plt.show()

代码解释：

首先通过pyplot.subplot()创建Axes对象

通过Axes对象调用hist()方法绘制直方图，返回折线图所需要的下x,y数据

然后Axes对象调用plot()绘制折线图

运行结果：

8. 正态分布曲线直方图

下面是一个示例代码，它使用matplotlib库绘制了一个曲线拟合直方图

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
from scipy.optimize import curve_fit
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 生成随机数据
data = np.random.normal(0, 1, 1000)

# 绘制直方图
n, bins, patches = plt.hist(data, bins=30, density=True, alpha=0.5, color='blue')

# 定义拟合函数
def fit_function(x, mu, std, a):
    return a * norm.pdf(x, mu, std)

# 初始拟合参数
mu, std = norm.fit(data)
a = 1

# 拟合曲线
popt, pcov = curve_fit(fit_function, bins[:-1], n, p0=[mu, std, a])
x = np.linspace(bins[0], bins[-1], 100)
plt.plot(x, fit_function(x, *popt), 'r-', linewidth=2)

# 设置图像标题和坐标轴标签
plt.title('曲线拟合直方图')
plt.xlabel('数据值')
plt.ylabel('频数')

# 显示图像
plt.show()

代码解释：

代码中使用了numpy库生成了1000个符合正态分布的随机数据，然后使用matplotlib库的hist()方法将这些数据绘制成直方图，并设置了bins为30，density为True表示绘制的是概率分布直方图，alpha为0.5表示设置透明度为0.5，color为blue表示设置颜色为蓝色。同时，返回了直方图的数值、区间和补丁。

接着，定义了一个拟合函数fit_function，它使用了norm.pdf()方法计算了正态分布的概率密度函数，并乘以一个系数a，用于调整拟合曲线的幅度。然后，使用scipy库的curve_fit()方法拟合了直方图的数据，并生成了100个均匀分布的数据，用于绘制拟合曲线。最后，使用matplotlib库的plot()方法绘制了拟合曲线，并使用title()、xlabel()和ylabel()方法设置了图像的标题和坐标轴标签。

图像中展示了随机数据的曲线拟合情况，蓝色的直方图表示随机数据的分布情况，红色的曲线是拟合曲线。拟合曲线是通过拟合函数fit_function和直方图的数据计算得出的，它可以更好地描述随机数据的分布情况。

运行结果：

9. 核密度曲线直方图

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from sklearn.neighbors import KernelDensity
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']

# 生成随机数据
np.random.seed(123)
data = np.random.normal(loc=0, scale=1, size=1000)

# 计算正态分布概率密度函数的值
x = np.linspace(-4, 4, 100)
pdf = norm.pdf(x)

# 计算核密度估计的值
kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(data.reshape(-1, 1))

# 计算正态分布估计的值
log_dens = kde.score_samples(x.reshape(-1, 1))
dens = np.exp(log_dens)

# 绘制直方图和曲线
fig, ax = plt.subplots()
ax.hist(data, bins=30, density=True, alpha=0.5, color='blue')
ax.plot(x, pdf, 'r-', label='正态分布曲线')
ax.plot(x, dens, 'g--', label='核密度曲线')
ax.legend()
plt.show()

代码解释：

在这个代码中，我们首先使用numpy生成了一个长度为1000的随机数据，然后使用scipy.stats.norm计算了正态分布的概率密度函数的值，并使用sklearn.neighbors.KernelDensity计算了核密度估计的值。接着，我们使用matplotlib绘制了直方图和两个曲线，其中正态分布曲线的颜色为红色实线，核密度曲线的颜色为绿色虚线。最后，我们使用plt.show()方法显示了图形。

运行结果：

正态分布曲线和核密度曲线的区别和应用场景如下：

• 正态分布曲线，也称为高斯分布曲线，是一种连续性分布函数，通常用于描述数据集中度和散布度。正态分布曲线具有钟形对称的形状，其参数由均值和标准差确定。正态分布曲线在统计学中有广泛的应用，例如在假设检验、置信区间估计、回归分析等方面。

• 核密度曲线则是一种非参数估计方法，用于估计概率密度函数。核密度曲线的形状取决于所选用的核函数，通常使用高斯核函数。核密度曲线可以用于描述数据分布的形状和密度，也可以用于比较两个数据集之间的差异。在数据挖掘、模式识别、图像处理等领域中，核密度估计方法被广泛应用。

• 正态分布曲线和核密度曲线都可以用于描述数据的分布情况，但在应用场景上有所不同。正态分布曲线通常用于描述连续性变量的分布，例如身高、体重、考试成绩等。而核密度曲线则更适用于描述离散性变量的分布，例如文本中词语出现的频率、图像中像素值的分布等。