线性回归从零开始实现

准备数据

根据带有噪声的线性模型构造一个人造数据集，线性模型参数=[2,−3.4]⊤，=4.2和噪声项生成数据集及其标签：

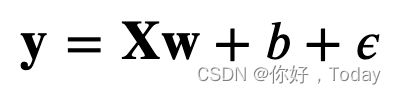
数据生成

def synthetic_data(w, b, num_examples):  
    """生成 y = Xw + b + 噪声。"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

数据解读：features 中的每一行都包含一个二维数据样本，labels 中的每一行都包含一维标签值（一个标量）

print('features:', features[0], '\nlabel:', labels[0])

features: tensor([-0.6612, -1.8215])
label: tensor([9.0842])

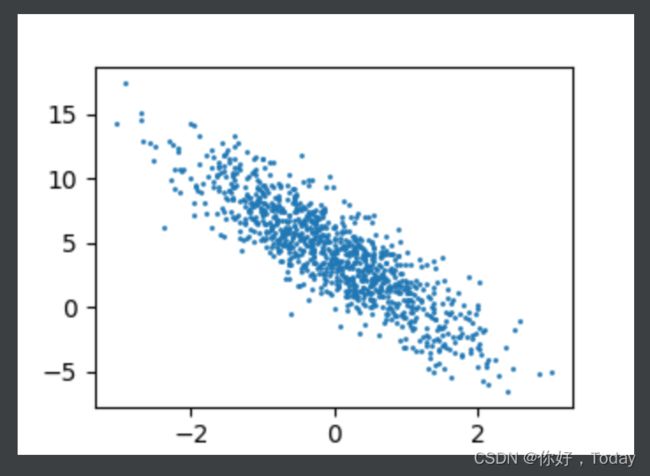
数据图示：

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
plt.show()

注：d2l是李沐动手学深度学习里面的一个包，可以通过pip install d2l直接安装

数据处理

定义一个data_iter 函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

模型

初始化模型参数

w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

定义模型

def linreg(X, w, b):  
    """线性回归模型。"""
    return torch.matmul(X, w) + b

定义损失函数

def squared_loss(y_hat, y):  
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2

定义优化算法：小批量随机梯度下降优化器

def sgd(params, lr, batch_size):  
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

训练过程

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)
        l.sum().backward()
        sgd([w, b], lr, batch_size)
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

比较真实参数和通过训练学到的参数来评估训练的成功程度

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

完整代码

# %matplotlib inline 注释掉此行
import random
import torch
import matplotlib.pyplot as plt  # 增加此行
from d2l import torch as d2l


# 生成人工数据集
def synthetic_data(w, b, num_examples):
    """生成 y = Xw + b + 噪声。"""
    X = torch.normal(0, 1, (num_examples, len(w)))  # 从均值为0，标准差为1的正太分布中，提取生成 num_examples * len(w)) 的Tensor
    y = torch.matmul(X, w) + b  # torch.matmul是tensor的乘法
    y += torch.normal(0, 0.01, y.shape)  # 加噪音
    return X, y.reshape((-1, 1))


true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

print('features:', features[0], '\nlabel:', labels[0])

d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
plt.show()


# 生成大小为batch_size的小批量
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

batch_size = 10
#
# for X, y in data_iter(batch_size, features, labels):
#     print(X, '\n', y)
#     break


w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)


def linreg(X, w, b):
    """线性回归模型。"""
    return torch.matmul(X, w) + b


def squared_loss(y_hat, y):
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2


def sgd(params, lr, batch_size):
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()


lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)
        l.sum().backward()
        sgd([w, b], lr, batch_size)
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

总结

线性回归模型的从零开始实现