学习matlab（十八）——小波分析

  小波分析克服了短时傅里叶变换在单分辨率上的缺陷，具有多分辨率分析的特点。下面对小波分析的基本理论进行介绍,包括连续小波变换、离散小波变换、多分辨分析和小波包分析,最后介绍在小波分析中常用的小波。
  小波变换采用随频率的时间-频率窗口，是进行信号时频分析和处理的理想工具。在利用小波分析信号分析时，在低频部分采用较低的时间分辨率,提高频率分辨率;在高频部分,采用较低的频率分辨率来换取精确的时间定位。小波包分解与小波分解相比，是一种更精细的分解方法，不仅对低频部分进行分解，对高频部分也进行分解。
  小波变换速度快，适合信号的在线分析。小波分析能够通过变换充分突出问题某些方面的特征，因此，小波变换在许多领域都得到了成功的应用。
小波变换的实质是将信号在一个时域和频域上均具有局部化性质的平移伸缩小波权函数进行卷积,从而将信号分解成位于不同时间和频率上的各个成份。满足允许条件:

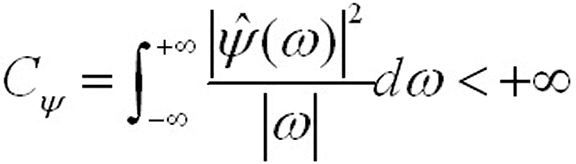
  离散小波变换（ discrete wavelet transform,DWT)是指对尺度因子a和平移因子b进行离散化,而不是时间的离散化。离散小波变换的一个重要问题是如何降低计算量和数据量，因为如果对尺度因子a和平移因子b离散的间隔小,那么计算量和数据量都是相当惊人的。
  离散小波变换的一个突破性成果是Mallat于1989年在多分辨分析的基础上提出的快速算法:Mallat算法Mallat享法在小波分析中的作用相当于快速傅立叶变换（ FFT)在傅立叶分析中的作用。Mallat算法由小波滤波器H、G和h、g对信号进行分解和重构。Mallat分解算法为

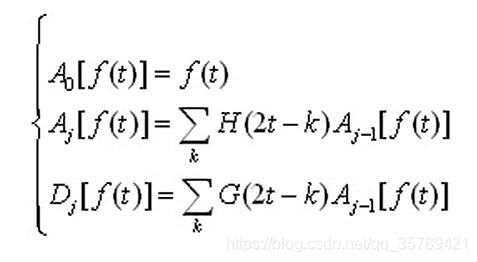
  对信号f(t)进行离散小波的3层分解,近似系数和细节系数。

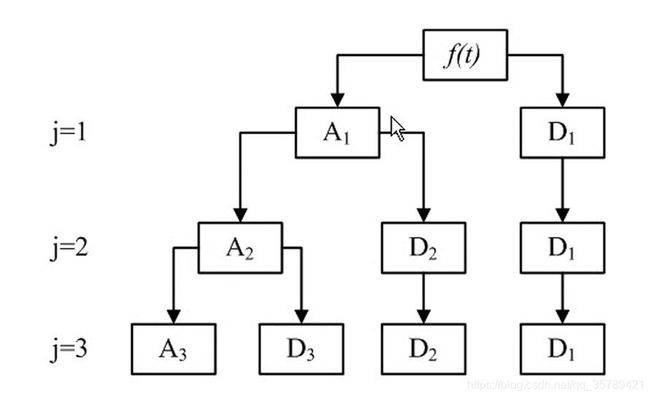
  在MATLAB的命令行窗口输入:help wavelet，可以查询MATLAB的小波工具箱中的所有函数,以及小波工具箱,的版本。在MATLAB 2010a中小波工具箱的版本为4.5。用户在命令行窗口输入;wavedemo可以查看例子程序。采用函数wavemngr()可以获取所有的小波。通过函数waveinfo()可以获取小波的信息。

1.分解和重构

  在MATLAB中,采用函数cwt()进行一维连续小波分解,该函数的常用调用格式为:coefs=cwt(s,scales, ‘wname’):该函数对信号s进行尺度为scales的连续小波分解,小波为wname,返回值coefs为系数。coefs=cwt(s, scales, ‘wname’, ‘plot’):该函数通过参数plot显示变换后的图形。
  在MATLAB中,采用函数dwt()进行一维小波的单层分解,该函数的常用调用格式为:[cA,cD]=dwt(X, ‘wname’):该函数采用小波wname进行单层分解，cA为近似系数,cD为细节系数。[cA, cD]=dwt(x,‘Wname’, ‘mode’，MODE):该函数设定扩展模式为MODE.在MATLAB中,采用函数wavdec()进行一维小波的多层分解。
  在MATLAB中，利用函数idwt()进行单层小波重构,该函数的调用格式为:X=idwt(cA, cD, ‘wname’),cA为近似系数,cD为细节系数,wname为采用的小波。利用函数waverec()进行多层小波的重构。在进行小波的重构时,小波的类型必须和分解时保持一致。

2.小波分解和重构

  二维小波非常适合进行图像的分析和处理。图像的单层二维小波分解,将图像分解为4个原图1/4大小的图像,左上的图像为两个维度都采用低通滤波后的结果;右上的图像为横向采用低通滤波,纵向采用高通滤波后的结果;左下的图像为横向采用高通滤波,纵向采用低通滤波后的结果;右下的图像两个维度都采用高通滤波后的结果。
  在MATLAB中,采用函数dwt2()进行二维小波的单层分解，该函数的调用格式为:[cA, cH, cV, cD]=dwt2(X,‘wname’),该函数采用小波wname,对信号X进行单层分解。其中cA为近似系数,cH、CV和C加无小 节系数、垂直细节系数和对角细节系数.MATLAB中,采用函数idwt2()进行二维小波的单层重构,该函数的调用格式为:X=idwt2(cA,cH, cV, cD,‘wname’).
  在MATLAB中米用出双ae ec sy=wavedec2(X，N,‘wname’),该函数采用小波wanme对信号X进行二维小波的N层分解。利用函数waberec2()进行二维小波的多层重构，该函数的调用格式为:X=waverec2(C, s, ‘wname’)，利用小波wname进行二维小波的多层重构。
  在MATLAB中,采用函数wpdec()进行一维小波包分解该函数的调用格式为:T=wpdec(， N, ‘wname’):该函数对信号X进行N层的小波包分解,采用的小波为wname,返回值T为小波包树；T=wpdec(X，N, ‘wname’， E, P):该函数采用参数设置采用的熵，默认为’Shannon’.
  在MATLAB中,通过函数wpcoef()获取小波树上某个节点的小波包系数。
  在MATLAB中,采用函数wpsplt()将小波树上的节点进一步分解。
  在MATLAB中,采用函数wpjoin(()进行小波包树上的节点进行合并。
  在MATLAB中,采用函数besttree()获取最优小波树。
  在MATLAB中,通过函数wprec()进行一维小波包的重构,该函数的调用格式为:X=wprec(T)，其中T为小波包树，返回值X为重构的信号。
  在MATLAB中,采用函数wpdec2()进行二维小波包的分解,该函数的调用格式为:T=wpdec2(X，N, ‘wname’)该函数采用wname小波,对数据X进行二维N层小波包分解。同一维小波分解类似,采用函数wpcoef( )获取二维小波包树上某个节点的系数;采用函数wpsplt()进行二维小波包树的进一步分解;利用函数wpjoin()进行二维小波包树上节点的合并;利用函数besttree()获取最优的二维小波包树。通过函数wprec2()进行二维小波包的重构,该函数的调用格式为:X=wprec2(T)其中T为二维小波包树,X为重构后的二维数据。
  在MATLAB中,采用函数wenergy()计算进行归一化后的小波能量。该函数可以用于一维小波和小波包。该函数的调用格式为:[Ea, Ed]=wenergy(c, L):该函数用于计算一维小波的能量。=wenergy(T):该函数用于计算小波包的能量。在MATLAB中,采用函数wentropy()计算小波包的嫡。

3.GUI工具箱

  下面介绍小波工具箱的另一种实现方式,即GUI工具。小波工具箱的GUI工具界面友好，在解决特定问题时非常的直观和灵活,提供了大量的例子程序,而且可以非常方便的进行数据的导入和导出。用户不用编写程序，就采用小波分析对一维信号或二维图像进行压缩和去除噪声等。

edit wavemenu %%命令行运行指令

  在小波工具箱的GUI界面中,二维小波分析工具包括:二维小波分解（Wavelet 2-D)和二维小波包分解（(WaveletPacket 2-D)。下面介绍其中的二维小波分解。