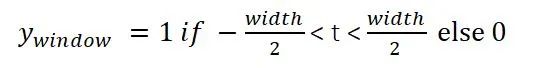图像变换—从傅里叶变换到小波变换

点击下方卡片，关注“人工智能与算法学习”公众号

重磅干货，第一时间送达

来源： 阿柴的算法学习日记

一、变换的本质

开门见山，变换的本质就是将原有的信号分解为最简单的表示。这个最简单的表示抽象出来就是基。基在向量空间中的表现就是一组两两无关的向量，向量空间中任一一个向量都可以用它们表示；在函数空间中的变现就是一组两两无关的函数，函数空间的任一一个函数都可以用它们表示。举一个很形象的例子，学计算机的人都知道计算机的任意文件在电脑中都是以0和1两个数字组成的，那么我们就可以把0、1称为文件空间的基。进一步，我们还得定义何为两两无关。在此，我们只看与我们息息相关的向量空间与函数空间。在向量空间与函数空间中的两两无关被定义为内积为0，也就是下图所示（上面为向量内积的定义，下面为函数内积的定义）：

有了这些基础，我们便可以开始去理解什么是傅里叶变换。

二、傅里叶变换（FT）

2.1、傅里叶级数

我们首先来看傅里叶级数，它是傅里叶变换的基础。傅里叶级数是法国数学家傅里叶发现的，他认为任何连续周期函数都可以由一组适当的正弦曲线组合而成。事实上从现在来看，这句话是错误的。它必须加上前提条件，也就是所谓的狄利克雷条件，但即便如此，这个发现在当时也是一个巨大的突破，它提供给人们一个全新视角来看待信号。由此，我们可以说：满足狄利克雷条件的周期信号，可以分解成一组适当的正余弦信号集。狄利克雷条件包括：

1）信号在一个周期内绝对可积

2）极值点个数有限

3）间断点个数有限

其实实际上大部分周期信号都满足狄利克雷条件，也就是说我们平常接触到的周期信号大多数都是可以进行傅里叶展开的。傅里叶级数实际上就是把这个空间中的一个向量通过基的线性组合的方式写出来。

我们已经知道了，两个正交的函数内积为 0 ，因此如果一个函数是由正交基的线性组合表示，我们可以很容易地求得它的系数。

设：

这就是傅里叶级数，实际上就是基的线性组合，1,.....,,......，就是这个函数空间的基。它们都是正交的也就是说它们两两内积为0。是 1 的系数，和分别是和的系数。现在我们想计算每一个基的系数。为此，我们试着计算一下它和其中一项的内积，比如

不过注意到不同的函数都是正交的，所以非零项只有.也就是说，。这么说似乎还是不明显，我这么写：

.

类比一下欧几里得空间。比如说二维欧式空间中，我取一组正交基，那么向量写成这组基的线性组合时系数分别是多少呢？答案就是

和.

实际上从空间的角度，二者确实没有什么本质区别。

那么现在我们已经理解了，傅里叶基其实就是这个函数构成的空间中的一组正交基，而傅里叶级数就是把空间里的元素写成基的线性组合。但我们注意到这里的函数是的，如果换一个区间，结果会如何呢？

2.2、傅里叶变换

我们把区间换成，这样相当于把每个函数“拉伸”了，这样每个基也拉伸了倍，变成了 或 ,.

而傅里叶级数就变成了

或

后面一种形式根据欧拉公式 由前一种形式简化而来

下面我们考虑指数函数形式的傅里叶级数在时的情形。

1）在区间变为后，傅里叶系数变为：

2）在的傅里叶展开中，把傅里叶系数带入，得到

3）上式的积分式是关于变量的，而外边的项与无关。因此可以写成

4）我们现在希望上式是黎曼和的形式，这样就可以写成定积分。为此取，这样上式变成

5）当时，，上式作为黎曼和的形式可以写成定积分:

6）上式略作变形，得到

这样，我们从傅里叶级数出发，在的情形下得到了一个式子。这个式子的本质仍然是一个求和式，只是因为极限所以写成了积分式。它把写成了的线性组合。等等！线性组合？！

确实如此啊。只是这里的变量是取遍整个数轴的。相当于对实数轴上的每个点都对应了这个函数的一个“基”，而这个积分式就是这些基的“线性组合”。

括号里的那堆东西，也就是

就叫做这个函数的傅里叶变换。

傅里叶变换是这样一个函数，它在处的函数值表示函数在对应的基上的系数。至此我们就完成了傅里叶变换从空间角度的介绍。

2.3、傅立叶变换的可视化理解

傅里叶变换的形式为： （此式与上一小节推导出的式子本质上相同，只是去掉了前面的系数，对后面的讨论没有影响），我们知道，根据欧拉公式，  。也就是说，傅里叶变换的本质就是：将原始信号乘上一组三角函数（正余弦），之后在整个时间域上积分。就这么简单！

你可能也听过，傅里叶变换是将函数从从时域转为频域。那么，为什么这么做就能将信号从时域转为频域呢？

我们来看一个信号：y = sin(3t)，如下图：

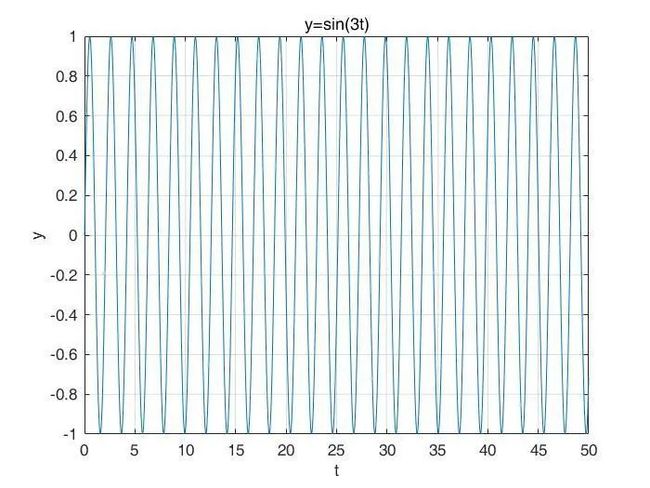
很好的周期性质，且每个周期的积分值都是0，是吧？如果对这个函数在  积分，那就是基本是0，因为  包含了无数个周期。PS：虽然这个积分在高数上不可积，但是你应该明白这里我要表达的意思：因为良好的周期性，且每个周期积分值是0，那么最后在很长的一段时间区间上积分，得到的还是一个很小的数，近似为0。

我们来用一段较长的时间区间计算一下，  ，符合我们的预计。

现在，我们来将这个信号乘上一个sin(4t) ，则信号变为y1 = sin(3t)*sin(4t)，如下图：

具有一个较短的小幅震动的周期和一个较长的主体周期，对吧？且每个主体周期的积分值都是0。同以上讨论，如果对这个函数在  积分，基本还接近于0，因为  包含了无数个主体周期。

我们来用一段较长的时间区间计算一下，  ，也比较符合我们的预计。

之后呢，我们来将这个信号乘上一个sin(3.1t) ，则信号变为y2 = sin(3t)*sin(3.1t)，如下图：

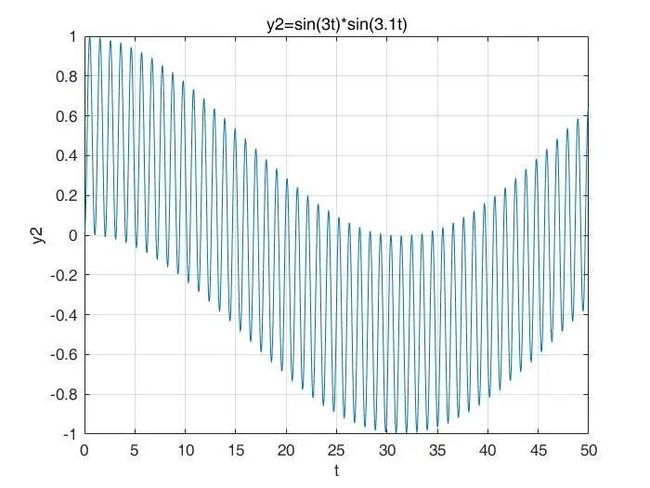
同样是有一个较短的小幅震动的周期和一个较长的主体周期，对吧？可以判断，每个主体周期的积分值都是0（虽然（0，50）这个区间没有完整地展示主题周期）。那么，依然同以上讨论，如果对这个函数在  积分，基本还接近于0，因为  包含了无数个主体周期。

我们来用之前的时间区间计算一下，  。

咦？这一次怎么距离0这么远了呢？

原因就是：对于sin(3t)*sin(4t)，它的主体周期较短，（0，50）是包含了好几个主体周期的，也就是说（0，50）在某种程度上是类似于  的。但是，对于sin(3t)*sin(3.1t)，它的主体周期很长，（0，50）连它的一个完整的主体周期都没有包含，那么（0，50）是不能类似于  的，积分值自然就比较大。

我们此时可以这样小小总结一下，对于信号y = sin(3t)，它的频率是3rad/s，（如果你喜欢用HZ，那就除以  ，就是  HZ，这里使用rad/s，是为了与前面的傅里叶变换的公式中的w一致），而sin(4t)的频率是4rad/s，sin(3.1t)的频率是3.1rad/s。如果在  积分，那么y1 = sin(3t)*sin(4t)，y2 = sin(3t)*sin(3.1t)的积分值都是0，也就是说，sin(4t)和sin(3.1t)在这里是没差别的。但是！！！如果在一个有限区间内积分，由于sin(3.1t)的频率3.1rad/s，距离原信号y = sin(3t)的频率3rad/s更近，那么sin(3.1t)和sin(3t)的乘积，也就是y2 = sin(3t)*sin(3.1t)的积分的绝对值会更大，也就是会离0更远。这里已经显示出一定的频率选择性了。

最后，让我们请出我们今天的主角，将这个信号乘上一个自己同频率的sin(3t) ，则信号变为y3 = sin(3t)*sin(3t)，如图：

Amazing！！！发现了什么？良好的周期性？还有呢？由于乘上了自己，任何时间的幅值都大于等于0了！不再满足周期内积分值为0这个条件了！那么，此时，我们对这个信号在  积分，就会得到一个非常非常大的数字。这个很大很大的数字就告诉你，这个信号和你乘的信号是同频率的！这就是可以知道信号中具有哪些频率部分了，不是吗？

我们还是来用之前的时间区间计算一下，  。是不是比其他的积分值都大了好多？

好了，我们已经知道，将一个信号乘上一个特定频率的sin函数，在  上积分，可以将信号中与sin函数同频率的部分筛选出来。那么，原则上讲，只要乘上所有频率的sin函数，并积分，不就知道原始信号中的所有频率部分了吗？

但是这样做需要把所有频率乘进去，做无数次计算哈！算不出来的。所以，我们将所乘的sin函数的频率作为符号变量w，来进行积分，即：

注意：这里的w只是一个符号，一个变量，这样的话，就只需要做一次积分，可以计算了。

计算出来X(w)之后，想知道特定的频率w0对应的积分值，直接将w0带入X(w)就立马得到积分值。也就知道原信号中是否含有这一频率的部分了。

好了，我们推导的这个式子，是不是与傅里叶变换的式子：

 

很像了呢？

这就是傅里叶变换的原理！乘上带有符号变量的sin、cos函数，并积分，就知道原始信号中的所有频率部分啦！

下面这幅图可以帮助我们更好的理解。

三、二维傅里叶变换-在图像上的应用

那首先来看一个例子~

其实右边图的每一个点，可以理解为它在描述一种平面波。

那…其实还是有两个点之间还是有半分钱关系的，右边点所描述的波是构成左边点的无数个波面中的其中一个。

右边图中，每一个点：

1）它到中点的距离描述的是频率

2）中点到它的方向，是平面波的方向

3）那一点的灰度值描述的是它的幅值

注：上述讲解来源见水印

四、傅里叶变换的局限性

我们现在来看两个信号，如下图：

  

这两个信号都是由sin(t)和sin(5t)组成的，y1是先出现了sin(5t)，再出现了sin(t)，y2是先出现了sin(t)，再出现了sin(5t)。

我们对它们进行FT，看看他们包含怎么样的频率，如下图：

y1,FT

y2,FT

Amazing！发现了什么？变换后的结果是一模一样的，都在w=1rad/s和w=5rad/s出现了峰值！这就可以说明FT的缺点了——FT只能提供频域信息，而完全丢失了时域信息！！！

不管某一频率的信号出现的时间是早还是晚，FT都是将它一视同仁地乘上sin和cos(FT的变换基函数)，然后在整个时间区间加和。因此，它不能提供某一频率信号出现的时间。

比如，对于上面两个信号，FT只能告诉我们，它们都有1rad/s和5rad/s的频率，而不能告诉我们1rad/s和5rad/s分别出现在哪个时间段。

所以，怎么办呢？？？

先别看下面，你自己想三想，你肯定可以想到的！

想一想——

想二想——

想三想——

好了，你想的是对的！

那就是把信号分成左右两半啊！左边进行一次FT，右边进行一次FT，很简单吧！好了，这就是短时傅里叶变换（STFT）的基本原理。

所以，接下来我们要正式开始步入—短时傅里叶变换（STFT），看看它是如何解决这个问题的。

五、短时傅里叶变换（STFT）

如上所述，我们将信号从中间截断，左边进行一次FT，右边进行一次FT，分别来看看。

y1左

y1右

y2左

y2右

可以看出，y1的左半部分是5rad/s，右半部分是1rad/s，y2恰好相反。这就说明，在y1中，(0, 25)的信号是5rad/s的频率，(25, 50)的信号是5rad/s的频率，y2恰好相反。这就是短时傅里叶变换的基本原理。

但是数学嘛，能用一个公式表达的，就别用一段话表达，截断、切开这些语句太不专业了。截断、切开的操作，更专业的讲叫作分窗，接下来我们来看一看。

首先，你可以想象一下，有一个窗子在这个信号上从左向右滑动，每次你都只能看到这个信号的一部分，所以我们把这个长度叫作窗长width。

现在我们来定义一个方窗函数： 

 ，如下图，即是width = 10 的一个方窗函数：

定义了方窗函数之后，我们只需要对方窗函数进行平移，再与原信号作乘，就相当于原来的截断、切开的操作，因此这种操作更专业地叫作分窗。

那么，将方窗函数向右平移了 （s可能是sliding的意思吧），再与原信号相乘，由于方窗函数除了中心的width部分是1外，其他部分都是0，这就相当于提取出了原信号在处，宽度为width的部分，这个信号分窗这个操作就可以写成：  。

如下两图所示，将  与  相乘，就相当于取出来了  中的(20,30)中的一段。

那么，我们对原信号中被提取出来的这一部分进行FT，就可以写成：

 

PS：这里之所以  要变成  ，是为了保证做FT的时候相乘的基函数具有统一性。

如此，变换后的代表原信号在处、宽度为width的部分的傅里叶变换，也就可以提取出来原信号在处、宽度为width的部分，包含各个频率部分的多少！带入不同的  ，也就是随着窗子的滑动，就可以知道不同的时间段内频率的成分。

我们采用width为10的方窗函数对

 进行STFT，如下：

首先，方窗函数位于  处，与原始信号相乘，选择出(0,10)的信号。

对选择出来的信号进行FT。可以看到，当时，选择的时间区间为(0,10)，这一部分只包含了  的频率成分。

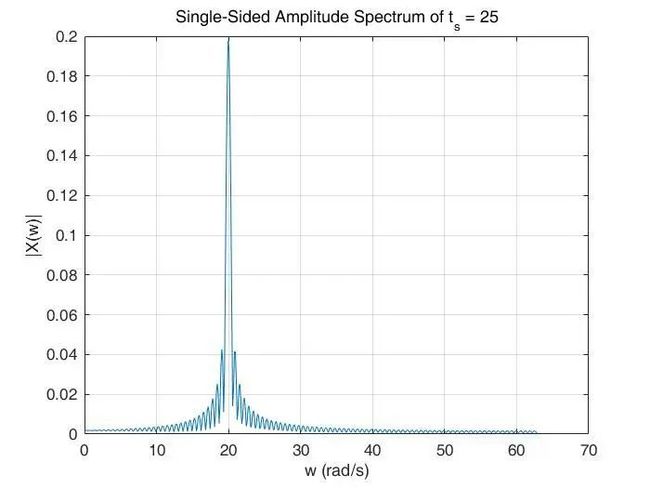
之后，方窗函数向右移动，与原始信号相乘，选择出不同时间区间的信号，进行FT。这里选择进行展示。

可以看到，当时，选择的时间区间为(20,30)，这一部分即包含了  的频率成分，也包含了  的频率成分。

重复以上过程，我们可以将方窗函数选择的不同时间区间的信号的FT的结果拼合起来，形成一张三维图。由此，我们即可知道，在  的时间区间内，信号具有怎么样的频率成分。

通过width = 10的方窗的STFT结果，我们可以知道，对于信号：

 

在(0,10)、(10,20)时间区间内，具有20rad/s的频率成分；在(20,30)时间区间内，具有1rad/s和20rad/s的频率成分；在(30,40)、(40,50)时间区间内，具有1rad/s的频率成分。

最后，进行三点重要的讨论。

第一点，变换之后的  是一个三维函数，它有两个自变量，  和w。 指的是原信号在处，w上一篇文章我们已经讨论过了，就是频率。所以，STFT提取出来的信息就是：原信号在处、宽度为width的部分，包含的频率信息。

原则上讲，可以得到任一对应的频率成分，如下图。

但是  是连续的，并不意味着你知道了每个时刻的频率成分，你知道的还只是 这一段区间内的频率信息。所以一般不需要计算所有的  ，每隔width计算一次即可。

你或许会想，我把width缩小一些，不就可以知道更精确的时间范围内的频率了吗？是的，你的猜想很对！但是，如此做也会带来一些频域分辨率的问题。这一点涉及到一些时域分辨率和频域分辨率的知识，我们下一篇文章会着重讲。

第二点，方窗函数是可以包含入变换基函数内部的，这组成了新的基函数，同时反映了STFT的本质。

我们来看， 如果定义

  

那么

那么，STFT的公式： 

 

就可以写成：

 

我们在上一篇文章里说过，变换就是将原信号乘上一个基函数，再积分的过程，那么，SDFT的基函数就是

  

Amazing！所以，STFT的本质是什么呢？

STFT的本质就是将FT的基函数  乘上一个方窗函数，形成了一个新的基函数 ！前面说的分窗、截断之类的都是表象，STFT的本质是基函数的改变！

那么，为什么STFT的基函数可以用于分窗，而FT的基函数不行呢？我们来看，我用正弦函数sin(5t)表示原来的基函数 ，那么FT基函数和STFT基函数如下：

原因就是：FT的基函数是在时域无限延伸的，因此，无论怎么平移，都是任分布在整个时域的，起不到分窗的作用。而STFT的基函数只在时域一段不为0，在剩下的时域都是0，因此，STFT的基函数的平移，就相当于自动加了窗子啦！

这种只在时域一段不为0，在剩下的时域都是0的性质被称为“紧支撑性”（compactly supported），具有这种性质的函数，平移之后与一个信号相乘，就相当于分窗操作。这一点很重要，我们之后讲小波变换的基函数的时候还会讲。

第三点，我们前面对于分窗操作使用的函数一直称为“方窗函数”，这是一种最理想的窗函数。还有一些其他的窗函数，比如，汉宁窗、海明窗、高斯窗等。窗函数本质都是一个窗子而已，原理是一模一样的，上面所有的讨论也都成立，只是这些窗子会让信号稍稍变形一丢丢而已。你就想像方窗函数就是一面平面镜，其他的窗函数就是哈哈镜就行了。

六、短时傅里叶变换（STFT）的缺点（为什么要提出小波变换）

3.1、分辨率问题

首先，我们需要了解一下海森堡测不准原理：  ，  为信号的时间不确定度，  为信号的频率不确定度。即，我们永远无法同时确定一个信号的确切时间和确切频率。

原因比较简单，频率其实就是时域周期性。如果我只给你一个数据点，问你这个数据点的频率是多少，这肯定是做不到的。要确定频率，就需要一个时域区间（包含几个时域周期）的信号。

时域区间越宽，信号的时间定位越不准，时间不确定度  越大，但是得到的频率越准，频率不确定度 越小；我们称之为：低的时域分辨率，高的频域分辨率。

时域区间越窄，信号的时间定位越准，时间不确定度  越小，但是得到的频率越不准，频率不确定度  越大；我们称之为：高的时域分辨率，低的频域分辨率。

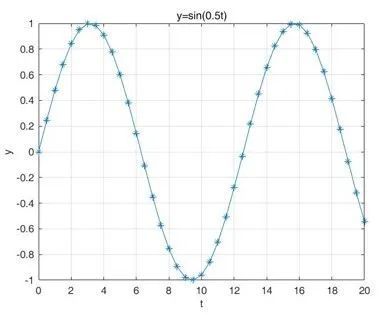
如上两图，对于第一个图中  的信号，要确定频率，即使把  都拿来，还是不太准，因为只包含了一个周期；对于第二个图中  的信号，要确定频率，取个  就差不多了，因为已经包含了好几个周期了。

我们来总结一下。

对于低频信号，为了更好地确定频率，我们希望，时域区间宽一些，即时间不确定度  大一些，根据海森堡测不准原理，频率不确定度 自然小一些；即低频信号，我们希望：宽窗子，低的时域分辨率，高的频域分辨率。

对于高频信号，为了更好地在时域定位，我们希望，时域区间窄一些，即时间不确定度  小一些，根据海森堡测不准原理，频率不确定度 自然大一些；即高频信号，我们希望：窄窗子，高的时域分辨率，低的频域分辨率。

上图所示是我们希望的动态分辨率。图中每个小矩形的  轴方向的宽度是时间区间大小，  轴方向的宽度是频率区间大小。注意，每个小矩形的面积是相等的，这保证了时域分辨率乘上频域分辨率是定值，最大程度满足海德堡测不准原理。通过图可以看出，我们希望，对于低频信号：低的时域分辨率，高的频域分辨率；对于高频信号：高的时域分辨率，低的频域分辨率。

对于整体低频、局部高频的信号，这种动态调整分辨率的规则特别有用。在实际信号中，频率非常高的高频信号往往是一种噪声，只在局部出现，基本都满足整体低频、局部高频这一条件。

最后，我们再来看两张分辨率图来强化一下对于分辨率的理解。

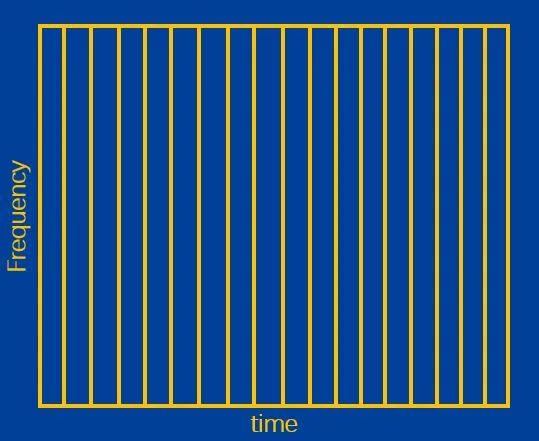
上图是一张采集信号的分辨率图。每个小矩形的  轴方向的宽度是很小，  轴方向的宽度很大。也就是说，其时域分辨率很好，可以确切地确定每个信号采样点的时间，但是其频域分辨率很差，或者说完全不具有频域分辨率。

上图是一张傅里叶变换（FT）的分辨率图。每个小矩形的  轴方向的宽度是很大，  轴方向的宽度很小。也就是说，其频域分辨率很好，可以比较精确地确定信号中的频率成分，但是其时域分辨率很差，或者说完全丢失了时域分辨率。

傅里叶变换的这一特性，这一点我在上一篇文章里讲过，这也是我们转而使用短时傅里叶变换（STFT）的原因。

3.2、短时傅里叶变换（STFT）的缺点

我们来回忆一下STFT，STFT的窗长是固定的，即时域分辨率是固定的，根据海德堡测不准原理，其频域分辨率也是固定的。其分辨率图如下：

每个小矩形的  轴方向的宽度和 轴方向的宽度是恒定的！也就是说，不论高频低频，其时域和频域分辨率都不可调，这与我们之前讨论的“对于低频信号：低的时域分辨率，高的频域分辨率；对于高频信号：高的时域分辨率，低的频域分辨率”这一原则不符合。

这种不符合会带来什么后果呢？

如图所示正弦信号，0~250ms：300HZ，250~500ms：200HZ ，500~750ms：100HZ ， 750~1000ms：50HZ。

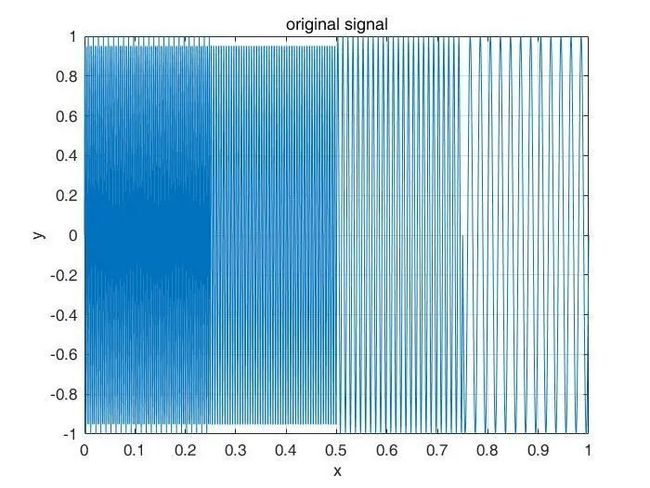
选择一个较窄的窗子 做STFT，结果如下：

当窗子较窄的时候，STFT的时域分辨率还行，但是频域分辨率不佳。

我们选择一个宽一些的窗子  做STFT，结果如下：

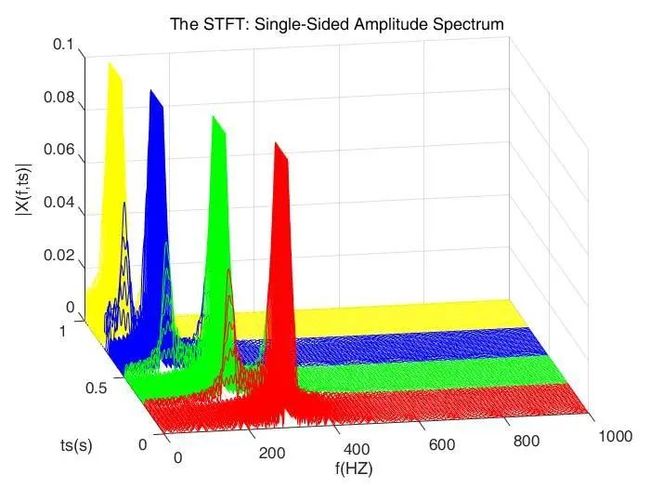
当窗子较宽的时候，STFT的频域分辨率很好，基本可以确定频率，但是时间轴上开始出现交叠了，也就是时域分辨率下降了。

我们选择一个更宽的窗子  做STFT，结果如下：

当窗子更宽的时候，STFT的频域分辨率非常好了，但是时域分辨率已经很差了，时间轴上出现了大规模的交叠现象。

我们来总结一下，对于STFT，如果窗子的宽度选择合适，是可以得到时域和频域分辨率都“还可以”的结果的（由于STFT的分辨率固定，只能说“还可以”，不能说“满意”，因为我们最想要的是动态分辨率）。但是，在变换之前，我们也不知道选择多宽的窗子是合适的。

这就是STFT的缺点：

1、时间和频率分辨率都固定，不能随着频率的高低实现动态可调；

2、选择一个合适的窗宽十分困难。

这也正是小波变换提出的动机。

相关资料：

[1] https://zhuanlan.zhihu.com/p/66246381

[2] https://zhuanlan.zhihu.com/p/68323379

本文仅做学术分享，如有侵权，请联系删文。

—THE END—

分享

收藏

点赞

在看