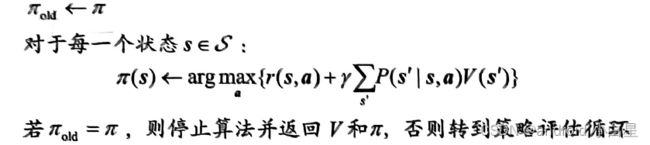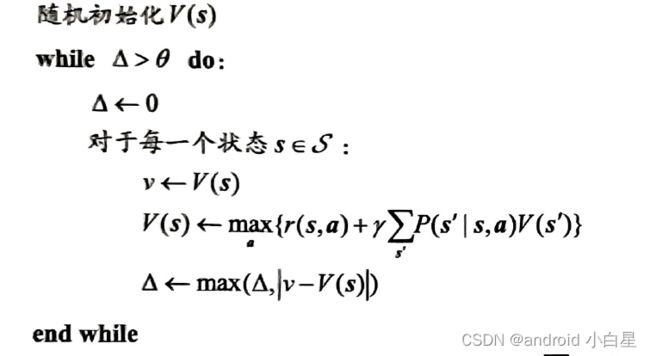强化学习之蒙特卡罗（MC）、动态规划（DP）、时间差分（TD）

1.马尔可夫决策过程(MDP)

1.马尔可夫性质

当且仅当某时候的状态只取决于上一时刻的状态时，一个随机过程被称为具有马尔可夫性质。
$$P(S_{t+1}|S_t)=P(S_{t+1}|S_1,...,S_t)$$

---

2.马尔可夫过程

指具有马尔可夫性质的随机过程被称为马尔可夫过程，通常用元组描述。

S表示有限数量的状态集合，终止状态是指它不会再转移到其他状态。
$$S=\{s_1,s_2,...s_n\}$$
P是状态转移矩阵，定义所有状态对之间的转移概率，某个状态到其他状态的概率和必须为1。
P = [ P ( s 1 ∣ s 1 ) . . . P ( s n ∣ s 1 ) . . . . . . . . . P ( s 1 ∣ s n ) . . . P ( s n ∣ s n ) ] P=\begin{bmatrix} P(s_1|s_1) & ...& P(s_n|s_1) \\ ... & ... &...\\P(s_1|s_n)&...&P(s_n|s_n) \end{bmatrix} P= ​P(s1​∣s1​)...P(s1​∣sn​)​.........​P(sn​∣s1​)...P(sn​∣sn​)​ ​

3.马尔可夫奖励过程(MRP)

再马尔可夫过程的基础上加入奖励函数r和折扣因子γ，就可以得到马尔可夫奖励过程，通常由构成。

S是有限状态的集合。

P是状态转移矩阵。

r是奖励函数，某个状态s的奖励r(s)指转移到该状态时可以获得的奖励的期望。

γ是折扣因子，取值范围为[0,1)。

(1) 回报：

在马尔可夫奖励过程中，从第t时刻状态St开始，直到终止状态时，所有奖励的衰减之和称为回报。
$$G_t=R_t+\gamma R_{t+1}+r^2{R}_{t+2}+...=\sum _{i=0}^{\infty }{r}^k{R}_{t+k}$$
(2) 价值函数：

在马尔可夫奖励过程中，一个状态的期望回报被称为这个状态的价值。价值函数输入为某个状态，输出为这个状态的价值。
$$\begin{gathered} V(s)=E[G_t|S_t=s] \\ V(s)=r(s)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V(s^{\prime }) \end{gathered}$$
(3)贝尔曼方程:
$$\begin{gathered} V=R+\gamma PV \\ (I-rP)V=R \\ V=(I-rP{)}^{-1}R \end{gathered}$$
贝尔曼方程的计算复杂度O(n3)，求解较大规模的马尔可夫奖励过程的价值函数时，可以使用动作规划(DP)算法，蒙特卡洛方法(MC)和时序差分(TD)。

4.马尔可夫决策过程(MDP)

​ 马尔可夫过程和马尔可夫奖励过程都是自发改变的随机过程，在这基础上加一个外界的“刺激”（智能体的动作）来改变这个随机过程，就有了马尔可夫决策过程，通常由。

S是状态的集合。

A是动作的集合。

γ是折扣因子。

r(s,a)是奖励函数，此时奖励可能同时取决于状态s和动作a。

P(s’|s,a)是状态转移函数，表示在状态s执行动作a之后到达状态s‘的概率。

r’(s)表示在一个MRP状态s的奖励。
$$r^{\prime }(s)=\sum _{a\in A}\pi (a|s)r(s,a)$$
P’(s’|s)表示在一个MRP的状态从s转移至s’的概率。
$$P^{\prime }(s^{\prime }|s)=\sum _{a\in A}\pi (a|s)P(s^{\prime }|s,a)$$
(1)策略：

策略Π(a|s)表示输入状态为s的情况下采取动作a的概率。
$$\pi (a|s)=P(A_t=a|S_t=s)$$
(2)状态价值函数:

从状态s出发遵循策略Π能获得的期望回报，被称为状态价值函数VΠ(s)。
$$V^{\pi }(s)=E_{\pi }[G_t|S_t=s]$$
(3)动作价值函数:

从状态s出发，遵循策略Π并执行动作a得到的期望回报，被称为动作价值函数QΠ(s,a)。
$$Q^{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$$
状态s的价值等于在该状态下基于策略Π采取所有动作的概率和相应的价值相乘再求和的结果。
$$V^{\pi }(s)=\sum _{a\in A}\pi (a|s)Q^{\pi }(s,a)$$
状态s下采取动作a的价值等于即时奖励加上经过衰减的所有可能的下一个状态的状态转移概率和相应的价值乘积。
$$Q^{\pi }(s,a)=r(s,a)+r\sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })$$
(4)贝尔曼期望方程:

由上式推导可得
$$\begin{gathered} Q^{\pi }=r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime }|a^{\prime }) \\ {V}^{\pi }(s)=\sum _{a\in A}\pi (a|s)(r(s,a)+r\sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })) \end{gathered}$$
(5)贝尔曼最优方程：

强化学习的目标：通常是找到一个策略，使得智能体从初始状态出能获得最多的期望回报。

*最优策略(Π(s))：**在有限状态和动作集合的MDP中，至少存在一个策略比其他所有策略都好或者至少存在一个策略不差于其他所有策略。

最优状态价值函数：
$$V^{\ast }(s)=\underset{\pi }{\max }{V}^{\pi }(s)$$
最优动作价值函数：
$$Q^{\ast }(s,a)=\underset{\pi }{\max }{Q}^{\pi }(s,a)$$
为了使用最优动作价值函数最大，需要在当前状态动作对(s,a)之后都执行最优策略。
$$\begin{gathered} Q^{\ast }(s,a)=r(s,a)+r\sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\ast }(s^{\prime }) \\ {V}^{\ast }(s^{\prime })=\underset{a\in A}{\max }{Q}^{\ast }(s,a) \end{gathered}$$
根据最优状态价值函数和最优动作价值函数的关系，以及贝尔曼方程，得到贝尔曼最优方程。
$$\begin{gathered} V^{\ast }(s)=\underset{a\in A}{\max }\{r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\ast }(s^{\prime })\} \\ {Q}^{\ast }(s,a)=r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)\underset{a^{\prime }\in A}{\max }{Q}^{\ast }(s^{\prime },a^{\prime }) \end{gathered}$$
V*(s)与VΠ(s)的区别：前者会按照获取最多期望回报的动作来取值，其他动作则不会赋予概率，类似于贪心算法；后者会根据策略Π对各个动作的概率分配获取的期望回报来求和， 就是求期望。

2.蒙特卡罗（MC）、动态规划（DP）、时间差分（TD）

这些方法用于找到一个策略，使得智能体从初始状态出能获得最多的期望回报。

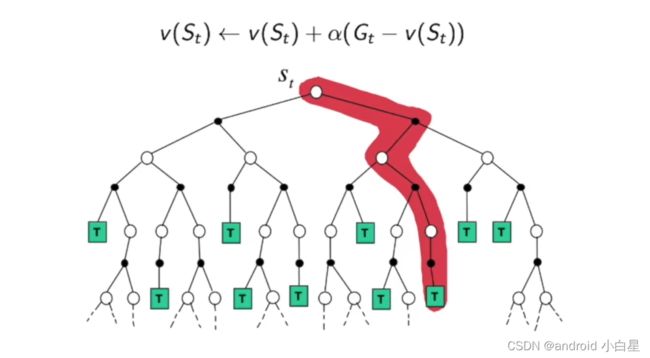
1.蒙特卡罗(MC)

如图所示，蒙特卡罗需要一个完整的路径。

蒙特卡罗公式的推导：

(1).状态价值的期望回报：当策略在MDP上采样很多条序列，计算从这个状态出发的回报再求其期望。
$$V^{\pi }=E_{\pi }[G_t|S_t=s]\approx \frac{1}{N}\sum _{i=1}^N{G}_t^{(i)}$$
(2).采用增量式更新来推导。
$$\begin{gathered} V_N^{\pi }=\frac{1}{N}\sum _{i=1}^N{G}_t^{(i)} \\ =\frac{1}{N}(G_t+\sum _{i=1}^{N-1}{G}_t^{(i)}) \\ =\frac{1}{N}(G_t+(N-1)V_{N-1}^{\pi }(s)) \\ =V_{N-1}^{\pi }(s)+\frac{1}{N}(G_t-V_{N-1}^{\pi }(s)) \\ (V_{N-1}^{\pi }(s)表示V_N^{\pi }的前一步的值，都是表示同一状态) \end{gathered}$$
(3).蒙特卡罗公式。
$$\begin{gathered} 1.收集episode(S_1,A_1,R_1,....S_t) \\ 2.状态S_t的回报为G_t \\ N(S_t)\leftarrow N(S_t)+1 \\ V(S_t)\leftarrow V(S_t)+\frac{1}{N(S_t)}(G_t-V(S_t)) \end{gathered}$$

2.动态规划(DP)

动态规划：将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到目标问题的解。

基于动态规划的强化学习分为策略迭代(policy iteration)和价值迭代(value iteration)。

(1).策略迭代

策略迭代由两部分组成：策略评估(policy evaluation)和策略提升(policy improvement)。

i.策略评估：根据之前学习的贝尔曼期望方程，可以得到，当知道奖励函数r(s,a)和状态转移函数p(s’|s,a)时，可以根据下一个状态的价值来计算当前状态的价值。因此，可以把下一个可能状态的价值当成一个子问题，把当前状态的价值看作成当前问题。公式如下：
$$V^{k+1}(s)=\sum _{a\in A}\pi (a|s)(r(s,a)+r\sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^k(s^{\prime }))$$
当子问题和当前问题之间的差值比较小时，则证明迭代已经收敛，可以结束策略评估。

ii.策略提升:可以贪心地在每一个状态选择动作价值最大的动作。
$${\pi }^{\prime }(s)=arg\underset{a}{\max }{Q}^{\pi }(s,a)=arg\underset{a}{\max }\{r(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })\}$$
策略迭代算法：

(2).价值迭代

价值迭代直接由贝尔曼最优方程来进行动态规划 ，得到最终的最优状态价值函数。

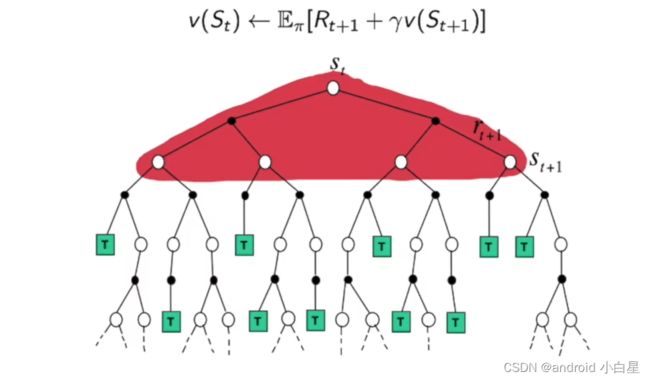
3.时间差分(TD)

时序差分：用来估计一个策略的价值函数的方法，它结合了蒙特卡罗和动态规划算法的思想。

1. 时序差分方法和蒙特卡罗的相似之处在于可以从样本数据中学习，不需要事先知道环境(由他们公式可知，不需要知道P(s’|s,a)）；
2. 和动态规划的相似之处在于可以根据贝尔曼方程的思想，利用后续状态的价值估计来更新当前状态的价值估计。

时序差分(TD)：
$$r_t+\gamma V(s_{t+1})-V(s_t)$$

4. MC、DP、TD之间的关系。

右下角表示穷举法。

MC与TD的区别：

1. TD可以在每一步后在线学习。
   MC 必须等到episode结束才能知道return。
2. TD 可以从不完整的序列中学习。
   MC 只能从完整序列中学习。
3. TD 在连续（非终止）环境中工作。
   MC 仅适用于 episodic（终止）环境。
4. TD利用马尔可夫特性，在马尔可夫环境中更高效。
   MC 不利用马尔可夫特性，在非马尔可夫环境中更有效。

待续。。。强化学习TD的相关算法。

参考资料：
周博磊强化学习课程
张伟楠等动手学深度学习
强化学习相关代码：https://github.com/boyu-ai/Hands-on-RL