LeetCode算法小抄--二叉树的各种遍历
LeetCode算法小抄--二叉树的各种遍历
- 二叉树
-
-
- 树的深度
-
- [104. 二叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-binary-tree/)
- 前序遍历
-
- [543. 二叉树的直径](https://leetcode.cn/problems/diameter-of-binary-tree/)
- 层序遍历
-
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计5522字,阅读大概需要3分钟
更多学习内容, 欢迎关注【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
二叉树
二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
两个经典排序算法 快速排序 和 归并排序,对于它俩,你有什么理解?
快速排序就是个二叉树的前序遍历,归并排序就是个二叉树的后序遍历。
快速排序的逻辑是,若要对 nums[lo..hi] 进行排序,我们先找一个分界点 p,通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p],且 nums[p+1..hi] 都大于 nums[p],然后递归地去 nums[lo..p-1] 和 nums[p+1..hi] 中寻找新的分界点,最后整个数组就被排序了。
void sort(int[] nums, int lo, int hi) {
/****** 前序遍历位置 ******/
// 通过交换元素构建分界点 p
int p = partition(nums, lo, hi);
/************************/
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}
归并排序的逻辑,若要对 nums[lo..hi] 进行排序,我们先对 nums[lo..mid] 排序,再对 nums[mid+1..hi] 排序,最后把这两个有序的子数组合并,整个数组就排好序了。
// 定义:排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
int mid = (lo + hi) / 2;
// 排序 nums[lo..mid]
sort(nums, lo, mid);
// 排序 nums[mid+1..hi]
sort(nums, mid + 1, hi);
/****** 后序位置 ******/
// 合并 nums[lo..mid] 和 nums[mid+1..hi]
merge(nums, lo, mid, hi);
/*********************/
}
树的深度
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
思路一:遍历一遍二叉树,用一个外部变量记录每个节点所在的深度,取最大值就可以得到最大深度,这就是遍历二叉树计算答案的思路。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
// 遍历二叉树的思路
class Solution {
// 记录最大深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;
public int maxDepth(TreeNode root) {
traverse(root);
return res;
}
private void traverse(TreeNode root){
if(root == null) return;
// 前序位置
depth++;
if(root.left == null && root.right == null){
// 到达叶子节点,更新最大深度
res = Math.max(res, depth);
}
traverse(root.left);
traverse(root.right);
// 后序位置
depth--;
}
}
1、为什么需要在前序位置增加 depth,在后序位置减小 depth?
因为前面说了,前序位置是进入一个节点的时候,后序位置是离开一个节点的时候,depth 记录当前递归到的节点深度,你把 traverse 理解成在二叉树上游走的一个指针,所以当然要这样维护。
2、对 res 的更新,放到前中后序位置都可以,只要保证在进入节点之后,离开节点之前(即 depth 自增之后,自减之前)就行了。
思路二:一棵二叉树的最大深度可以通过子树的最大深度推导出来,这就是分解问题计算答案的思路。
// 分解二叉树的思路
class Solution {
// 定义:输入根节点,返回这棵二叉树的最大深度
public int maxDepth(TreeNode root) {
if(root == null) return 0;
// 利用定义,计算左右子树的最大深度
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// 整棵树的最大深度等于左右子树的最大深度取最大值,
// 然后再加上根节点自己
int res = Math.max(leftMax, rightMax) + 1;
return res;
}
}
前序遍历
// 遍历二叉树的思路
List<Integer> res = new LinkedList<>();
// 返回前序遍历结果
List<Integer> preorderTraverse(TreeNode root) {
traverse(root);
return res;
}
// 二叉树遍历函数
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
res.add(root.val);
traverse(root.left);
traverse(root.right);
}
是否能够用「分解问题」的思路,来计算前序遍历的结果?
换句话说,不要用像 traverse 这样的辅助函数和任何外部变量,单纯用题目给的 preorderTraverse 函数递归解题,会不会?
思路:一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果。
// 定义:输入一棵二叉树的根节点,返回这棵树的前序遍历结果
List<Integer> preorderTraverse(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
// 前序遍历的结果,root.val 在第一个
res.add(root.val);
// 利用函数定义,后面接着左子树的前序遍历结果
res.addAll(preorderTraverse(root.left));
// 利用函数定义,最后接着右子树的前序遍历结果
res.addAll(preorderTraverse(root.right));
return res;
}
中序和后序遍历也是类似的,只要把 add(root.val) 放到中序和后序对应的位置就行了
这个解法短小精干,但为什么不常见呢?
一个原因是这个算法的复杂度不好把控,比较依赖语言特性。
Java 的话无论 ArrayList 还是 LinkedList,addAll 方法的复杂度都是 O(N),所以总体的最坏时间复杂度会达到 O(N^2),除非你自己实现一个复杂度为 O(1) 的 addAll 方法,底层用链表的话是可以做到的,因为多条链表只要简单的指针操作就能连接起来。
1、如果把根节点看做第 1 层,如何打印出每一个节点所在的层数?
// 二叉树遍历函数
void traverse(TreeNode root, int level) {
if (root == null) {
return;
}
// 前序位置
printf("节点 %s 在第 %d 层", root, level);
traverse(root.left, level + 1);
traverse(root.right, level + 1);
}
// 这样调用
traverse(root, 1);
2、如何打印出每个节点的左右子树各有多少节点?
// 定义:输入一棵二叉树,返回这棵二叉树的节点总数
int count(TreeNode root) {
if (root == null) {
return 0;
}
int leftCount = count(root.left);
int rightCount = count(root.right);
// 后序位置
printf("节点 %s 的左子树有 %d 个节点,右子树有 %d 个节点",
root, leftCount, rightCount);
return leftCount + rightCount + 1;
}
543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
关键在于,每一条二叉树的「直径」长度,就是一个节点的左右子树的最大深度之和。
现在让求整棵树中的最长「直径」,那直截了当的思路就是遍历整棵树中的每个节点,然后通过每个节点的左右子树的最大深度算出每个节点的「直径」,最后把所有「直径」求个最大值即可。
class Solution {
// 记录最大直径的长度
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
// 对每个节点计算直径,求最大直径
traverse(root);
return maxDiameter;
}
// 遍历二叉树
private void traverse(TreeNode root){
if(root == null) return;
// 对每个节点计算直径
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
int myDiameter = leftMax + rightMax;
// 更新全局最大直径
maxDiameter = Math.max(maxDiameter, myDiameter);
traverse(root.left);
traverse(root.right);
}
// 计算二叉树的最大深度
private int maxDepth(TreeNode root){
if(root == null) return 0;
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
return Math.max(leftMax, rightMax) + 1;
}
}
解法是正确的,但是运行时间很长,原因也很明显,traverse 遍历每个节点的时候还会调用递归函数 maxDepth,而 maxDepth 是要遍历子树的所有节点的,所以最坏时间复杂度是 O(N^2)。
由于前序位置无法获取子树信息,所以只能让每个节点调用 maxDepth 函数去算子树的深度。那如何优化?我们应该把计算「直径」的逻辑放在后序位置,准确说应该是放在 maxDepth 的后序位置,因为 maxDepth 的后序位置是知道左右子树的最大深度的。
class Solution {
// 记录最大直径的长度
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
maxDepth(root);
return maxDiameter;
}
// 计算二叉树的最大深度
private int maxDepth(TreeNode root){
if(root == null) return 0;
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// 后序位置,顺便计算最大直径
int myDiameter = leftMax + rightMax;
// 更新全局最大直径
maxDiameter = Math.max(maxDiameter, myDiameter);
return Math.max(leftMax, rightMax) + 1;
}
}
层序遍历
二叉树题型主要是用来培养递归思维的,而层序遍历属于迭代遍历,比较简单
// 输入一棵二叉树的根节点,层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
if (root == null) return;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// 从上到下遍历二叉树的每一层
while (!q.isEmpty()) {
int sz = q.size();
// 从左到右遍历每一层的每个节点
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 将下一层节点放入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
}
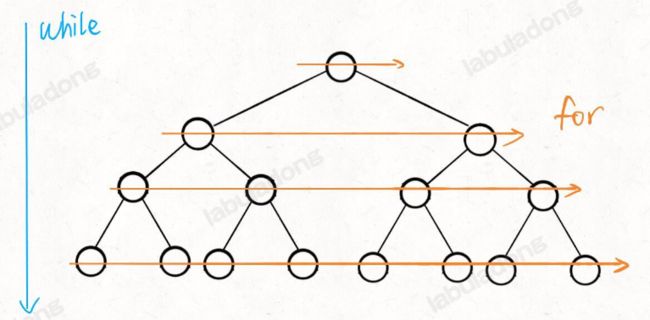
这里面 while 循环和 for 循环分管从上到下和从左到右的遍历
–end–