数据结构_第十一关:二叉树的链式结构
目录
1.二叉树链式结构的实现
1.1前置说明
1.2二叉树的遍历
1.3二叉树遍历的实现:
1)先序遍历、中序遍历、后续遍历代码如下
2)层序遍历:
1.4结点个数以及高度的计算
1)求二叉树的总节点:
2)求叶子节点的个数
3)求树的深度/高度
4)求第K层的结点数 k>=1
5)二叉树查找值未x的节点
2.二叉树的基础OJ题练习
1.二叉树链式结构的实现
1.1前置说明
此次二叉树链式结构的讲解先不进行增删查改,之后学完c++再进一步学习
事实上,二叉树的增删查改没有价值,
学习二叉树的意义是:再其基础上完成对搜索二叉树的学习
搜索二叉树:左孩子比父节点小,右孩子比父节点大
搜索二叉树学习完之后,就到了对平衡二叉树(AVL树+红黑树)的学习,
这里就不多介绍了(绝不是因为我现在也不太懂^.^)
1.2二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础
四种遍历方法:
- 先序遍历:根、左子树、右子树
- 中序遍历:左子树、跟、右子树
- 后序遍历:左子树、右子树、跟
- 层序遍历:从第一层开始、每层从左到右,一层一层的走
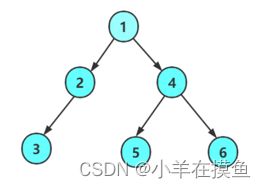
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
层次遍历结果:1 2 4 3 5 6
练习:请写出下面的前序/中序/后序/层序遍历
选择题:
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。
该完全二叉树的前序序列为( )
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为( )
A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
答案:1.A 2.A 3.D 4.A
1.3二叉树遍历的实现:
在实现前,我们先要建立一个树,因为我们暂时不学习二叉树的建立,
所以我们直接手动建立如下图的二叉树
手动建立如下:
#include
#include
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
int main()
{
BTNode* root;
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
return 0;
} 1)先序遍历、中序遍历、后续遍历代码如下
因为他们的代码只是遍历顺序不同,所以就放一起了
//前序遍历
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
//printf("NULL ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
//printf("NULL ");
return;
}
PrevOrder(root->left);
printf("%d ", root->data);
PrevOrder(root->right);
}
//后续遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
//printf("NULL ");
return;
}
PrevOrder(root->left);
PrevOrder(root->right);
printf("%d ", root->data);
}2)层序遍历:
-
首先,将二叉树的根节点放入一个队列中。
-
从队列的头部取出一个元素(记为当前元素cur),将cur的左孩子作为新节点放入队列尾部,再将cur的右孩子作为新节点放入队列尾部。因为队列是先进先出的,所以这样处理后,下一次取出来的就是左孩子,再下一次取出来的就是右孩子了。
-
重复步骤2,直到队列为空为止。
void LevelOrder(BTNode* root)
{
if (root == NULL)
return;
BTNode* queue[1000]; // 定义队列,最多存放1000个节点
int head = 0, tail = 0;
queue[tail++] = root;
while (head < tail)
{
BTNode* curNode = queue[head++]; // 出队
printf("%d ", curNode->data);
if (curNode->left != NULL)
queue[tail++] = curNode->left; // 左孩子入队
if (curNode->right != NULL)
queue[tail++] = curNode->right; // 右孩子入队
}
}1.4结点个数以及高度的计算
因为二叉树适合用递归的方式来计算,所以不论是上面的遍历二叉树还是其他计算,他们的代码都是用递归来实现的
1)求二叉树的总节点:
有两种方法:
- 定义一个全局变量size,在每次计算前都要手动将其置为0
- 直接用递归来进行计算
方法1:
int size = 0;//定义全局变量
void TreeSize1(BTNode* root)
{
if (root == NULL)
return;
size++;
TreeSize1(root->left);
TreeSize1(root->right);
}
//使用时:
int main()
{
size = 0; //size是全局变量,每次使用前都需要手动置0,否则会在之前的基础上再加
TreeSize1(n1);
printf("TreeSize1:%d\n", size);
TreeSize1(n1);
printf("TreeSize1(size未置0):%d\n", size);
size = 0;
TreeSize1(n1);
printf("TreeSize1(重新将size置0):%d\n", size);
return 0;
}结果如下:
方法二:直接用递归来求:
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right) + 1;
}
//使用
int main()
{
printf("TreeSize2:%d\n", TreeSize2(n1));
printf("TreeSize2:%d\n", TreeSize2(n1));
printf("TreeSize2:%d\n", TreeSize2(n1));
return 0;
}2)求叶子节点的个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}3)求树的深度/高度
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
//保留算出的数据,防止重复计算比较
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}注意这里写的时候不要像下面那样直接返回,
return TreeLeafSize(root->left) > TreeLeafSize(root->right) ?
TreeLeafSize(root->left) + 1 : TreeLeafSize(root->right) + 1;这种写法十分浪费资源,会有很多重复的计算,导致效率特别低
正确的写法是先将其保存起来,再进行比较和返回递归
4)求第K层的结点数 k>=1
int TreeKLevelSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
// k > 1 子树的k-1
return TreeKLevelSize(root->left, k - 1)+ TreeKLevelSize(root->right, k - 1);
}5)二叉树查找值未x的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
BTNode* ret2 = TreeFind(root->right, x);
if (ret2)
return ret2;
}2.二叉树的基础OJ题练习
(思路和代码下一关里面讲)
- 1. 单值二叉树。 OJ题链接
- 2. 检查两颗树是否相同 OJ题链接
- 3. 对称二叉树。 OJ题链接
- 4. 另一颗树的子树。 OJ题链接