Level3题目整理
文章目录
-
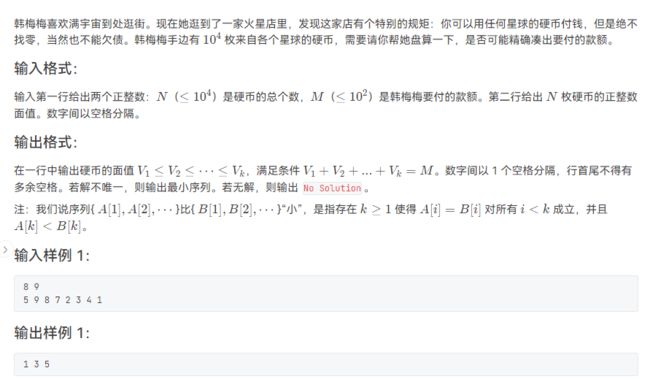
- L3-001 凑零钱
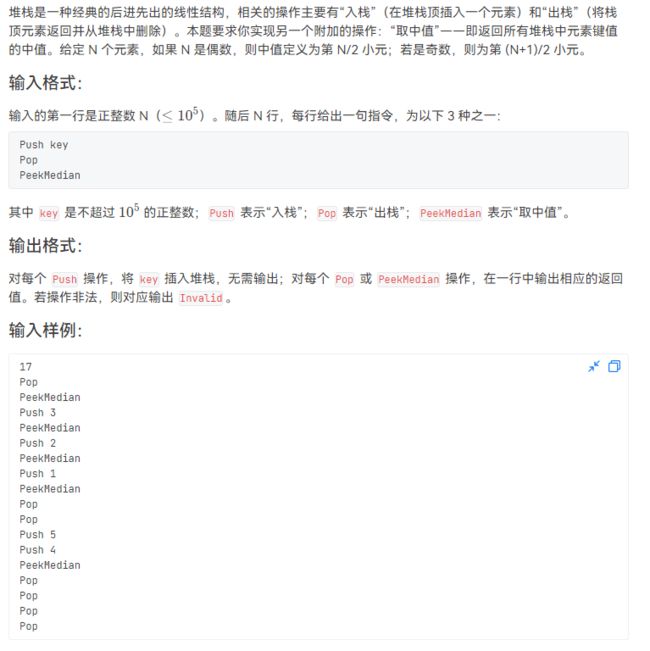
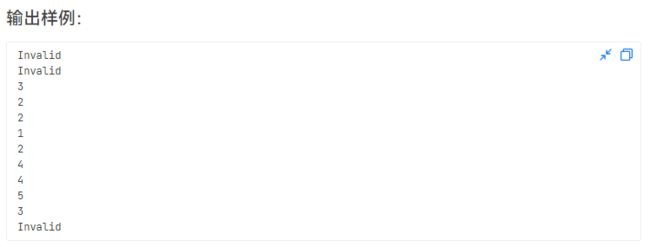
- L3-002 特殊堆栈
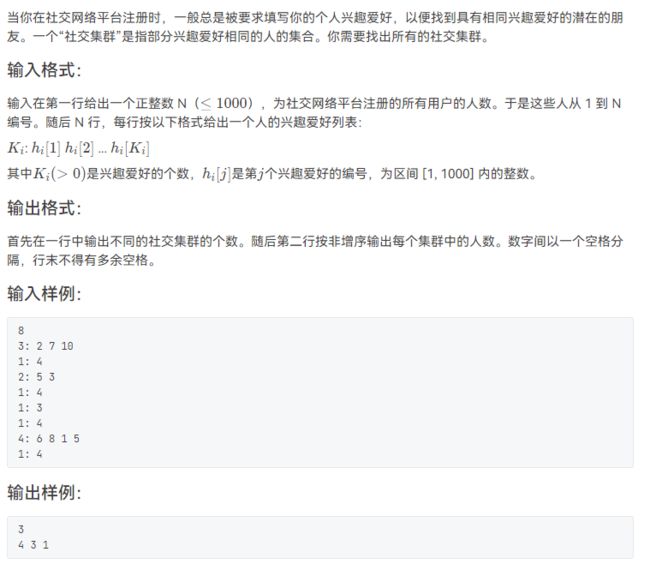
- L3-003 社交集群(并查集+vector+暴力⭐)
- L3-004 肿瘤诊断(三维bfs)
- L3-005 垃圾箱分布(多次dijkstra)
- L3-008 喊山(邻接表+bfs)
- L3-010 是否完全二叉搜索树(不用建树判断是否满足,并输出层序遍历序列⭐⭐⭐)
L3-001 凑零钱
#include暴力解法:()
也可以过很多,先排个序,优先全选最小的,所以只要存在第一种方案即是最优的
#includeL3-002 特殊堆栈
需要注意在peekMedian时,进行排序时,我们不能对进行模拟的数组直接进行排序,这样排序后会影响后续操作,我们应该再开一个辅助数组进行进行排序和输出。
#include法二:采用vector顺序插入,lower_bound(),
#includeL3-003 社交集群(并查集+vector+暴力⭐)
对于每个有相同爱好的人我们进行merge,并维护每一个集合的大小,对于判断两个人是否有相同爱好,我们暴力就可以过,最后对于每个集合,将集合大小存入multiset,进行从大到小排序即可
#includeL3-004 肿瘤诊断(三维bfs)
#include法2:三维bfs
#includeL3-005 垃圾箱分布(多次dijkstra)
思路:以垃圾桶为源点分别进行dijkstra,存下来可行的答案,排序输出即可
需要处理:因为垃圾桶为G1-Gm所以我们将垃圾桶映射到n+1到n+m即可
(1)需要注意每次选取的最小值应该是!vis[i]
(2)每次都需要进行初始化
坐标映射:
int isP(string x) {
int index;
if(x[0] == 'G') {
index = n + stoi(x.substr(1));
} else {
index = stoi(x);
}
return index;
}
#includeL3-008 喊山(邻接表+bfs)
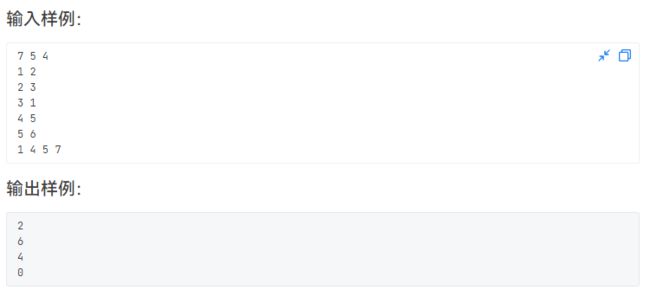
刚开始想着用dfs,发现有两个点过不了,
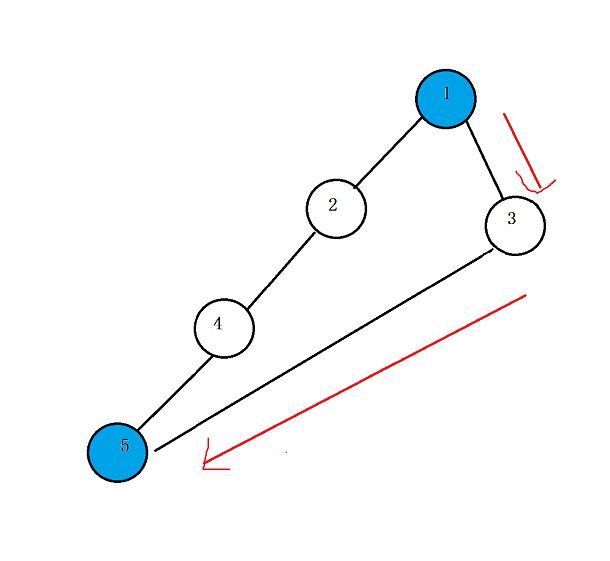
由上图可以直到,dfs是深度优先,我们会觉得5是最远的,其实4和5是一样远的,但是答案要输出编号更小的,所以正确答案为4,很明显本题能看出来传递是一层一层的,所以这种问题用bfs更好,第一次找到某点一定是路径最短的,所以我们采用bfs进行查找,需要注意每次标记,特别是标记起始那个点,要不会死循环。
#includeL3-010 是否完全二叉搜索树(不用建树判断是否满足,并输出层序遍历序列⭐⭐⭐)
首先根据规则建树,并且在建树的过程中,我们就可以直到是不是完全二叉树,只要满足最大节点编号等于结点数就可以做到是完全二叉树(需要注意的是:N个点顺序插入空的树,说明第一个插入的点就是根节点,不需要自己去调整)
#include