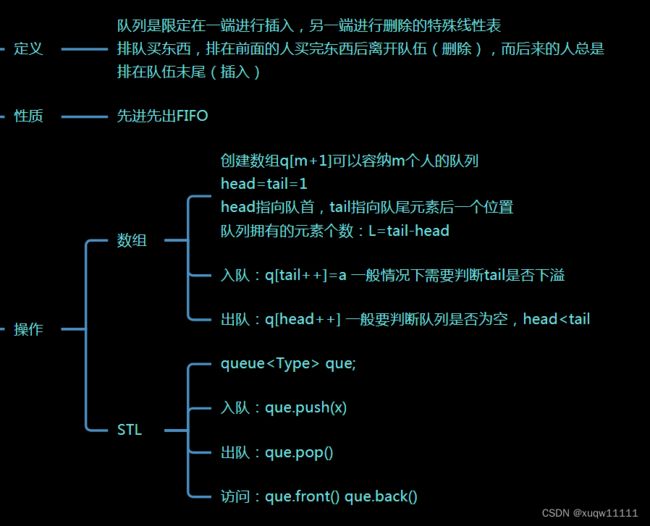
一本通 3.2.1 队列的基本应用
1332:【例2-1】周末舞会
【题目描述】
假设在周末舞会上,男士们和女士们进入舞厅时,各自排成一队。跳舞开始时,依次从男队和女队的队头上各出一人配成舞伴。规定每个舞曲能有一对跳舞者。若两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。现要求写一个程序,模拟上述舞伴配对问题。
【题目分析】
使用两个队列,q1表示男q2表示女,定义两组队列指针 h1,h2,t1,t2
循环m次,先将男的入队,循环n次,将女的入队;
循环k次,将男女队列一起输出,再将男女队列队首元素分别计入相应队列队尾
【代码实现】
#include
using namespace std;
int q1[10005], q2[10005];
int main() {
//input data
int m, n, k;
cin >> m >> n >> k;
int h1 = 1, t1 = 1;
int h2 = 1, t2 = 1;
for (int i = 1; i <= m; i++) {
q1[t1++] = i;
}
for (int i = 1; i <= n; i++) {
q2[t2++] = i;
}
for (int i = 1; i <= k; i++) {
cout << q1[h1] << " " << q2[h2] << endl;
q1[t1++] = q1[h1++];
q2[t2++] = q2[h2++];
}
return 0;
} 1333:【例2-2】Blah数集
【题目描述】
大数学家高斯小时候偶然间发现一种有趣的自然数集合Blah,对于以a为基的集合Ba定义如下:
(1)a是集合Ba的基,且a是Ba的第一个元素;
(2)如果x在集合Ba中,则2x+1和3x+1也都在集合Ba中;
(3)没有其他元素在集合Ba中了。
现在小高斯想知道如果将集合Ba中元素按照升序排列,第N个元素会是多少?
【题目分析】
设定一个队列que[1000005],使用tail指向队尾,h1指向2*x+1的起点数据,h2指向3*x+1的起点数据
初始化: tail=h1=h2=1; que[tail++]=x
重复执行直到 tail>n 循环内部:如果2*que[h1]+1
如果2*que[h1]+1==que[h2]*3+1 h1++;
(两者相等时,可以将h2往后移,h1对应值进入队列,也可以将h1后移,在后面的循环中h2对应值进入队列)
【代码实现】
#include
using namespace std;
int que[1000005];
int x, x1, x2, n;
int main() {
//input data
while (cin >> x >> n) {
int h1 = 1, h2 = 1;
int tail = 1;
que[tail++] = x;
while (tail <= n) {
if (que[h1] * 2 + 1 < que[h2] * 3 + 1)
que[tail++] = que[h1++] * 2 + 1;
else if (que[h1] * 2 + 1 > que[h2] * 3 + 1)
que[tail++] = que[h2++] * 3 + 1;
else
h1++;
}
cout << que[n] << endl;
}
return 0;
} 1334:【例2-3】围圈报数
【题目描述】
有n个人依次围成一圈,从第1个人开始报数,数到第m个人出列,然后从出列的下一个人开始报数,数到第m个人又出列,…,如此反复到所有的人全部出列为止。设n个人的编号分别为1,2,…,n,打印出列的顺序。
【题目分析】
问题本质:经典约瑟夫问题 解题思想:使用数组模拟链表进行模拟
解题过程:定义数组que[105] 数组下标i为人的编号,数组内容que[i]为编号为i的人的下一人的编号
方法1:j指向报数为1的人的上一人,循环执行j=que[j]并进行计数,直到计数为m时,que[j]为出队的人
让j指向他的后面第二个人,跳过一人,que[j]=que[que[j]]
方法2:j指向报数为1的人,循环执行j=que[j]并进行计数,直到计数为m-1时,que[j]为出队的人
让j指向他的后面第二个人,跳过一人,que[j]=que[que[j]],j指向报数为1的人j=que[j]\
【代码实现】
#include
using namespace std;
int que[105];
//第1个人指向第2个人 第2个人指向第3个人
int main() {
//input data
int n, m;
cin >> n >> m;
//创建链表
for (int i = 1; i <= n; i++) {
que[i] = i + 1;
}
que[n] = 1;
//需要出列n个人
int j = n;
for (int i = 1; i <= n; i++) {
int count = 1;
while (count < m ) {
j = que[j];
count++;
}
cout << que[j] << " ";
que[j] = que[que[j]];
// j = que[j];
}
return 0;
} 1335:【例2-4】连通块
【题目描述】
一个n × m的方格图,一些格子被涂成了黑色,在方格图中被标为1,白色格子标为0。问有多少个四连通的黑色格子连通块。四连通的黑色格子连通块指的是一片由黑色格子组成的区域,其中的每个黑色格子能通过四连通的走法(上下左右),只走黑色格子,到达该联通块中的其它黑色格子。
【题目分析】
广度优先搜索
【代码实现】
#include
using namespace std;
int n, m;
int a[105][105];
bool vis[105][105];
int _next[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1},};
void bfs(int x, int y) {
pair que[10005];
int head = 1, tail = 1;
que[tail++] = make_pair(x, y);
while (head < tail) {
x = que[head].first;
y = que[head].second;
for (int i = 0; i <= 3; i++) {
int nx = x + _next[i][0];
int ny = y + _next[i][1];
if (nx < 1 || ny < 1 || nx > n || ny > m) continue;
if (vis[nx][ny] || a[nx][ny] == 0) continue;
vis[nx][ny] = 1;
que[tail++] = make_pair(nx, ny);
}
head++;
}
}
int main() {
//input data
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] == 1 && vis[i][j] == 0) {
ans++;
vis[i][j] = 1;
bfs(i, j); //广度优先搜索
}
}
}
cout << ans << endl;
return 0;
}
1359:围成面积
【题目描述】
编程计算由“*”号围成的下列图形的面积。面积计算方法是统计*号所围成的闭合曲线中水平线和垂直线交点的数目。如下图所示,在10×10的二维数组中,有“*”围住了15个点,因此面积为15
【题目分析】
读取数据到10-*10的数组中,扩展为12*12外圈都为0,使用广度优先搜索记录封闭图形外面0的个数ans1
遍历所有数据,记录1的个数ans2,所以封闭0的面积为12*12-ans1-ans2
【代码实现】
#include
using namespace std;
int n = 10;
int a[15][15];
bool vis[15][15];
int _next[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1},};
int main() {
//input data
int ans1 = 0, ans2 = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> a[i][j];
if (a[i][j] == 1) ans2++;
}
}
//寻找外圈0的个数
pair que[10005];
int head = 1, tail = 1;
ans1++;
vis[0][0] = 1;
que[tail++] = make_pair(0, 0);
while (head < tail) {
int x = que[head].first;
int y = que[head].second;
for (int i = 0; i < 4; i++) {
int nx = x + _next[i][0];
int ny = y + _next[i][1];
if (nx < 0 || ny < 0 || nx > n + 1 || ny > n + 1) continue;
if (vis[nx][ny] == 1 || a[nx][ny] == 1) continue;
vis[nx][ny] = 1;
ans1++;
que[tail++] = make_pair(nx, ny);
}
head++;
}
//包围0的数量为 11*11-ans1-ans2
// cout << ans2 << endl;
cout << (12 * 12 - ans1 - ans2) << endl;
return 0;
}
1360:奇怪的电梯(lift)
【题目描述】
大楼的每一层楼都可以停电梯,而且第i层楼(1≤i≤N)上有一个数字Ki(0≤=Ki≤=N)。电梯只有四个按钮:开,关,上,下。上下的层数等于当前楼层上的那个数字。当然,如果不能满足要求,相应的按钮就会失灵。例如:3 3 1 2 5代表了Ki(K1=3,K2=3,……),从一楼开始。在一楼,按“上”可以到4楼,按“下”是不起作用的,因为没有−2−2楼。那么,从A楼到B楼至少要按几次按钮呢?
【题目分析】
问题本质:每一步有两种扩展选择的广度优先搜索
【代码实现】
#include
using namespace std;
int n, a, b;
int k[205];
pair que[40005];
int head = 1, tail = 1;
bool vis[205];
int main() {
//input data
cin >> n >> a >> b;
for (int i = 1; i <= n; i++) {
cin >> k[i];
}
int min_step = -1;
//使用广搜解决问题
que[tail++] = make_pair(a, 0);
vis[a] = 1;
while (head < tail) {
if (que[head].first == b) {
min_step = que[head].second;
break;
}
int x = que[head].first;
int step = que[head].second;
int nx1 = x + k[x];
if (nx1 >= 1 && nx1 <= n && vis[nx1] == 0) {
vis[nx1] = 1;
que[tail++] = make_pair(nx1, step + 1);
}
int nx2 = x - k[x];
if (nx2 >= 1 && nx2 <= n && vis[nx2] == 0) {
vis[nx2] = 1;
que[tail++] = make_pair(nx2, step + 1);
}
head++;
}
cout << min_step;
return 0;
}
1361:产生数(Produce)
【题目描述】
给出一个整数n(n≤2000)和k个变换规则(k≤15)。规则:
① 1个数字可以变换成另1个数字;
② 规则中,右边的数字不能为零。
例如:n=234,k=2规则为
2 → 5
3 → 6
上面的整数234经过变换后可能产生出的整数为(包括原数)234,534,264,564共4种不同的产生数。
求经过任意次的变换(0次或多次),能产生出多少个不同的整数。仅要求输出不同整数个数。
【题目分析】
方法1:对输入的整数n的每一位i按照规则进行广度优先搜索,确定数字的可能ans[i]
不同整数的个数为![\prod_{i=1}^m ans[i]](http://img.e-com-net.com/image/info8/3adf4a3fa4534375afe61dd127690fd5.gif)
方法2:对设定的规则采用邻接矩阵存储,使用floyed算法求0-9每两个数字的可连通性,
遍历每两个数字并计数ans[i],不同整数的个数为![\prod_{i=1}^m ans[i]](http://img.e-com-net.com/image/info8/3adf4a3fa4534375afe61dd127690fd5.gif)
方法3:并查集 略
方法4:深搜 略
【代码实现】
并查集算法
#include
using namespace std;
int n, k;
struct node {
int sum;
int father;
} a[105];
int find_father(int i) {
if (a[i].father == i) return i;
else return a[i].father = find_father(a[i].father);
}
int main() {
//input data
cin >> n >> k;
//init
for (int i = 1; i <= n; i++) {
a[i].sum = 1;
a[i].father = i;
}
//查找与合并
for (int i = 1; i <= k; i++) {
int x, y;
cin >> x >> y;
int x_father = find_father(x);
int y_father = find_father(y);
if (x_father != y_father) { //右边归顺左边
a[y_father].father = x_father;
a[x_father].sum += a[y_father].sum;
}
}
//统计数据
int ans = 0;
int max_famely = 0;
for (int i = 1; i <= n; i++) {
if (a[i].father == i) {
ans++;
max_famely = max(max_famely, a[i].sum);
}
}
//结果输出
cout << ans << " " << max_famely << endl;
return 0;
}
广搜算法
#include
using namespace std;
int rule[10][16];
int que[1005];
bool vis[10];
int head, tail;
int ans[10];
int main() {
//input data
int n, k;
cin >> n >> k;
for (int i = 1; i <= k; i++) {
int x, y;
cin >> x >> y;
rule[x][++rule[x][0]] = y;
}
//0-9 bfs
for (int i = 0; i <= 9; i++) {
head = tail = 1;
memset(vis, 0, sizeof(vis));
que[tail] = i;
tail++;
vis[i] = 1;
while (head != tail) {
int num = que[head];
head++;
ans[i]++;
for (int j = 1; j <= rule[num][0]; j++) {
if (vis[rule[num][j]] == 0) {
que[tail] = rule[num][j];
tail++;
vis[rule[num][j]] = 1;
}
}
}
}
int maxans = 1;
while (n != 0) {
maxans *= ans[n % 10];
n /= 10;
}
cout << maxans;
return 0;
} floyed算法
#include
using namespace std;
bool rule[10][10];
int ans[10];
int main() {
//input data
int n, k;
cin >> n >> k;
for (int i = 0; i <= 9; i++) {
rule[i][i] = 1;
}
for (int i = 1; i <= k; i++) {
int x, y;
cin >> x >> y;
rule[x][y] = 1;
}
//floyed
for(int k=0;k<=9;k++){
for(int i=0;i<=9;i++){
for(int j=0;j<=9;j++){
rule[i][j]=rule[i][j]||(rule[i][k]&&rule[k][j]);
}
}
}
//scan and update ans
for(int i=0;i<=9;i++){
for(int j=0;j<=9;j++){
if(rule[i][j]) ans[i]++;
}
}
int maxans = 1;
while (n != 0) {
maxans *= ans[n % 10];
n /= 10;
}
cout << maxans;
return 0;
} 1362:家庭问题(family)
【题目描述】
有n个人,编号为1,2,……n,另外还知道存在K个关系。一个关系的表达为二元组(α,β)形式,表示α,β为同一家庭的成员。
当n,k和k个关系给出之后,求出其中共有多少个家庭、最大的家庭中有多少人?
例如:n=6,k=3,三个关系为(1,2),(1,3),(4,5)
此时,6个人组成三个家庭,即:{1,2,3}为一个家庭,{4,5}为一个家庭,{6}单独为一个家庭,第一个家庭的人数为最多。
【题目分析】
方法1:对每个家庭成员i的进行广度优先搜索,记录家庭成员人数a[i],如果家庭成员没有遍历过ans++,
最大的家庭成员数:max(a[i]) 1<=i<=n ,家庭数为ans;
方法2:对每个家庭成员i进行并查集记录(父亲father和家族人数sum),如果两个人不是同一个father,右边y归顺左边x,
a[y_father].father=x_father, a[x_father].sum+=a[y_father].sum; 访问每个家庭成员i,如果a[i].father=i,说明是祖先,统计
祖先的个数即为家族的个数,统计祖先自带家族成员的个数最大值,即为最大家族的人数。
方法3:深搜 与广搜类似 略
方法4:连通性判断floyed算法,可以建立邻接矩阵,统计每个家庭成员i可以连通的成员数量最大值即为最大家族的人数,使用
标记数组访问每个i的连通性,如果存在连通ans++,标记i和i的连通 标记数组为1,否则继续进行遍历未被标记的i
【代码实现】
#include
using namespace std;
int rule[105][105];
int que[105];
bool vis[105];
int head, tail;
int main() {
//input data
int n, k;
cin >> n >> k;
for (int i = 1; i <= k; i++) {
int x, y;
cin >> x >> y;
rule[x][++rule[x][0]] = y;
rule[y][++rule[y][0]] = x;
}
//Everyone bfs
int family = 0;
int maxans = 0;
int ans = 0;
for (int i = 1; i <= n; i++) {
if (vis[i]) continue;
ans = 0;
family++;
head = tail = 1;
que[tail] = i, tail++;
ans++;
vis[i] = 1;
while (head != tail) {
int num = que[head];
head++;
for (int j = 1; j <= rule[num][0]; j++) {
if (vis[rule[num][j]] == 0) {
que[tail] = rule[num][j], tail++;
vis[rule[num][j]] = 1;
ans++;
}
}
}
maxans = max(maxans, ans);
}
cout << family << " " << maxans;
return 0;
} #include
using namespace std;
int n, k;
struct node {
int sum;
int father;
} a[105];
int find_father(int i) {
if (a[i].father == i) return i;
else return a[i].father = find_father(a[i].father);
}
int main() {
//input data
cin >> n >> k;
//init
for (int i = 1; i <= n; i++) {
a[i].sum = 1;
a[i].father = i;
}
//查找与合并
for (int i = 1; i <= k; i++) {
int x, y;
cin >> x >> y;
int x_father = find_father(x);
int y_father = find_father(y);
if (x_father != y_father) { //右边归顺左边
a[y_father].father = x_father;
a[x_father].sum += a[y_father].sum;
}
}
//统计数据
int ans = 0;
int max_famely = 0;
for (int i = 1; i <= n; i++) {
if (a[i].father == i) {
ans++;
max_famely = max(max_famely, a[i].sum);
}
}
//结果输出
cout << ans << " " << max_famely << endl;
return 0;
}
1418:猴子选大王
【题目描述】
由经典约瑟夫问题改成。
有N个猴子,编号从1到N。每个猴子对应一个正整数Xi,表示如果从编号为i的猴子开始报数,需要数到Xi。
这N个猴子围成一圈,从第一个开始报数,数到第1个猴子对应的正整数X1的猴子出队,然后从它的下一位继续从1开始报数,数到对应的Xi时出队,如此循环直到剩下一个猴子,最后剩下的那个猴子就是猴子们选出的大王。
例如:
N=5,Xi=5,对应为:1,2,3,4,5
出队的顺序为:1,3,4,5
【题目分析】
使用数组a[i]记录每个猴子的报数为1时,下次需要出列的数字k
报数出列的过程与经典约瑟夫问题相同,不同的是只要有人出列,就要更新k的数值
最后在循环外设置记录变量last1,在循环内满足出列人数为n时,记录下出列人的编号
【代码实现】
#include
using namespace std;
int monkey[1000005];
int num[1000005];
int main() {
//input data
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
monkey[i] = i + 1;
cin >> num[i];
}
monkey[n] = 1;
int k = 0;
int p = n;
int start = num[1];
while (k < n - 1) {
int say = 0;
while (say < start - 1) {
p = monkey[p];
say++;
}
monkey[p] = monkey[monkey[p]];
start = num[monkey[p]];
k++;
}
cout << p << endl;
return 0;
}