AcWing算法基础(3)
一、双指针算法
1,算法分析:
所谓双指针算法,也就是用两个指针去扫描数组,有可能是扫描同一个数组,也有可能是两个不同的数组,凡是用到类似方法都可以称为双指针,双指针算法的优点就在于能够把用暴力解决的所需时间复杂度为 ![]() 的方法优化成
的方法优化成 ![]() ,大大提高了问题的解决效率。其算法模板如下:
,大大提高了问题的解决效率。其算法模板如下:
for (int i = 0, j = 0; i < n; i ++ )
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
//常见的问题:
// (1) 对于一个数组,用两个指针维护一段区间
// (2) 对于两个数组,维护某种次序,比如归并排序中合并两个有序序列的操作2,例题1,799.最长连续不重复子序列
(1)题目描述:
给定一个长度为n的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
(2)数据范围:
所有的整数均小于10e5,n小于10e5。
(3)问题样例
输入:
5
1 2 2 3 5
输出:
3
// 3指的是数组中的“235”(4)问题分析:
先考虑暴力求解的方法,再思考i和j分别有没有单调关系,再进一步用双指针来优化。
我们用 i 来遍历[i:0→n]数组,用 j 来指向能够在左端且距离当前 i 指向的数字最远的数字,根据分析,我们先说结论:在i往后移的时候,j 绝不可能往前移动,也就是 j 和 i 之间具有单调性。随后再来证明一下这个结论.
我们来思考一下,当固定 i 不动 ![]() ,我们何时移动 i ,那必然是 j 已经移动到了此时的''最佳''位置
,我们何时移动 i ,那必然是 j 已经移动到了此时的''最佳''位置![]() ,当 j 再远离 i 的时候已经指向了一个与此时 i 指向的数字相同的数字了
,当 j 再远离 i 的时候已经指向了一个与此时 i 指向的数字相同的数字了 ![]() ,此时我们才需要移动 i 来找下一个数字
,此时我们才需要移动 i 来找下一个数字 ![]() 的''最佳长度'',那么这个时候新的
的''最佳长度'',那么这个时候新的 ![]() 的左端必定包含的有
的左端必定包含的有 ![]() ,如果此时 j 是向后移动,就会使 i,j 之间直接出现重复的数字,故 j 只能向后移动,也就是说 i 往后移动的时候,j 不会往前移动,二者具有单调性。
,如果此时 j 是向后移动,就会使 i,j 之间直接出现重复的数字,故 j 只能向后移动,也就是说 i 往后移动的时候,j 不会往前移动,二者具有单调性。
两个指针的功能定义好了,剩下的就是''check(j,i)''这个判断的问题了,我们要检查的是当前的j和i之间的数字是否有重复,根据问题的数据范围,我们就单开一个数组s[N]记录下每个数字(如果数字很大的话,就可以用C++的哈希表来解决),看代码:
(5)代码
#include
#define N 100010
int n;
int q[N],s[N];
int max(int x, int y)
{
return x>y?x:y;
}
int main()
{
scanf("%d",&n);
for(int i = 0 ;i < n ; i ++)
scanf("%d",q+i);
int ans = 0;
int j = 0;
for(int i = 0;i < n ; i ++)
{
s[ q[i] ] ++;
while(j < i && s[ q[i] ] > 1)
{
s[ q[j] ]--;
j++;
}
//☆while循环是为了在遇到两个相同的数字的时候,更新j,使得j指向该数字第一次出现的下一位
ans=max( ans, i-j+1 );
}
printf("%d",ans);
return 0;
} 其中,while循环这一步请多花时间思考,用样例模拟一下。
3,例题2,800. 数组元素的目标和
(1)题目描述:
给定两个有序数组A(数组长度n),B(数组长度m),以及一个目标值x,数组下标从0开始, 请求出满足A[i]+B[j]=x,的数对(i,j)题目保证有唯一解。
(2)数据范围:
数组长度n,m不超过10e5,数组元素的值不超过10e9,保证同一个数组无相同元素。
(3)问题样例
输入样例:(第一行分别为n,m,x)
4 5 6
1 2 4 7
3 4 6 8 9
输出样例:
1 1(4)问题分析:
先从暴力循环开始考虑,无非两层for循环,组合所有的A[i],B[j],时间复杂度为O(m*n),因为A,B数组分别是严格单调上升序列,所以我们可以利用这一点来优化算法,使用双指针。
注意:这是一个经典的双序列双指针题,经典的操作。
我们不妨用i指针对A数组从前往后扫,用j指针对B数组从后往前扫,A[i]+B[j]≠x的时候无非就两种情况,A[i]+B[j]>x,或者是A[i]+B[j] 给定长度分别为n,m的序列,a,b,请你判断 a 序列是否为 b 序列的子序列。子序列指序列的一部分项按原有次序排列而得的序列,如 序列长度均不大于10e5,序列元素均不大于10e9 这个题一画图就可以找到i和j的单调关系,根据子序列的定义,如果我们找得到所有a序列中的元素,且把这些元素在b数组中下标组成一个新的数组的话,这个新的数组就是一个递增数组,通过进一步的分析,我们知道当指向序列a的指针向后移动的时候,要想满足子序列定义,指向序列b的指针不可能向前移动,只能向后移动,所以i,j之间有着单调性。 我们只需要遍历b数组(遍历a数组理论上是可行,但是我写代码卡住了),当满足条件a[i]==b[j]的时候就让i++,最后只需要判断一下i是否等于n(或者从1开始n+1)即可。 用于处理值域很大,但是这个值域内的数个数很少,零零散散的几个点,而有些题我们需要用这些点的下标来做,但是又不能开一个匹配值域的数组,比如: 把值与值很分散的数据保序的映射到下标为0和自然数递增序列这个过程就叫做离散化 那我们需要解决的问题有两点 把数组的每一个值映射到他的下标,下标就是他映射的值 ,实现离散化的本质就是二分的方法去找到想要离散化的数据在该数组中的下标位置 区间合并的功能就是将若干个有交集的区间合并成一个这些区间并集的新区间,也就是包含了这些区间的新区间。(5)代码
#include 4,例题3,2816. 判断子序列
(1)题目描述:
![]() 是序列
是序列 ![]() 的子序列。
的子序列。(2)数据范围:
(3)问题样例:
输入样例:
3 5
1 3 5
1 2 3 4 5
输出样例:
Yes (4)问题分析:
(5)代码
#include二、位运算
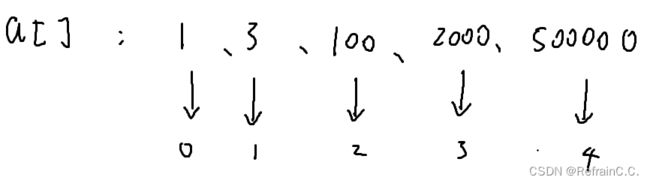
三、离散化
四、区间合并