k-d Tree算法

1.概述

  本文介绍一种用于高维空间中的快速最近邻和近似最近邻查找技术——Kd- Tree(Kd树)。Kd-Tree，即K-dimensional tree，是一种高维索引树形数据结构，常用于在大规模的高维数据空间进行最近邻查找(Nearest Neighbor)和近似最近邻查找(Approximate Nearest Neighbor)，例如图像检索和识别中的高维图像特征向量的K近邻查找与匹配。

2.Kd-tree

2.1 二叉搜索树

Kd-Tree，即K-dimensional tree，是一棵二叉树，树中存储的是一些K维数据。在一个K维数据集合上构建一棵Kd-Tree代表了对该K维数据集合构成的K维空间的一个划分，即树中的每个结点就对应了一个K维的超矩形区域（Hyperrectangle）。

先回顾一下二叉搜索树（Binary Search Tree）的相关概念和算法。

二叉搜索树(Binary Search Tree，BST)有如下性质：

1）若它的左子树不为空，则左子树上所有结点的值均小于它的根结点的值；

2）若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值；

3）它的左、右子树也分别为二叉搜索树；

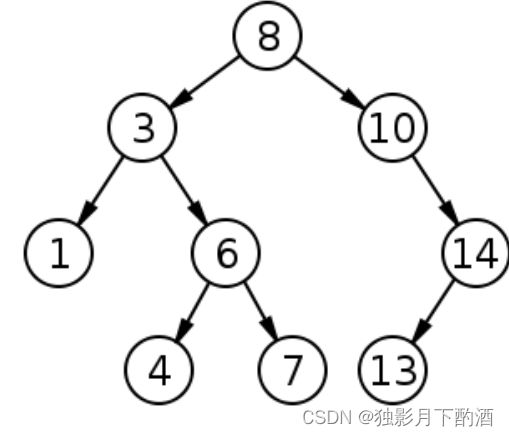
如图是一棵二叉搜索树，其满足BST的性质。

Q： 给定一个1维数据集合，怎样构建一棵BST树呢？

根据BST的性质就可以创建，即将数据点一个一个插入到BST树中，插入后的树仍然是BST树，即根结点的左子树中所有结点的值均小于根结点的值，而根结点的右子树中所有结点的值均大于根结点值。

将一个1维数据集用一棵BST树存储后，当查询某个数据是否位于该数据集合中时，只需要将查询数据与结点值进行比较然后选择对应的子树继续往下查找即可，查找的平均时间复杂度为：$O(logN)$，最坏的情况下是$O(N)$。

Q:如果要处理的对象集合是一个K维空间中的数据集，那么是否也可以构建一棵 类似于1维空间中的二叉查找树呢？

答案是肯定的，只不过推广到K维空间后，创建二叉树和查询二叉树的算法会有一些相应的变化(后面会介绍到两者的区别)， 这就是下面要介绍的Kd-tree算法。

k-d树算法可以分为两大部分，一部分是有关k-d树本身这种数据结构建立的算法，另一部分是在建立的k-d树上如何进行最邻近查找的算法。

2.2 Kd-Tree的构建算法

k-d树是一个二叉树，每个节点表示一个空间范围。下表给出的是k-d树每个节点中主要包含的数据结构。

域名	数据类型	描述
Node-data	数据矢量	数据集中某个数据点，是n维矢量（这里也就是k维）
Range	空间矢量	该节点所代表的空间范围
split	整数	垂直于分割超平面的方向轴序号
Left	k-d树	由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right	k-d树	由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent	k-d树	父节点

从k-d树节点的数据类型的描述可以看出构建k-d树是一个逐级展开的递归过程。构建k-d树伪码。

输入：数据点集Data-set和其所在的空间Range

输出：Kd，类型为k-d tree

1.If Data-set为空，则返回空的k-d tree

2. 调用节点生成程序

3. 确定split域：对于所有描述子数据(特征矢量)，统计它们在每个维上的数据方差。以SURF特征为例，描述子为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率；

4. 确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set’ = Data-set\Node-data（除去其中Node-data这一点）。

5. dataleft = {d属于Data-set’ && d[split] ≤ Node-data[split]}

   ​ Left_Range = {Range && dataleft}

   dataright = {d属于Data-set’ && d[split] > Node-data[split]}

   ​ Right_Range = {Range && dataright}

6. left = 由（dataleft，Left_Range）建立的k-d tree，即递归调用createKDTree（dataleft，Left_Range）。并设置left的parent域为Kd；

   right = 由（dataright，Right_Range）建立的k-d tree，即调用createKDTree（dataleft，Left_Range）。并设置right的parent域为Kd。

举例说明KD-Tree的构建过程：

假设有6个二维数据点$\{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\}$，数据点位于二维空间内（如图1中黑点所示）。k-d树算法就是要确定图1中这些分割空间的分割线(多维空间即为分割平面，一般为超平面)。

数据维度只有2维，所以简单地给 $x，y$ 两个方向轴编号为 $0,1$，也即 $split=\{0,1\}$。

• 1. 确定split域的首先该取的值。
  • 分别计算 $x，y$ 方向上数据的方差得知 $x$ 方向上的方差最大，所以split域值首先取0，也就是 $x$ 轴方向；
• 2. 确定Node-data的域值。
  • 根据x轴方向的值$2,5,9,4,8,7$排序选出中值为$7$，所以$Node-data=(7,2)$。这样，该节点的分割超平面就是通过$(7,2)$并垂直于$split=0$( $x$ 轴)的直线$x=7$；

  注：$2,4,5,7,8,9$在数学中的中值为$(5+7)/2=6$，但因该算法的中值需在点集合之内，所以本文中值计算用的是$len(points)//2=3,points[3]=(7,2)$

• 3. 确定左子空间和右子空间。
  • 分割超平面 $x=7$ 将整个空间分为两部分，如图2所示。$x<=7$ 的部分为左子空间，包含3个节点$\{(2,3)，(5,4)，(4,7)\}$；另一部分为右子空间，包含2个节点$\{(9,6)，(8,1)\}$。

上述的构建过程结合下图可以看出，构建一个k-d tree即是将一个二维平面逐步划分的过程。

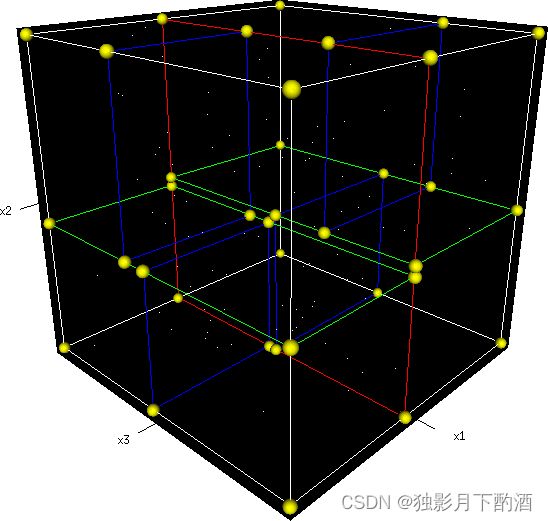
从三维空间来看一下k-d tree的构建及空间划分过程。

首先，边框为红色的竖直平面将整个空间划分为两部分，此两部分又分别被边框为绿色的水平平面划分为上下两部分。最后此4个子空间又分别被边框为蓝色的竖直平面分割为两部分，变为8个子空间，此8个子空间即为叶子节点。

如下为k-d tree的构建代码：

def kd_tree(points, depth):
    if 0 == len(points):
        return None
    cutting_dim = depth % len(points[0])
    medium_index = len(points) // 2
    points.sort(key=itemgetter(cutting_dim))
    node = Node(points[medium_index])
    node.left = kd_tree(points[:medium_index], depth + 1)
    node.right = kd_tree(points[medium_index + 1:], depth + 1)
    return node

2.3 k-d树上的最邻近查找算法

  在k-d树中进行数据的查找也是特征匹配的重要环节，其目的是检索在k-d树中与查询点距离最近的数据点。先以一个简单的实例来描述最邻近查找的基本思路。

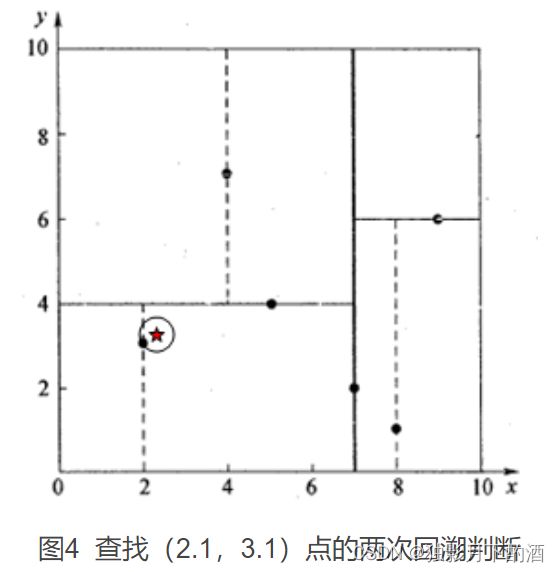
星号表示要查询的点$(2.1,3.1)$。

  通过二叉搜索，顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点 $(2,3)$。 而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻，还需要进行’回溯’操作：算法沿搜索路径反向查找是否有距离查询点更近的数据点。

  先从 $(7,2)$ 点开始进行二叉查找，然后到达 $(5,4)$，最后到达 $(2,3)$，此时搜索路径中的节点为$<(7,2),(5,4),(2,3)>$，首先以$(2,3)$作为当前最近邻点，计算其到查询点 $(2.1,3.1)$ 的距离为 $0.1414$，然后回溯到其父节点$(5,4)$，并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以 $(2.1,3.1)$ 为圆心，以 $0.1414$ 为半径画圆，如图4所示。发现该圆并不和超平面 $y=4$ 交割，因此不用进入 $(5,4)$ 节点右子空间中去搜索。

如果查找点为$(2，4.5)$，那是怎么样的过程呢？

  先进行二叉查找，先从 $(7,2)$ 查找到 $(5,4)$ 节点，在进行查找时是由 $y=4$ 为分割超平面的，由于查找点为 $y$ 值为 $4.5$，因此进入右子空间查找到$(4,7)$，形成搜索路径 $<(7,2),(5,4),(4,7)>$，取$(4,7)$ 为当前最近邻点，计算其与目标查找点的距离为 $3.202$。然后回溯到 $(5,4)$，计算其与查找点之间的距离为 $3.041$。以 $(2，4.5)$ 为圆心，以$3.041$为半径作圆，如图5所示。可见该圆和$y=4$超平面交割，所以需要进入 $(5,4)$ 左子空间进行查找。此时需将 $(2,3)$ 节点加入搜索路径中得 $<(7,2)，(2,3)>$。回溯至$(2,3)$叶子节点，$(2,3)$ 距离 $(2,4.5)$ 比 $(5,4)$ 要近，所以最近邻点更新为$(2,3)$，最近距离更新为$1.5$。回溯至 $(7,2)$，以 $(2,4.5)$ 为圆心 $1.5$ 为半径作圆，并不和 $x=7$ 分割超平面交割，如图6所示。至此，搜索路径回溯完。返回最近邻点 $(2,3)$，最近距离 $1.5$。

k-d树查询算法的伪代码如下：

输入：Kd， //k-d tree类型

  	target //查询数据点

输出：nearest， //最邻近数据点

  	 dist   //最邻近数据点和查询点间的距离

1. If Kd为NULL，则设dist为infinite并返回

2. 进行二叉查找，生成搜索路径

//Kd-point中保存k-d tree根节点地址

 Kd_point = &Kd；   

//初始化最近邻点

 nearest = Kd_point -> Node-data； 

 while（Kd_point）

		//search_path是一个堆栈结构，存储着搜索路径节点指针		

 　　push（Kd_point）到search_path中；

/*** If Dist（nearest，target） > Dist（Kd_point -> Node-data，target）

 　　　　nearest = Kd_point -> Node-data；  //更新最近邻点

 　　　　Max_dist = Dist(Kd_point，target）； //更新最近邻点与查询点间的距离 ***/

​ //确定待分割的方向

 　　s = Kd_point -> split； 

		//进行二叉查找           

 　　If target[s] <= Kd_point -> Node-data[s]  

 　　　　Kd_point = Kd_point -> left；

 　　else

 　　　　Kd_point = Kd_point ->right；

//注意：二叉搜索时不比计算选择搜索路径中的最邻近点，这部分已被注释

 nearest = search_path中最后一个叶子节点；

 Max_dist = Dist（nearest，target）；  //直接取最后叶子节点作为回溯前的初始最近邻点

3. 回溯查找

while（search_path != NULL）

 　　back_point = 从search_path取出一个节点指针；  //从search_path堆栈弹栈

​ //确定分割方向

 　　s = back_point -> split；          

​ //判断还需进入的子空间

 　　If Dist（target[s]，back_point -> Node-data[s]） < Max_dist  

 　　　　If target[s] <= back_point -> Node-data[s]

​ //如果target位于左子空间，就应进入右子空间

 　　　　　　Kd_point = back_point -> right；

 　　　　else

​ //如果target位于右子空间，就应进入左子空间

 　　　　　　Kd_point = back_point -> left;  

 　　　　将Kd_point压入search_path堆栈；

 　　If Dist（nearest，target） > Dist（Kd_Point -> Node-data，target）

​ //更新最近邻点

 　　　　nearest = Kd_point -> Node-data；    

​ //更新最近邻点与查询点间的距离

 　　　　Min_dist = Dist（Kd_point -> Node-data,target）；

3.总结

  Kd树在维度较小时（比如 $20、30$），算法的查找效率很高，然而当数据维度增大(例如：$K\ge 100$)，查找效率会随着维度的增加而迅速下降。假设数据集的维数为 $D$，一般来说要求数据的规模 $N$ 满足 $N>>2$ 的 $D$ 次方，才能达到高效的搜索。

代码实现参考：https://github.com/guoswang/K-D-Tree

本文仅仅作为个人学习记录，不作为商业用途，谢谢理解。

参考：

1.https://www.cnblogs.com/eyeszjwang/articles/2429382.html

2.https://leileiluoluo.com/posts/kdtree-algorithm-and-implementation.html

3.https://www.cnblogs.com/aTianTianTianLan/articles/3902963.html