数据结构(c语言)-2
线性表的定义和特点
由n(n>=0)个数据特性相同(各个元素所占空间一样大)的元素构成的有限序列称为线性表(其中n为表长)。如:学生基本信息中每一个学生为一个数据元素,包括:学号,姓名,性别,籍贯,专业等等数据项。
线性表中元素的个数n(n>=0)定义为线性表的长度,n=0是称为空表。
注:线性表里的元素是有限的。
当a1是第一个元素,an是第n个元素,ai是第i个元素,称i为数据元素ai在线性表里的位序。
a1是表头元素,an是表尾元素。
对于非空的线性表或线性结构,其特点是:
- 存在唯一的一个被称作“第一个”的数据元素;
- 存在唯一的一个被称作“最后一个”的数据元素;
- 除第一个之外,结构中的每个数据元素均只有一个前驱;
- 除最后一个之外,结构中的每一个数据元素均只有一个后继。
线性表的基本操作
ADT 线性表
数据对象:{a1,a2,······,an},其中每一个数据元素的类型都是Data type。
InitList(&L)
作用:构造一个空的线性表L。
DestroyList(&L)
作用:销毁线性表L
ClearList(&L)
作用:将线性表L重置为空表。
ListEmpty(L)
作用:判断线性表L是否为空表,是返回true,否返回false。
ListLength(L)
作用:返回线性表L中数据元素个数。
GetElem(L,i,&e)
作用:用e返回线性表L中第i个数据元素的值。注:其中(1<=i<=ListLength)
LocateElem(L,e)
作用:返回一个已经存在的线性表L中一第个的值与e相同的元素在线性表L中的位置,如果这样的数据元素不存在,则返回值为0.
PriorElem(L,cyr_e,&next_e)
作用:如果cur_e是L的数据元素,且不是第一个,则用pre_e返回其前驱,否则操作失败,pre_e无定义。
NextElem(L,cur_e,&next_e)
作用:如果cur_e是L的数据元素,且不是最后一个,则用next_e返回其后续,否则操作失败,next_e无定义。
ListInsert(&L,i,e)
作用:在L中第i个位置之前插入新的数据元素e,L的长度+1。注:其中(1<=i<=ListLength(L)+1)
ListDelete(&L,i)
作用:删除L的第i个元素,L的长度-1。
TraverseList(L)
作用:对线性表L进行遍历,在遍历过程中对L的每一个节点访问一次。
注:上述线性表标注为“L”的线性表,此操作的前提条件都是:线性表L已存在。
e指的是数据元素,并没有指明数据的基本类型。
顺序表的定义
顺序表---用顺序存储的方式实现线性表顺序存储。把逻辑上相邻的存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的领结关系来体现(在c语言中可以用sizeof(Elem Type)这个函数来计算一个数据元素的大小。)
顺序表的实现--静态分配
#define MaxSize 10 //定义最大长度
typedef struct{
Elemtype data[MaxSize]; //用静态的数组存放数据元素
int length; //顺序表的当前长度
}sqlist; //顺序表的类型定义  如图是data这个数组里面的内存分布,各个数据元素分配连续的储存空间,其大小为MaxSize*sizeof(Elem type)+sizeof(int)。
如图是data这个数组里面的内存分布,各个数据元素分配连续的储存空间,其大小为MaxSize*sizeof(Elem type)+sizeof(int)。
//基本操作--初始化一个顺序表
void InitList(sqList &l){
for(int i=0;i上述中对所有数据元素设置默认初始值这个是可以省略的,因为我们在静态定义顺序表的时候,多定义了一个length这一个变量,他的作用就是来计算这个顺序表里面有多少个数据元素,我们将来在用printf打印函数时候就直接用这个length来规定打印数据元素的个数即可。
注:length这个变量必须要初始化。
上述就是用静态分布来定义一个顺序表,但是这个方式有它的缺点,就是静态变量所分布的空间一旦开辟就无法改变,是无法进行更改的。(存储空间是静态的)。
如果我们想一开始就开辟一块大的空间,那这快空间很容易造成空间的浪费,所以以静态的方式定义顺序表是有局限性的。
顺序表的实现--动态分配
#define InitaSize 10 //顺序表的初始长度
typedef struct{
ElemType *data; //指示动态分配数组的指针(指向的顺序表的第一个数据元素,也就是malloc函数开辟
//空间的第一个位置的地址
int MaxSize; //顺序表的最大容量
int lengrh; //顺序表的当前长度
}Seqlist; //顺序表的类型定义(动态分配的方式)在c中我们使用malloc函数和free函数来申请和释放一块内存空间
L.data=(ElemType*)malloc(sizeof(ElemType)*InitSize):
//申请开辟一块空间上述(ElemType *)是类型的强制转换,我们只需要将我们这块开辟的空间强制转化为我们需要的数据元素的类型即可。
例:
使用动态分布的方式来实现顺序表,虽然在内存大小方面可以动态变化,但是在空间和时间上的开销就比静态分布的方式实现要多。所以我们在选择实现顺序表的方式时候,要根据实际情况来选择我们需要的方式来实现。
顺序表的特点:
- 随机访问,即可以在O(1)时间内找到第i个元素(因为顺序的数据元素是连续存放的,所以我们只需要知道第一个元素的地址就可以找到后面元素。)
- 存储密度高,每个节点只存储数据元素。(在链式存储里面,不仅仅要存储数据元素,还要存房指针)
- 拓展容量不方便,静态分配直接不能拓展,动态分配虽然能拓展但是对于时间和空间的开销相对较大)
- 插入,删除操作不方便,需要移动大量的元素。

顺序表的基本操作--插入
在一个顺序表里面插入一个数据元素,我们用代码实现的基本思想是,加入我们要在第i个数据元素前插入一个数据元素,那么我们只需要将第i个以及第i个以后的数据元素往后移动一位,然后再把需要的数据元素插进去即可。如图所示:
代码实现:
#define MaxSize 10 //定义最大长度
typedef struct{
int data[MaxSize]; //用静态的数组存放数据元素
int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
void ListInsert(SqList &L,int i,int e){
for(int j=L.length;j>=i,j--) //将第i个元素及之后的元素后移
{
L.data[j]=L.data[j-1]; //在位置i处放入e
L.data[i-1]=e; //长度加一
l.length++;
}
int main(){
SqList L; //声明一个顺序表
InitList(L); //初始化顺序表
//此处省略插入元素的代码
ListInsert(L,3,3);
return 0;
}我们知道基操的实现可以让别人更好的使用我们所创造的数据结构。那么下面我们用代码来实现一下顺序表里的插入数据元素的操作。对于上述代码的实现,为了代码的健壮性我们可以进行一下更改:
bool ListInsert(SqList &L,int i,int e){
if(i<1||i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=MaxSize) //判断这个顺序表的储存空间是否已经满了
return false;
for(int j=L.length;j>=i,j--) //将第i个元素及之后的元素后移
{
L.data[j]=L.data[j-1]; //在位置i处放入e
L.data[i-1]=e; //长度加一
l.length++;
}
return true;
}注:在c99之后C语言增加了bool类型的原始数据类型。可以和其他数据类型一样正常使用。只能用来存放两个值:true (1) 和 false (0) 。用来规定真假。(在C语言中零表示假,非零表示真)
bool类型是在头文件
顺序表的基本操作---删除
基本思想是,假设要删除第i个元素,把第i个元素删除之后再把第i个元素后面的数据元素往前移一个单位即可。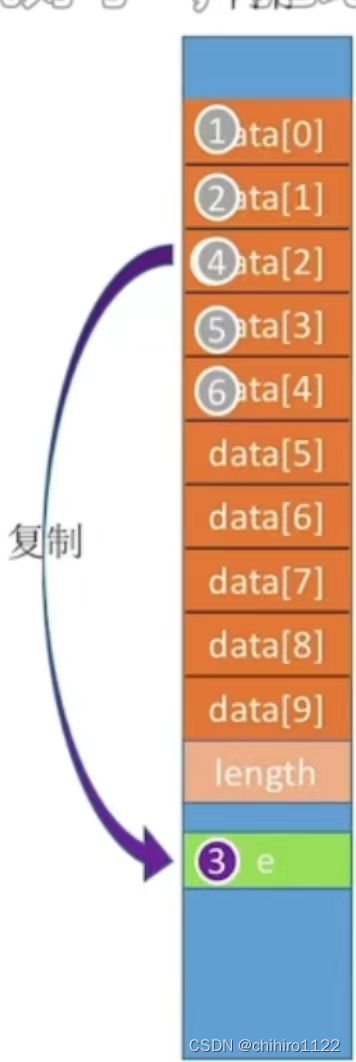
代码实现:
bool ListInsert(SqList &L,int i,int e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e=L.data[j-1]; //将被删除的元素赋值给e
for(int j=i;j顺序表的基本操作--查找
按位查找(查找第i个位置的元素的值)
GetElem(L,i):按位查找操作,获取表L中第i个位置的数据元素的值。
代码实现:
#define MaxSize 10 // 静态分布的方式实现顺序表的查找
typedef struct{
ElemType data [MaxSize};
int length;
}SqList;
ElemType GetElem(SqList L,int i){ //这个函数的返回值与你的定义顺序表里面的数据类型一致
return L.data[i-1];
}#define InitSize 10 //顺序表的初始长度(以动态分布的方式实现顺序表的查找)
typedef struct{
ElemType *data; //指示动态分配内存空间首元素的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
}SeqList; //顺序表的类型定义
ElemType GetElem(SeqList L,int i){
return L.data[i-1]; // malloc开辟的空间也可以像数组一样来进行访问
}
根据动态分配的时对malloc函数开辟空间的数据元素的访问,就可以知道为什么在使用malloc函数时,为什么要在前面进行与数据元素类型相同的强制类型转换。
按位查找要求知道元素的下标(位置)所以我们一般使用按值查找
按值查找
找到表中与传入参数值相同的元素
#define InitSize 10 //以动态分配方式定义顺序表
typedef struct{
ElemType *data;
int MaxSize;
int length;
}length;
int locateElem(SeaList L,ElemType e ){
for(int i=0;ilength;i++){
if(L>data[i]==e)
return i+1; //数组下标为i的元素值等于e,返回位序i+1
}
return 0; //退出循环,查找失败 上述在判断值是否相等时用到了“==”这个运算符,这个运算符c语言中是不能两边都用变量的,但是在c++中可以使用运算符重载的方式进行使用。
顺序表的缺点:
- 空间不够需要扩容时,扩容是有消耗的。
- 头部或者是中间的插入,删除,需要挪动,挪动数据也是有消耗的。
- 为了避免频繁扩容,一般是一次性按照倍数(一般2倍)去扩,可能存在移动的空间浪费。
单链表的定义(实现)
了解单链表:单链表与顺序表的不同之处在于:他的每一个节点都是离散存放的,而且每一个节点除了存放数据元素以外还要存储下一个数据元素所在的位置指针。我们之前阐述了关于顺序表的有缺点,单链表
优点:
- 不要求大片的连续空间,对于容量的改变相对于顺序表要容易许多。
- 更合理的使用了空间,不用了就释放空间,按照需要申请空间。
缺点:
- 不可以随机存取--(用下标直接访问第i个)------随机访问是有价值的,有些算法需要结构随机访问这个特性--比如二分查找,优化的快排等等······
- 而且要耗费一些内存来存储下一个数据元素的位置指针。
对于单链表的容量拓展,因为这里的每一个节点在内存中是离散分布的,而且他们通过指针相连,在内存中没有固定顺序,所以我们在对单链表的容量进行拓展时,只需要在内存中划出一小片空间存储增加的数据元素就行。
单链表的代码定义(实现)
satruct LNode{ //定义单链表结点类型
ElemType data; //每个结点存放一个数据元素
struct LNode *next; //指针指向下一个结点
};
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个结点存放一个数据元素
struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;
struct LNode *p =(struct LNode *)malloc(sizeof(struct LNode));
//增加一个新的结点:在内存中申请一个结点所需要的空间,并用指针p指向这个结点
typedef struct LNode LNode; //把“struct LNode”重命名为“LNode”
typedef struct LNode *LinkList; //用LinkList来表示一个指向这个结构体的指针
typedef<数据类型><别名> //数据类型的重命名
上述的LNode * L // 声明一个指向单链表第一个结点的指针 ····1
是等价于
LinkList L的 //声明一个指向单链表第一个结点的指针 ······2
对于急需一个简单的单链表可以进行下面简单创建:
int main(){
struct ListNode* n1 = (struct ListNode*)malloc(sizeof(struct ListNode));
struct ListNode* n2 = (struct ListNode*)malloc(sizeof(struct ListNode));
struct ListNode* n3 = (struct ListNode*)malloc(sizeof(struct ListNode));
struct ListNode* n4 = (struct ListNode*)malloc(sizeof(struct ListNode));
n1->val = 7;
n2->val = 7;
n3->val = 7;
n4->val = 7;
n1->next = n2;
n1->next = n3;
n1->next = n4;
n1->next = NULL;
return 0;
}对于你的写的单链表的操作函数,要用来测试你写的函数电话,用这个来快速创建一个单链表,是非常方便的。
单链表的初始化
不带头结点的单链表
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个结点存放一个数据元素
struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;
bool InitList(LinkList &L){
L = NULL; //空表,暂时还没有结点
return ture;
}
void test(){
LinkList L; //声明一个指向单链表的指针
//初始化一个空表
InitList(L);
//后续基本操作
}同样的我们在使用时候需要判断单链表是否为空
bool Empty(LinkList L){ //·······1
if (L == NULL)
return ture;
else
return false;
bool Empty(LinkList L){ //········2
return (L==NUll);
}带头结点的单链表
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个结点存放一个数据元素
struct LNode *next; //指针指向下一个结点
}LNode,*LinkList;
bool InitList(LinkList &L){
L = (LNode *) malloc(sizeof(LNode)); //分配一个头结点
if (L==NULL0 //内存不足,分配失败
return false;
L->next = NUll; //头结点之后暂时还没有结点
return ture;
}
void test(){
LinkList L; //声明一个指向单链表的指针
//初始化一个空表
InitList(L);
//后续基本操作
}
//判断一个单链表是否为空(带头结点)
bool Empty(LinkListL{
if (L->next == NULL)
return ture;
else
return false;
}需要注意的是,这里比刚刚多声明了一个头结点,这个头结点的data里面没有存储任何东西,只是next指针指向下一个结点,这个头结点只是为了后续更好的一些操作。
对于上述两种对于单链表的初始化,不带头结点的初始化方式在写代码的时候更麻烦,如下操作可以看出。
单链表的插入和删除操作
单链表的插入操作
单链表的尾插(c语言)
typedef int SLTDateType;
typedef struct SListNode
{
SLTDateType data;
stryct SListNode* next;
}SLYNode;
void SListPushBack(SKTNode** pphead, SLTDateType x) //尾插
{
SLTNode* newnode = (SLTDode*)malloc(sizeof(SLTNode));
newnode->next = NULL;
if(*pphead == NULL)
{
*pphead = newnode;
}
else
{
//找到尾结点
SLTNode* tail = *pphead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newnode;
}
}
void SListPrint(SLTNode* phead)
{
SLTNode* cur = phead;
while (cur != NULL)
{
printf("%d->",cur->data);
cur = cur->next;
}
}
void TestSList1()
{
SLTNode* plist = NULL;
SListPushBack(&plist,1);
SListPushBack(&plist,2);
SListPushBack(&plist,3);
SListPushBack(&plist,4);
SListPrint(plist);
}单链表的头插(无头结点)
申请一块空间,这块空间就是在第一个结点之前插入的新的结点,然后让这个结点的newnode指针指向之前第一个结点,然后把plist也就是头指针改为新插入结点的地址,在把需要的值传入新的结点就完成了对无头结点单链表的头插操作。我们还要考虑一种情况,就是当plist单链表的头指针为空也就是链表里面一个结点都没有的时候,其实我们这个方法是可以实现这种特殊情况的。
假设这个单链表里面没有结点,那么当我们插入一个结点的时候,就让这个结点的newnode指针指向下一个结点地址也就是空地址,然后再让plist指针指向这个新的结点也可以实现头插的操作。
代码实现:
SLTNode* BuyListNode(SLTDateType x) //实现插入新结点操作的函数
{
SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
if(newnode == NULL) //判断malloc函数开辟空间是否开辟成功
{
printf("malloc fail/n\n");
exit(-1); //直接结束掉程序,后续不在执行
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
void SListPushFront(SLTNode** pphead, SLTDateType x) //头插
{
SLTNode* newnode = BuyListNode(x);
newnode->next = *pphead;
*pphead = newnode;
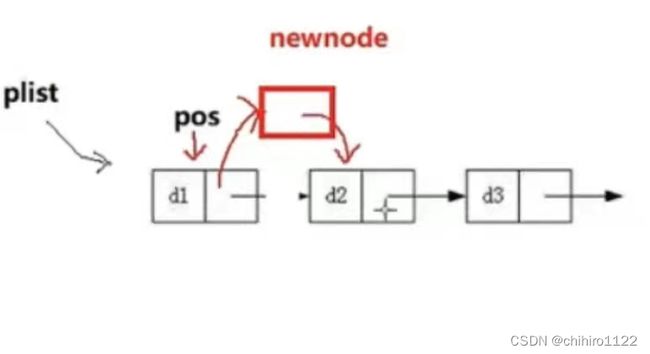
} 单链表的指定位置的后插
假设我们要在表中的第i个结点之后插入一个新的结点:
我们可以先定义一个新的结点,在中间插入一个新的结点主要就是对结点中next指针的改变比较重要,我们在定义好一个新的结点(newnode)的时候,必须先让这个newnode这个结点的next指针原本插入之前表的第i+1个结点的位置,然后再让第i个结点的next指针指向这个新的结点的地址。这样做的原因的是原本第i+1个结点的位置指针是保存在第i个结点里的,如果我们反过来操作的话,那之前保存的地址会被替换掉。
代码实现:
void SListInsertAfter(SLTNode* pos,SLTDateType x)
{
SLTnode*newnode = BuyListNode(x); //创建一个新的结点
newnode->next = pos->next; //让这个新的结点的next指针指向pos的下一个结点
pos->next = newnode; //让pos的结点的next指针指向这个新的结点
}之前写过在pos位置的前一个位置插入新的结点,那么这两种方法有什么不一样呢?
其实这两种方法虽然看上去差不多,但在复杂度上面差很多,如果实在pos位置之前插入一个新的结点,因为这个是单链表,没有办法通过链表来找到上一个结点的位置,所以我们只能再多定义一个指针来存储上一个结点的位置,而且必须用循环的方式来寻找pos在表中的位置,否则找不到上一个元素,如此他的时间复杂度时O(n)。
那么对于另一个方法呢,他不需要用循环来寻找pos,直接用pos指针找到位置即可在后面插入,他的时间复杂度时O(1)。
单链表结点的删除
单链表的尾删
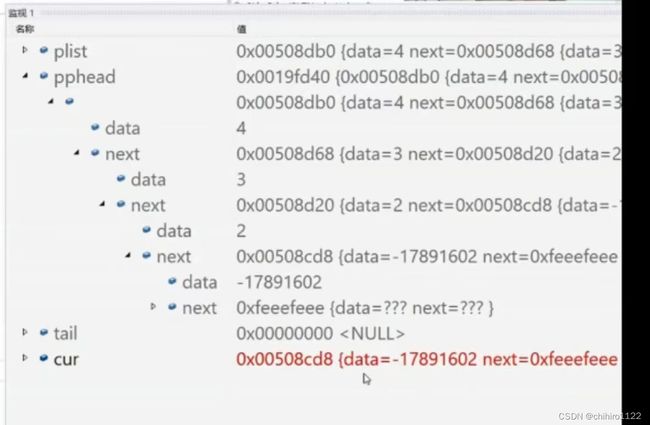
利用循环找到最后一个结点,也就是当结构体中的next指针为空的时候,找到就把这个结点的空间给释放。需要注意的是
···· 首先尾删不仅仅是尾部结点的删除还有删除结点的上一结点里的next指针必须置空,如果不置空我们在之后打印的时候,虽然需要删除的结点已经删除,但是上一结点的next指针仍然指向原本删除结点的位置,而这个位置已经被系统给置为随机值,经过调试如下所示:
对需要删除的结点的前一个结点的next指针置空的这个效果的实现,我们可以再在函数里定义一个指针--prev指针,这个指针在tail指针(也就是上述用来寻找尾结点的函数里的局部变量)向下一个结点跳跃之前就把tail的地址传给prev备份,当tail指针找到尾结点的时候,prev指针就存储的是tail上一个结点的地址,就实现了单链表访问上一结点的效果。
····然后是尾删的极限情况,当尾删删除到这个链表里一个结点都没有的时候,我们是需要将这个链表的头指针给置空的,表示这个链表是空的,而要实现这个效果,我们在用函数实现尾删操作的时候,就需要用一个二级指针,对这个头指针进行传参和修改的功能。
注:解释1:上述两种解决需要删除结点的前一个结点的next指针的置空的方法都存在一个问题,就是当结点只有一个或者没有结点的时候,代码会崩。我们先讨论当链表为空的时候,
“prev->next = NUll“上述这段代码的prev指针是NULL,对空指针的解引用是错误的操作。然后是链表只有一个结点的时候,这时候“prev->next = NUll”也是一样的,访问不到下一个结点,达不到删除的目的。
void SListPushBack(SLTNode** pphead)
{
if(*pphead == NULL) //代码健壮性
{
return;
}
assert(*pphead != NULL); //和上述一样的效果
if((*pphead)->next == NULL) //解释1
{
free(*pphead);
*pphead = NULL;
}
else
{
SLTNode* prev = NULL;
SLTNode* tail = *pphead;
while (tail->next) //这种写法等价于->while(tail->next != NULL)
{
prev = tail; //让prev指针指向tail指针跳跃之前的所指向的地址
tail = tail->next;
}
free(tail); //把要删除的结点的内存给释放
tail = NULL;
prev->next = NUll; //将删除结点的上一结点的next指针置空
}
}
对需要删除的结点的前一个结点的next指针置空的这个效果的实现,还有一种方法,就是让tail访问下一个结点来作为查找的目标,如下面代码所示:
while(tail->next->next) //从头指针的第三个位置开始查找
{
tail = tail->next;
}
free(tail->next);
tail->next = NULL;
}单链表的头删
关于单链表的头删需要注意的点是头指针应该指向被删结点的下一个结点,而且在实现这个代码的时候,应该先指再删,因为保存下一结点的指针next在被删除的结点中。
void SListPushFront(SLTNode** pphead)
{
assert(*pphead != NULL);
SLTNode* next = (*pphead)->next; //保存下一个结点的地址
free(*pphead); //释放掉被删除结点的空间
*pphead = next; //让头指针指向下一个
}指定位置的删除结点
指定一个结点的删除,包括上述-头删和-尾删除和中间删除的情况,中间删除的话,就把上一个结点的next指针指向那个下一个结点就行。
代码实现:
void SListErase(SLTNode** pphead, SLTNode* pos)
{
assert(pphead);
assert(pos); //判断传入的pos指针是否为空 ,但其实下面就已经判断了,这里只是想
//要提醒一下当pos为空的情况是可能会报错的
if(*pphead == pos)
{
pphead = pos->next;
free(pos);
}
else
{
SLTNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = pos->next;
free(pos);
// pos = NULL; //虽然对形参的置空没有意义,但是要有这样的习惯
}
}整个单链表的删除
这里只需要从第一个结点按照单链表的指针指向顺序一个个删除,当向下移动指针,指针指向NULL时就结束即可实现。需要注意的是这里一样是要先指后删的。
代码实现:
void SListDestory(SLTNode** pphead)
{
assert(pphead);
SLTNode* cur = *pphead;
while (cur)
{
SLTNode* next = cur->next;
free(cur);
cur = next;
}
*pphead = NULL;
}
单链表的查找
按值查找
这个代码的实现很简单,就用一个循环查找一个与输入的参数值相同的结点。但是我们要考虑的问题是,当这个结链表里面有多个值相同的结点时,该如何一同找出。其实要实现这个效果也非常的简单,假设我们要找到表中指为2的结点,我们可以先找到第一个值为2的结点,然后用用一个循环去一个一个的挨着找接下来的值为2的结点。
代码实现:
void SListFind(SLTNode* phead,SLTDateType x)
{
SLTNode* cur = phead;
while (cur)
{
if (cur->data == x)
{
return cur;
}
else
{
cur = cur->next;
}
}
return NULL;
}
void TestSList()
{
SLTNode* plist = NULL;
SListPushFront(&plist,1);
SListPushFront(&plist,2);
SListPushFront(&plist,3);
SListPushFront(&plist,2);
SListPushFront(&plist,4);
SLTNode* pos = SListFind(plist, 2);
int i = 1;
while (pos)
{
printf(第%d个pos结点:%->%d\n",i++,pos,pos->data); //打印值为2的结点
pos = SListFind(pos->next,2); //找到值为2的结点并把这个结点的指针传给pos存储
}
}
int main()
{
TestSList();
}查找之后的修改
假如入我们找到值为3的结点,想把这个结点的值改为30的话,改如何实现呢?
在上述代码实现查找的前提下
代码实现:
pos = SListFind(plist,3);
if(pos)
{
pos->data = 30;
}
SListprint(plist);这里主要想要强调的是SListFind这个查找的函数不仅可以进行查找的功能还可以利用它进行修改,上述代码如果想要修改多个结点的话,可以用循环来修改。
单链表的缺陷
单纯的单链表的尊山查找的意义不大
单链表更多的是去做更复杂的数据结构的子结构,如:哈希桶,邻接表
用链表存储数据还是双链表相对好用。
循环链表
循环链表有单链表和双链表的循环,
单链表的循环链表就是,原本表里的最后一个结点的next指针是指向NULL的,现在指向第一个结点的位置。
双链表的循环链表就是,原本表里的第一个结点的prev指针指向最后一个结点,最后一个结点的next指针指向第一个结点。
双向链表
对于单链表的局限性,我们这里定义一种新的链表--双链表。他的每一个节点不仅仅存储下一个节点的地址,还存储了上一个结点的地址。在我们单链表里面使用的快慢指针,多定义一个指针来存储上一个结点的地址等等这些麻烦的操作都不需要了,因为表里本身就有前后结点的地址。
对于第一个结点的prev指针,和最后一个结点的next指针是指向NULL的。
但是,对于时间的节省,换来的是空间的增大,它相比于单链表要多存储差不多一倍的指针。但是其实双链表也是优势大于劣势的。
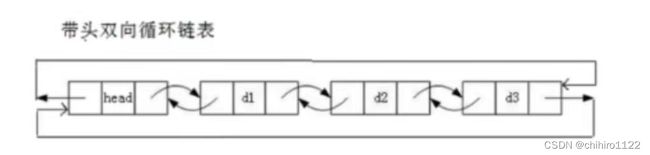
如下面的带头结点的循环双链表,虽然在结构上复杂了很多,但是在使用这种链表实现操作比之前学的无头单向非循环链表跟简单。
对于双链表的链表为空的情况,他的哨兵位的头结点的next和prev指针都指向它自己。对于带哨兵位头指针的链表在实现函数操作的时候,引入参数时是不需要使用二级指针的,但是没有头结点就像之前单链表一样如果需要修改头指针就需要二级指针来对其进行修改。
双链表的代码创建
定义其实很简单,就比单链表多存储一个prev指针存储上一个结点的位置。
代码实现:
#pragma once
#include
#include
#include
typedef int LTDateType;
struct ListNode
{
LTDateType data;
struct ListNode* next;
struct ListNode* prev;
}LTNode;
void ListInit(LTNode* phead); //初始化
{
//头结点
phead = (LTNode*)malloc(sizeof(LTNode));
phead->next = phead;
phead->prev = phead;
return phead;
}
void ListPushBack(LTNode* phead,LTDateType x); //尾插
{
LTNOde* newnode = (LTNOde*)malloc(sizeof(LTNode));
newnode->data = x;
tail->next = newnode;
newnode->prev = tail;
newnode->next = phead;
phead->prev = newnode;
}
void TestList()
{
LTNode* pList = NULL;
ListInit(pList);
ListPushBack(pList,1); //尾插
ListPushBack(pList,2);
ListPushBack(pList,3);
ListPushBack(pList,4);
}
int main(){
return 0;
} 上述实现双链表的创建的时候,是使用在一个空节点之后使用尾插的方式实现,
创建一个函数,作用是创建一个结点空间来实现插入操作
void BuyListNode(LTDateType x)
{
LTNode* newnode = (LTNode*)malloc(sizeofLTNode));
newnode->data = x;
newnode->next = NULL;
newnode-prev = NULL;
return newnode;
}循环双链表的尾插
这个操作非常的简单,只需要在第一个结点的prev指针找到最后一个结点,然后把之前最后一个结点的next指针指向新插入的结点,把新结点的prev指针指向最后一个结点,next指针指向第一个结点,最后把第一个结点的prev指针指向新结点,就完成了尾插操作。操作不复杂,时间复杂度也很小,不用像之前那样用一个循环来寻找最后一个结点在来插入。
我们发现,当这个表为空的时候,也就是头指针phead指向NULL的时候,这个代码同样可以实现尾插,不影响操作。所以我们没必要在之前加 “ assert(phead)”这种类似的代码判断传入的头指针是否为空。
同样,整个操作没有对头指针进行改变,只对表中的结点的指针进行修改,所以在函数中没必要使用二级指针或者是返回值的操作来修改头指针。
代码实现:
void ListPushBack(LTNode* phead,LTDateType x); //尾插
{
LTNOde* newnode = (LTNOde*)malloc(sizeof(LTNode));
newnode->data = x;
tail->next = newnode;
newnode->prev = tail;
newnode->next = phead;
phead->prev = newnode;
}
void ListPrint(LTNode* phead) //打印这个表
{
assert(Phead);
LTNode* cur = phead->next;
whild (cur != phead)
{
printf("&d",cur->data);
cur = cur->next;
}
printf("\n");
}循环双链表的尾删
双链表的尾删就是最后一个结点删除了,再把第一个结点的prev指向倒数第二个结点,倒数第二个结点的next指向第一个结点。
需要注意的是,free释放时机需要考虑,如果要像下列例子一样先free掉结点的话就先要把上一个结点的位置给储存起来,如果想先把修改结点的信息在free就得最后在free。
还有一个问题是当这个双链表有头结点的时候不能把头结点给删了,所以要对特殊情况进行判断。
void ListPopBack(LTNode* phead)
{
assert(phead);
asserrt(phead->next != phead); //当两个相对的时候是只有头结点的时候
LTNode* tail = phead->prev;
LTNode* tailprev = tail->prev; //在free之前先存储一下删除结点的上一个结点的地址
free(tail);
tailprev->next = phead;
phead->prev = tailprev;
}带头结点循环双链表的头插和头删
头插
在第一个结点(头结点之后一个结点)位置插入一个新节点,其实很简单,只需要修改对应的链接顺序就行,这里我们使用了之前创建的BuyListNode函数,来快速实现新结点空间的创建。
void ListPushFront(LTNode* phead,LTDateType x)
{
assert(phead);
LTNode* newnode = BuyListNode(x);
LTNode* next = phead->next;
phead->next = newnode;
newnode->prev = phead;
newnode->next = next;
next->prev = newnode;
}
头删
同样的处理好连接关系插入即可,因为是删除,所以要考虑不能删除头结点的情况。
void ListPopfront(LTNode* phead)
{
assert(phead);
assert(phead->next != phead);
LTNode* next = phead->next;
LTNode* nextNext = next->next;
phead->next = nextNext;
nextNext->prev = phead;
free(next);
}到头结点循环双链表的查找
LTNode* ListFind(LTNode* phead,LTDataType x)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
if(cur->data == x)
{
return cur;
}
cur=cur->next;
}
return NULL; //没找到,返回一个空
}指定位置插入结点
对于带头结点循环双链表的指定位置插入就要简单很多了,并不用像单链表一样多定义个指针来存储上个结点的位置。直接创建一个新的结点然后改链接关系就行了。
需要注意的是,如果你不用下列代码里的posPrev指针来存储上一个结点的位置,就要注意下面改链接的顺序,必须先把指定结点-pos的上一个结点的链接先改了,再去改去改pos指向结点的链接。不然就不能通过pos指针找到上一个结点。
void ListInsert(LTNode* pos,LTDateType x)
{
assert(phead);
LTnode* posPrev = pos->prev;
LTNode* newnode = BuyListNode(x);
posPrev->next = newnode;
newnode->prev = posPrev;
newnode->next = pos;
pos->prev = newnode;
}因为上述函数传入的参数是指针形式的,所以在传入参数之前需要用之前实现的查找操作来寻找位置,再以参数的形式传给ListInsert函数。
int main(){
LTNode* pos = ListFind(plist,2)l
if(pos)
{
ListInsert(pos,x);
}
}对于带头结点循环双链表,写好指定位置的插入函数之后,这个函数也可以实现我们之前实现的头插和尾插的操作,这就是循环双链表带来的便利之处。
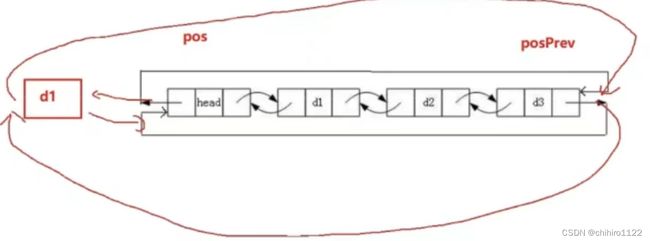
比如:用ListInsert函数实现尾插,就是按照之前的推算,他的画图位置是在头结点的前面的,但是实际上,他的位置与尾结点的位置是一致的,因为头指针不变,只是把循环的链接改变了。
尾插的ListInsert函数的实现就是让pos指针指向头结点也就是头指针指向的结点,即:直接调用
ListInsert(phead,x);
对于头插的实现,也是一样的,只不过pos指向的是第一个结点,也就是头结点后一个结点,即;
ListInsert(phead->next,x);
尾插图 如下图:
指定位置的结点删除
同样的就是链接的改变
代码实现:
void ListErase(LTNode* pos)
{
assert(pos);
LTNode* poPrev = pos->prev;
LTNode* posNext = pos->next;
posPrev->next = posNext;
posNext->prev = posPrev;
free(pos);
pos = NULL;
}同样的,因为上述函数传入的参数时指针,所以需要用之前实现的查找函数来查找一下位置。
int main(){
LTNode* pos = ListFind(plist,2)l
if(pos)
{
listErase(pos);
}
}由此不难想出指定位置的删除也可以实现头删和尾删的操作。
尾删:ListErase(phead->prev);
头删:ListErase(phead->next);
这就是到头结点循环双链表带来的好处,虽然在创建和定义的实现比单链表麻烦,但是在操作的实现上,真的方便很多,但是单链表也不是毫无用处,单链表的用处一般的都是与其他结构一起出现带来的好处,一般是作为一些跟复杂的结构的子结构出现的。比如哈希表中每一个节点下面挂一串数据,这一串数据没必要使用双链表来实现,单链表就行实现他的全部作用。
整个双链表的删除
整个双链表的删除和单链表的大同小异,只不过需要注意的是,这里使用了一级指针,对于最后一步注释掉的头指针置空是不可实现的,但是整个双链表的操作函数传入的都是一级指针,为了参数一致性,我们不使用二级指针,这样方便其他人使用,只不过使用了一级指针的删除,就要在函数外部对头指针手动删除。
void ListDestroy(LTNode* phead)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
LTNode* next = cur->next;
free(cur);
cur = next;
}
free(phead)
//phead = NULL; //头指针的置空
}对于顺序表和链表的选择总结:
这两个结构看似是链表更好用,但是实际上这两个结构各有各的优势,很难说出谁更优,严格俩说他们两个是相辅相成的两个结构。
顺序表:
优点:支持随机访问,需要随机访问机构支持算法可以很好的适用。
cpu高速缓存利用率更高。
缺点:头部或者中部的插入删除效率低。O(n)
他是连续的物理空间,空间不够之后需要增容,增容有一大程度的消耗。比如:假设我们要扩大两倍的空间,假设原本的空间大小是10字节,想要扩容就要新创建一个20字节的空间,然后把原本空间里面的数据给复制进去,在释放之前的空间。
为了避免频繁的增容,一般都会按倍数去增容,用不完可能存在一定的空间浪费。
链表:(假设是带头指针循环双链表)
优点:任意位置插入,删除效率高。O(1)
按照自己的需要申请,释放空间。
缺点:
不支持随机访问。(用下标访问)意味着有些算法(快排,一些排序,二分查找)在这种结构上不适用。
链表存储一个值,同时要存储链接指针,也有一定的消耗,这对于不大的链表这个影响几乎没有,但是不排除电脑不行的情况。
cpu高速缓存命中率更低