10.图和树基础

一、基本介绍

1.图

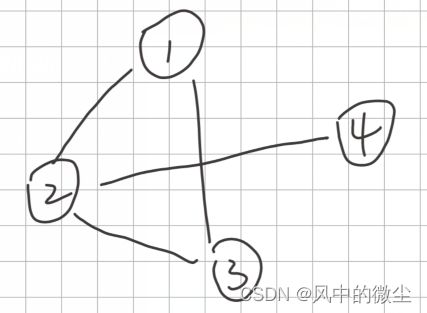
图描述的是一些个体之间的关系。这些个体之间既不是前驱后继的顺序关系，也不是祖先后代的层次关系，而是错综复杂的网状关系。我们一般用图$G=(V,E)$来表示，$V$表示结点，$E$表示边。

• 根据边是否有权值，分为带权图和不带权图，也可将不带权图视为权重都为$1$的图。

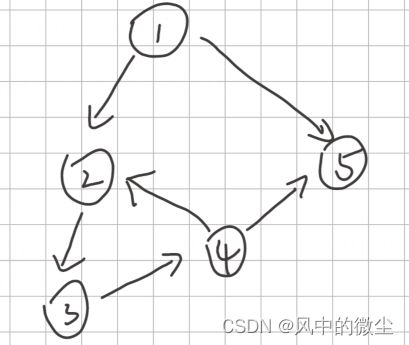
• 根据边是否有方向，分为有向图和无向图。

• 根据稠密程度（边的条数$|E|$与$|V{|}^2$）的关系，分为稠密图和稀疏图。

2.树

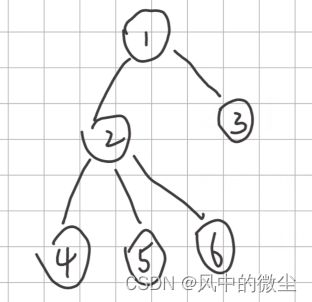
树是一种特殊的图，它满足$|V|=|E|+1$。将其中一个结点作为根节点，表示所有结点的祖先。

对于树上的连边，靠近根节点的结点被叫做父结点，远离根节点的结点被叫做子节点。一个结点只有一个父节点，但可以有多个子节点。具有相同父节点的结点互称为兄弟结点。

二、一些性质

1.度

对于无向图来说，一个结点的度等于该结点所连的边数。

对于有向图来说，一个结点的入度等于连向该结点的边数，一个结点的出度等于连出该结点的边数。

2.子图

对于图$G=(V,E)$和图$G^{\prime }=(V^{\prime },E^{\prime })$来说，如果满足$V^{\prime }\in V,E^{\prime }\in E$，则$G^{\prime }$是$G$的子图。

3.连通性

• 对于无向图$G=(V,E)$来说：

  • 如果任意两个结点之间，都有一条通路，那么该图是一个连通图。
  • 无向边构成的树一定是一个连通图，且任意两点之间仅存在一条简单路径（无重边）。
  • 如果一个子图$G^{\prime }$是一个连通图，则称$G^{\prime }$为连通子图

• 对于有向图$G=(V,E)$来说：

  • 如果任意两个结点之间，都有一条通路，那么该图是一个强连通图。
  • 如果一个子图$G^{\prime }$是一个连通图，则称$G^{\prime }$为强连通子图（强连通分量）。

三、图的表示

1.邻接矩阵

邻接矩阵即使用一个二维数组来完全表示一个图。

• 在稠密图的情况下，我们更多使用邻接矩阵来表示图。
• 如果两个点之间存在多条边，那么可能邻接矩阵将并不适用。
• 邻接矩阵在稀疏图的情况下，容易受点数限制。

$mp[u][v]=w$表示存在一条从结点$u$到结点$v$的权重为$w$的边。

对于无向边，可以视为两条方向相反、连接结点相同的边。

const ll maxn=1010;
ll n,m,mp[maxn][maxn];
int main()
{
	scanf("%lld%lld",&n,&m);
	for(ll i=1;i<=m;i++)
	{
		ll u,v,w;
		scanf("%lld%lld%lld",&u,&v,&w);
		mp[u][v]=w;
        //mp[v][u]=w;
	}
	
	return 0;
}

2.邻接表

邻接表在表示稀疏图时非常紧凑，节省空间，所以成为通常用来表示图的方法。

数组$p[u]$表示结点$u$的最后一条边，$p[u]==-1$则表示点$u$没有别的边了。$t$表示边的数量。

数组$e[t]$表示第$t$条边的所有信息，其中$v$表示边的终点，$w$表示边的权重，$next$表示具有同样起点的另一条边。

const ll maxn=100010;
struct node
{
	ll v;
	ll w;
	ll next;
}e[maxn*2];
ll n,m,p[maxn],t=0;
void insert(ll u,ll v,ll w)
{
	e[t].v=v;
	e[t].w=w;
	e[t].next=p[u];
	p[u]=t++;
}
int main()
{
	memset(p,-1,sizeof(p));
	scanf("%lld%lld",&n,&m);
	for(ll i=1;i<=m;i++)
	{
		ll u,v,w;
		scanf("%lld%lld%lld",&u,&v,&w);
		insert(u,v,w);
        //insert(v,u,w);
	}
	
	return 0;
}

四、图的遍历

1.邻接矩阵

#include 
#include 
#include 
#include 

using namespace std;
typedef long long ll;
const ll maxn=1010;
ll n,m,mp[maxn][maxn];
void dfs(ll u,ll pre)
{
    cout<<"u="<<u<<endl;
    for(ll i=1;i<=n;i++)
    {
        if(i!=pre)
            dfs(i,u);
    }
}
int main()
{
	scanf("%lld%lld",&n,&m);
	for(ll i=1;i<=m;i++)
	{
		ll u,v,w;
		scanf("%lld%lld%lld",&u,&v,&w);
		mp[u][v]=w;
        mp[v][u]=w;
	}
	
	return 0;
}

2.邻接表

#include 
#include 
#include 
#include 

using namespace std;
typedef long long ll;
const ll maxn=100010;
struct node
{
	ll v;
	ll w;
	ll next;
}e[maxn*2];
ll n,m,p[maxn],t=0;
void insert(ll u,ll v,ll w)
{
	e[t].v=v;
	e[t].w=w;
	e[t].next=p[u];
	p[u]=t++;
}
void dfs(ll u,ll pre)
{
    cout<<"u="<<u<<endl;
    for(ll i=p[u];i!=-1;i++)
    {
        ll v=e[i].v;
        if(v!=pre)
            dfs(v,u);
    }
}
int main()
{
	memset(p,-1,sizeof(p));
	scanf("%lld%lld",&n,&m);
	for(ll i=1;i<=m;i++)
	{
		ll u,v,w;
		scanf("%lld%lld%lld",&u,&v,&w);
		insert(u,v,w);
        insert(v,u,w);
	}
	
	return 0;
}

五、作业