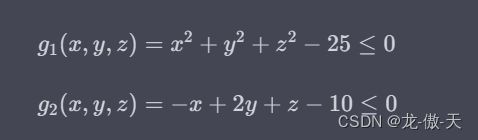遗传算法为主的多目标优化算法
求解一个简单的多目标函数优化问题。在这个问题中,我们的目标是最小化一个三维函数,并同时最小化两个约束条件。代码将使用 Python 语言和 DEAP 库来实现。
首先,我们需要定义问题的目标函数和约束条件。假设我们的目标函数是 Rosenbrock 函数,其形式为:
其中,a,b,和c是常数,我们可以将它们设置为 1。我们还需要两个约束条件,分别为:
下面是 Python 代码实现:
import math
from deap import base, creator, tools
a = 1
b = 100
c = 100
def rosenbrock(x):
return (a - x[0])**2 + b*(x[1] - x[0]**2)**2 + c*(x[2] - x[0]**3)**2
def constraint1(x):
return x[0]**2 + x[1]**2 + x[2]**2 - 25
def constraint2(x):
return -x[0] + 2*x[1] + x[2] - 10
接下来,我们需要定义问题的优化目标和约束条件。在这个问题中,我们需要最小化目标函数,并同时满足两个约束条件。我们可以使用 DEAP 库来定义问题的适应度函数:
creator.create("FitnessMin", base.Fitness, weights=(-1.0, -1.0))
creator.create("Individual", list, fitness=creator.FitnessMin)
toolbox = base.Toolbox()
toolbox.register("attr_float", random.uniform, -5, 5)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_float, n=3)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("evaluate", rosenbrock)
toolbox.decorate("evaluate", tools.DeltaPenalty(constraint1, 10000.0))
toolbox.decorate("evaluate", tools.DeltaPenalty(constraint2, 10000.0))
在适应度函数中,我们使用 weights 参数来指定多目标优化问题的权重。由于我们需要最小化两个目标函数,因此我们将 weights 设置为 (-1.0, -1.0)。同时,我们使用 DeltaPenalty 函数来处理约束条件,将违反约束条件的个体的适应度值惩罚为一个非常大的数值。
接下来,我们需要定义进化算子。在这个问题中,我们使用交叉和变异来产生新的个体,并使用多目标竞赛选择来选择下一代的个体。具体实现实现如下:
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=1, indpb=0.1)
toolbox.register("select", tools.selNSGA2)
def main():
pop = toolbox.population(n=100)
cxpb = 0.5
mutpb = 0.2
ngen = 100
for g in range(ngen):
offspring = [toolbox.clone(ind) for ind in pop]
for child1, child2 in zip(offspring[::2], offspring[1::2]):
if random.random() < cxpb:
toolbox.mate(child1, child2)
del child1.fitness.values
del child2.fitness.values
for mutant in offspring:
if random.random() < mutpb:
toolbox.mutate(mutant)
del mutant.fitness.values
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
pop = toolbox.select(offspring + pop, k=len(pop))
return pop
在这个代码中,我们使用一个种群大小为 100 的种群,使用交叉概率为 0.5 和变异概率为 0.2。我们运行 100 代进化,并使用 NSGA-II 算法进行多目标优化。在每一代中,我们先对种群进行交叉和变异操作,产生新的个体,然后对新的个体进行适应度函数的评估,最后使用 NSGA-II 算法选择下一代个体。
最后,我们可以运行代码,并输出 Pareto 最优解集合:
if __name__ == "__main__":
pop = main()
pareto_front = tools.ParetoFront()
pareto_front.update(pop)
print(pareto_front)
这段代码将输出 Pareto 最优解集合,其中每个解都是一个三维向量,代表最小化目标函数和约束条件的结果。
总的来说,这个代码展示了如何使用遗传算法为主的多目标优化算法来解决一个简单的多目标函数优化问题。在实际应用中,我们需要根据具体的问题和需求进行参数调整和算法改进,以达到最佳的搜索效果。