B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第1张图片](http://img.e-com-net.com/image/info8/5cfe28c500034f50a7591f4b4c9c453e.jpg)
【机器学习入门与实践】入门必看系列,含数据挖掘项目实战:数据融合、特征优化、特征降维、探索性分析等,实战带你掌握机器学习数据挖掘
- 专栏详细介绍:【机器学习入门与实践】合集入门必看系列,含数据挖掘项目实战:数据融合、特征优化、特征降维、探索性分析等,实战带你掌握机器学习数据挖掘。
- 本专栏主要方便入门同学快速掌握相关知识。声明:部分项目为网络经典项目方便大家快速学习,后续会不断增添实战环节(比赛、论文、现实应用等)
专栏订阅:数据挖掘-机器学习专栏
主要讲解了数据探索性分析:查看变量间相关性以及找出关键变量;数据特征工程对数据精进:异常值处理、归一化处理以及特征降维;在进行归回模型训练涉及主流ML模型:决策树、随机森林,lightgbm等。同时重丶讲解模型验证、特征优化、模型融合等。
本项目码源链接:https://www.heywhale.com/mw/project/64367e0a2a3d6dc93d22054f
机器学习码源专栏链接:https://www.heywhale.com/home/column/64141d6b1c8c8b518ba97dcc
相关文章:
特征工程详解及实战项目【参考】
数据挖掘---汽车车交易价格预测[一](测评指标;EDA)
数据挖掘机器学习---汽车交易价格预测详细版本[二]{EDA-数据探索性分析}
数据挖掘机器学习---汽车交易价格预测详细版本[三]{特征工程、交叉检验、绘制学习率曲线与验证曲线}
数据挖掘机器学习---汽车交易价格预测详细版本[四]{嵌入式特征选择(XGBoots,LightGBM),模型调参(贪心、网格、贝叶斯调参)}
数据挖掘机器学习---汽车交易价格预测详细版本[五]{模型融合(Stacking、Blending、Bagging和Boosting)}
数据挖掘机器学习[六]---项目实战金融风控之贷款违约预测
数据挖掘机器学习[七]---2021研究生数学建模B题空气质量预报二次建模求解过程
1.简介:
比赛要求参赛选手根据给定的数据集,建立模型,二手汽车的交易价格。来自 Ebay Kleinanzeigen 报废的二手车,数量超过 370,000,包含 20 列变量信息,为了保证 比赛的公平性,将会从中抽取 10 万条作为训练集,5 万条作为测试集 A,5 万条作为测试集 B。同时会对名称、车辆类型、变速箱、model、燃油类型、品牌、公里数、价格等信息进行脱敏,处理异常值。
一般而言,对于数据在比赛界面都有对应的数据概况介绍(匿名特征除外),说明列的性质特征。了解列的性质会有助于我们对于数据的理解和后续分析。
Tip:匿名特征,就是未告知数据列所属的性质的特征列。
EDA一般步骤
1. 读取数据,清洗数据
目的:保证数据可供接下来的机器学习使用
缺失值,异常值,重复值,变量是否需要转换,是否需要抽样,是否需要增加新特征等。
缺失值处理:
(1)删除:当缺失值占比较大时,对后期贡献较小,直接删除即可(慎用)
(2)填补:缺失值占比较小且对后期贡献较大
- 可以用当前统计量的均值,中位数进行填充
- 可以用分组后的统计量均值,中位数进行填充
(3)删除具有缺失值的行,但是会删掉未缺失的其他列(不推荐使用)
异常值处理:
2.评测指标:
一般问题评价指标说明:
什么是评估指标:
评估指标即是我们对于一个模型效果的数值型量化。(有点类似与对于一个商品评价打分,而这是针对于模型效果和理想效果之间的一个打分)
一般来说分类和回归问题的评价指标有如下一些形式:
分类算法常见的评估指标如下:
- 对于二类分类器/分类算法,评价指标主要有accuracy, [Precision,Recall,F-score,Pr曲线],ROC-AUC曲线。
- 对于多类分类器/分类算法,评价指标主要有accuracy, [宏平均和微平均,F-score]。
对于回归预测类常见的评估指标如下:
- 平均绝对误差(Mean Absolute Error,MAE),均方误差(Mean Squared Error,MSE),平均绝对百分误差(Mean Absolute Percentage Error,MAPE),均方根误差(Root Mean Squared Error), R2(R-Square)
平均绝对误差 平均绝对误差(Mean Absolute Error,MAE):平均绝对误差,其能更好地反映预测值与真实值误差的实际情况,其计算公式如下:
均方误差 均方误差(Mean Squared Error,MSE),均方误差,其计算公式为:
R2(R-Square)的公式为: 残差平方和:
![]()
总平均值:
![]()
解题思路:
- 此题为传统的数据挖掘问题,通过数据科学以及机器学习深度学习的办法来进行建模得到结果。
- 此题是一个典型的回归问题。
- 主要应用xgb、lgb、catboost,以及pandas、numpy、matplotlib、seabon、sklearn、keras等等数据挖掘常用库或者框架来进行数据挖掘任务。
- 通过EDA来挖掘数据的联系和自我熟悉数据
数据从官网下载即可:
2.1分类指标评价计算示例
import pandas as pd
import numpy as np
path = './'
# 1) 载入训练集和测试集;
# Train_data = pd.read_csv(path+'car_train.csv', sep=' ')
# Test_data = pd.read_csv(path+'car_testB.csv', sep=' ')
Train_data = pd.read_csv('car_train.csv', sep=' ')
Test_data = pd.read_csv('car_testB.csv', sep=' ')
print('Train data shape:',Train_data.shape) #包含了标签所以多一列
print('TestA data shape:',Test_data.shape)Train data shape: (150000, 31) TestA data shape: (50000, 30)
from sklearn.metrics import accuracy_score
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 1]
print('ACC:',accuracy_score(y_true, y_pred))
ACC: 0.75## Precision,Recall,F1-score
from sklearn import metrics
y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]
print('Precision',metrics.precision_score(y_true, y_pred))
print('Recall',metrics.recall_score(y_true, y_pred))
print('F1-score:',metrics.f1_score(y_true, y_pred))
Precision 1.0
Recall 0.5
F1-score: 0.6666666666666666import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))
AUC socre: 0.752.2 回归指标评价计算示例
# coding=utf-8
import numpy as np
from sklearn import metrics
# MAPE需要自己实现
def mape(y_true, y_pred):
return np.mean(np.abs((y_pred - y_true) / y_true))
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
# MSE
print('MSE:',metrics.mean_squared_error(y_true, y_pred))
# RMSE
print('RMSE:',np.sqrt(metrics.mean_squared_error(y_true, y_pred)))
# MAE
print('MAE:',metrics.mean_absolute_error(y_true, y_pred))
# MAPE
print('MAPE:',mape(y_true, y_pred))MSE: 0.2871428571428571 RMSE: 0.5358571238146014 MAE: 0.4142857142857143 MAPE: 0.1461904761904762
## R2-score
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print('R2-score:',r2_score(y_true, y_pred))
R2-score: 0.94860813704496793.数据探索性分析(Exploratory Data Analysis,EDA)
3.1 导入函数工具箱
## 基础工具
import numpy as np
import pandas as pd
import warnings
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.special import jn
from IPython.display import display, clear_output
import time
warnings.filterwarnings('ignore')
%matplotlib inline
## 模型预测的
from sklearn import linear_model
from sklearn import preprocessing
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor
## 数据降维处理的
from sklearn.decomposition import PCA,FastICA,FactorAnalysis,SparsePCA
import lightgbm as lgb
import xgboost as xgb
## 参数搜索和评价的
from sklearn.model_selection import GridSearchCV,cross_val_score,StratifiedKFold,train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error#coding:utf-8
#导入warnings包,利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno没有得自行安装一下下相应的库如:
pip install lightgbm -i https://pypi.tuna.tsinghua.edu.cn/simple3.2 数据信息查看及描述性分析
3.2.1 简略观察数据信息(head()+shape):
## 通过Pandas对于数据进行读取 (pandas是一个很友好的数据读取函数库)
Train_data = pd.read_csv('car_train.csv', sep=' ')
Test_data = pd.read_csv('car_testB.csv', sep=' ')
## 输出数据的大小信息
print('Train data shape:',Train_data.shape) #包含了标签所以多一列
print('TestA data shape:',Test_data.shape)## 通过.head() 简要浏览读取数据的形式
Train_data.head()## 2) 简略观察数据(head()+shape)
Train_data.head().append(Train_data.tail())可以查看开始和结尾信息:
要养成看数据集的head()以及shape的习惯,这会让你每一步更放心,导致接下里的连串的错误, 如果对自己的pandas等操作不放心,建议执行一步看一下,这样会有效的方便你进行理解函数并进行操作
3.2.2 通过describe()来熟悉数据的相关统计量
describe种有每列的统计量,个数count、平均值mean、方差std、最小值min、中位数25% 50% 75% 、以及最大值 看这个信息主要是瞬间掌握数据的大概的范围以及每个值的异常值的判断,比如有的时候会发现999 9999 -1 等值这些其实都是nan的另外一种表达方式,有的时候需要注意下
## 通过 .describe() 可以查看数值特征列的一些统计信息
Train_data.describe()可以看出power功率和price交易价格的std标准差较大,price的最小值只有11元,说明离散程度较严重。seller和offtertype标准差极小,属于异常数据,后续处理。
查看异常值检测(上面有数据概览时提及过notRepairedDamage、power功率和price字段可能存在异常。)
3.2.3 通过info()来熟悉数据类型
info 通过info来了解数据每列的type,有助于了解是否存在除了nan以外的特殊符号异常
## 通过 .info() 简要可以看到对应一些数据列名,以及NAN缺失信息
Train_data.info()RangeIndex: 150000 entries, 0 to 149999 Data columns (total 31 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 SaleID 150000 non-null int64 1 name 150000 non-null int64 2 regDate 150000 non-null int64 3 model 149999 non-null float64 4 brand 150000 non-null int64 5 bodyType 145494 non-null float64 6 fuelType 141320 non-null float64 7 gearbox 144019 non-null float64 8 power 150000 non-null int64 9 kilometer 150000 non-null float64 10 notRepairedDamage 150000 non-null object 11 regionCode 150000 non-null int64 12 seller 150000 non-null int64 13 offerType 150000 non-null int64 14 creatDate 150000 non-null int64 15 price 150000 non-null int64 16 v_0 150000 non-null float64 17 v_1 150000 non-null float64 18 v_2 150000 non-null float64 19 v_3 150000 non-null float64 20 v_4 150000 non-null float64 21 v_5 150000 non-null float64 22 v_6 150000 non-null float64 23 v_7 150000 non-null float64 24 v_8 150000 non-null float64 25 v_9 150000 non-null float64 26 v_10 150000 non-null float64 27 v_11 150000 non-null float64 28 v_12 150000 non-null float64 29 v_13 150000 non-null float64 30 v_14 150000 non-null float64 dtypes: float64(20), int64(10), object(1) memory usage: 35.5+ MB
可以看出字段model车型编码、bodytype车身类型、fueltype燃油类型、gearbox变速箱均有缺失值,所有字段都是数值型,除了notRepairedDamage汽车尚有未修复的损坏,需要注意。v_0至v_14均为15个匿名特征。
可以发现除了notRepairedDamage 为object类型其他都为数字 这里我们把他的几个不同的值都进行显示就知道了
Train_data['notRepairedDamage'].value_counts()0.0 111361
- 24324
1.0 14315
Name: notRepairedDamage, dtype: int64可以看出来‘ - ’也为空缺值,因为很多模型对nan有直接的处理,这里我们先不做处理,先替换成nan(可以看出notRepairedDamage字段中有2.4w个-缺失,由于很多模型对缺失值都有处理,因此将-替换为nan)
Train_data['notRepairedDamage'].replace('-', np.nan, inplace=True)再看一下效果:
offerType和seller数据存在严重倾斜,对预测不会有什么帮助,因此删掉。
Train_data['notRepairedDamage'].value_counts()
0.0 111361
1.0 14315
Name: notRepairedDamage, dtype: int64以下两个类别特征严重倾斜,一般不会对预测有什么帮助,故这边先删掉,当然你也可以继续挖掘,但是一般意义不大 ;没什么特征删除即可
3.2.4 判断数据缺失和异常
## 1) 查看每列的存在nan情况
Train_data.isnull().sum()
SaleID 0
name 0
regDate 0
model 1
brand 0
bodyType 4506
fuelType 8680
gearbox 5981
power 0
kilometer 0
notRepairedDamage 0
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
dtype: int64# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar()通过以上两句可以很直观的了解哪些列存在 “nan”, 并可以把nan的个数打印,主要的目的在于 nan存在的个数是否真的很大,如果很小一般选择填充,如果使用lgb等树模型可以直接空缺,让树自己去优化,但如果nan存在的过多、可以考虑删掉
# 可视化看下缺省值
msno.matrix(Train_data.sample(250))msno.bar(Train_data.sample(1000))可视化有三列有缺省,notRepairedDamage缺省得最多。
通过上图可以直观的看到哪些字段存在缺失值,缺失数量是否庞大,如果较少可以填充,一般lgb等树模型可以空缺让模型自己处理,缺失值量较多则选择删除该字段。
3.2.5 了解预测值的分布
对预测值进行分析,也就是目标值。
Train_data['price']
0 1850
1 3600
2 6222
3 2400
4 5200
...
149995 5900
149996 9500
149997 7500
149998 4999
149999 4700
Name: price, Length: 150000, dtype: int64对预测值进行统计:
Train_data['price'].value_counts()
500 2337
1500 2158
1200 1922
1000 1850
2500 1821
...
25321 1
8886 1
8801 1
37920 1
8188 1
Name: price, Length: 3763, dtype: int64对分布情况进行验证:
## 1) 总体分布概况(无界约翰逊分布等)
import scipy.stats as st
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
plt.figure(2); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)可以看出价格不服从正态分布,所以在进行回归之前,它必须进行转换。虽然对数变换做得很好,但最佳拟合是无界约翰逊分布。
如分布图所示,price不符合正态分布在回归之前要做转换。虽然对数拟合做得很好但是最佳拟合还是johnsonsu。
Tips:sns.distplot可以做单变量的直方图,参数kde=True直接绘制密度曲线图,参数fit=传入scipy.stats中的分布类型,用于在观察变量上抽取相关统计特征来强行拟合指定的分布。既不定义kde也不定义fit,返回图表为直方图纵坐标表示的是频数。
## 2) 查看skewness 斜偏(偏度)and kurtosis峰度
sns.distplot(Train_data['price']);
print("Skewness: %f" % Train_data['price'].skew())
print("Kurtosis: %f" % Train_data['price'].kurt())#得到每个值的峰度和偏度
Train_data.skew(), Train_data.kurt()
(SaleID 6.017846e-17
name 5.576058e-01
regDate 2.849508e-02
model 1.484388e+00
.....
SaleID -1.200000
name -1.039945
regDate -0.697308
model 1.740483
brand 1.076201
bodyType 0.206937
fuelType 5.88004
....绘制各个数据峰度偏度图
sns.distplot(Train_data.skew(),color='blue',axlabel ='Skewness')
sns.distplot(Train_data.kurt(),color='orange',axlabel ='Kurtness')图上可以看出train中某些字段的偏度为-80和60+,峰度为6000,7000+,分别是power和creatdate。
正态分布的峰度和偏度均为0,price的偏度为3.35说明是右偏,尾部在右侧,右侧有极端值,偏度越大离群程度越高。峰度为19说明比正态分布更加陡峭属于尖峰,峰度越大数据中极端值越多。
skew、kurt说明参考数据的偏度和峰度——df.skew()、df.kurt() - 喜欢吃面的猪猪 - 博客园
## 3) 查看预测值的具体频数
plt.hist(Train_data['price'], orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()查看频数, 大于20000得值极少,其实这里也可以把这些当作特殊得值(异常值)直接用填充或者删掉,再前面进行,
可以看出price的均值为5923,标准差为7501,最大值有99999,回归最怕离群点
price与正态分布相差甚远,远处离群点数量较多,训练出的误差较大,无法准确预测,正常来说可以去掉。
可以看出大于20000价格的数量很少,可以当做异常值填充。
将price进行log变换后趋近于正态分布,可以用来预测。
# log变换 z之后的分布较均匀,可以进行log变换进行预测,这也是预测问题常用的trick
plt.hist(np.log(Train_data['price']), orientation = 'vertical',histtype = 'bar', color ='red')
plt.show()3.2.6 特征分为类别特征和数字特征,并对类别特征查看unique分布
数据类型--列
- name - 汽车编码
- regDate - 汽车注册时间
- model - 车型编码
- brand - 品牌
- bodyType - 车身类型
- fuelType - 燃油类型
- gearbox - 变速箱
- power - 汽车功率
- kilometer - 汽车行驶公里
- notRepairedDamage - 汽车有尚未修复的损坏
- regionCode - 看车地区编码
- seller - 销售方 【以删】
- offerType - 报价类型 【以删】
- creatDate - 广告发布时间
- price - 汽车价格
- v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14'(根据汽车的评论、标签等大量信息得到的embedding向量)【人工构造 匿名特征
# 分离label即预测值
Y_train = Train_data['price']
# 这个区别方式适用于没有直接label coding的数据
# 这里不适用,需要人为根据实际含义来区分
# 数字特征
# numeric_features = Train_data.select_dtypes(include=[np.number])
# numeric_features.columns
# # 类型特征
# categorical_features = Train_data.select_dtypes(include=[np.object])
# categorical_features.columns
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]
# 特征nunique分布
for cat_fea in categorical_features:
print(cat_fea + "的特征分布如下:")
print("{}特征有个{}不同的值".format(cat_fea, Train_data[cat_fea].nunique()))
print(Train_data[cat_fea].value_counts())部分效果如下:
name的特征分布如下:
name特征有个99662不同的值
708 282
387 282
55 280
1541 263
203 233
...
5074 1
7123 1
11221 1
13270 1
174485 1
Name: name, Length: 99662, dtype: int643.2.7 数字特征分析!!
numeric_features.append('price')
numeric_features
['power',
'kilometer',
'v_0',
'v_1',
'v_2',
'v_3',
'v_4',
'v_5',
'v_6',
'v_7',
'v_8',
'v_9',
'v_10',
'v_11',
'v_12',
'v_13',
'v_14',
'price']
Train_data.head()数值特征和预测价格的相关性分析:
![]()
定序变量:比如消费能力:【1,5】之类的。
![]()
## 1) 相关性分析
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'\n')price 1.000000
v_12 0.692823
v_8 0.685798
v_0 0.628397
power 0.219834
v_5 0.164317
v_2 0.085322
v_6 0.068970
v_1 0.060914
v_14 0.035911
v_13 -0.013993
v_7 -0.053024
v_4 -0.147085
v_9 -0.206205
v_10 -0.246175
v_11 -0.275320
kilometer -0.440519
v_3 -0.730946
Name: price, dtype: float64 画热力图:
皮尔逊相关系数
f , ax = plt.subplots(figsize = (7, 7)) #设置图片大小
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True, vmax=0.8) #参数设置
sns.heatmap(correlation,square = True,annot=True ,vmax=0.8) #显示数值seaborn.heatmap参数介绍:seaborn.heatmap参数介绍_liff_lee的博客-CSDN博客_sns.heatmap参数
vo和v5 v6和v1相关性很高,不符合各个特征之间是相互独立的,会产生负贡献问题,这时候就要剔除某一个特征。
图中最右侧是颜色代表的相关系数值,price与v_0、v_8、v_12相关性较高,v_11和v_2、v_7,v_12和v_8,v_13和v_9相关系数都很高。
进行偏度和峰度分析:
del price_numeric['price']
## 2) 查看几个特征得 偏度和峰值
for col in numeric_features:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(Train_data[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())
)power Skewness: 65.86 Kurtosis: 5733.45
kilometer Skewness: -1.53 Kurtosis: 001.14
v_0 Skewness: -1.32 Kurtosis: 003.99
v_1 Skewness: 00.36 Kurtosis: -01.75
v_2 Skewness: 04.84 Kurtosis: 023.86
v_3 Skewness: 00.11 Kurtosis: -00.42
v_4 Skewness: 00.37 Kurtosis: -00.20
v_5 Skewness: -4.74 Kurtosis: 022.93
v_6 Skewness: 00.37 Kurtosis: -01.74
v_7 Skewness: 05.13 Kurtosis: 025.85
v_8 Skewness: 00.20 Kurtosis: -00.64
v_9 Skewness: 00.42 Kurtosis: -00.32
v_10 Skewness: 00.03 Kurtosis: -00.58
v_11 Skewness: 03.03 Kurtosis: 012.57
v_12 Skewness: 00.37 Kurtosis: 000.27
v_13 Skewness: 00.27 Kurtosis: -00.44
v_14 Skewness: -1.19 Kurtosis: 002.39
price Skewness: 03.35 Kurtosis: 019.00可以看到power有问题的,需要处理一下。
可见power,v_2,v_5,v_7,v_11,price的峰度和偏度都有异常。
每个数字特征得分布可视化;进行可视化,部分效果如下:
## 3) 每个数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")可以看出匿名特征相对分布均匀。
数字特征相互之间的关系可视化【程序跑得很慢】
## 4) 数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()可以明显看出,v_1和v_6呈明显线性关系。
此处是多变量之间的关系可视化,可视化更多学习可参考很不错的文章,值得点。
Seaborn-05-Pairplot多变量图 - 简书
多变量互相回归关系可视化
## 5) 多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)3.2.8 类别特征分析(箱图,小提琴图,柱形图)
- unique分布
## 1) unique分布
for fea in categorical_features:
print(Train_data[fea].nunique())99662 248 40 8 7 2 2 7905
categorical_features['name',
'model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage',
'regionCode']- 类别特征箱形图可视化
## 2) 类别特征箱形图可视化
# 因为 name和 regionCode的类别太稀疏了,这里我们把不稀疏的几类画一下
categorical_features = ['model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage']
for c in categorical_features:
Train_data[c] = Train_data[c].astype('category')
if Train_data[c].isnull().any():
Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
Train_data[c] = Train_data[c].fillna('MISSING')
def boxplot(x, y, **kwargs):
sns.boxplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features) #预测值
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")any() 函数:Python any() 函数 | 菜鸟教程
any() 函数用于判断给定的可迭代参数 iterable 是否全部为 False,则返回 False,如果有一个为 True,则返回 True。
元素除了是 0、空、FALSE 外都算 TRUE。
缺失值处理链接:5.1 缺失值处理isnull、.dropna()、fillna()、 - 简书
fillna缺失值填充,缺失值填充为missing
具体箱图参数以及图形设置参考下面博客:
**boxplot用法 python_【Python可视化3】Seaborn之箱线图与小提琴图
可以看出brand=24和37的车型价格区间较高离散程度较大,价位较低的离散程度较小;bodytype=6商务车价位稍高;混合动力和柴油的车价位稍高;自动挡汽车价位稍高。这些都可以作为特征在特征工程中使用。
- 类别特征的小提琴图可视化
![]()
## 3) 类别特征的小提琴图可视化
catg_list = categorical_features
target = 'price'
for catg in catg_list :
sns.violinplot(x=catg, y=target, data=Train_data)
plt.show()具体图参数以及图形设置参考下面博客:
**boxplot用法 python_【Python可视化3】Seaborn之箱线图与小提琴图
categorical_features = ['model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage']- 类别特征的柱形图可视化
## 4) 类别特征的柱形图可视化
def bar_plot(x, y, **kwargs):
sns.barplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(bar_plot, "value", "price")这里的barplot默认计算平均值,因此能看出brand=24的车型均值在3w元,brand=34车型均值价位最低;商务车价位最高微型车价位最低;电动、混合动、柴油车价位偏高,液化石油气价位最低;
- 类别特征的每个类别频数可视化(count_plot)
## 5) 类别特征的每个类别频数可视化(count_plot)
def count_plot(x, **kwargs):
sns.countplot(x=x)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data, value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")如何一幅一幅生成图片:
把特征一个一个输入即可:
def count_plot(x, **kwargs):
sns.countplot(x=x)
x=plt.xticks(rotation=90)
catg_list=categorical_features
for catg in catg_list :
f = pd.melt(Train_data, value_vars=catg )
g = sns.FacetGrid(f, col="variable", col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")3.3 用pandas_profiling生成数据报告
pip install pandas_profiling -i https://pypi.tuna.tsinghua.edu.cn/simplepfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")3.4 特征与标签构建
- 提取数值类型特征列名
numerical_cols = Train_data.select_dtypes(exclude = 'object').columns
print(numerical_cols)
Index(['SaleID', 'name', 'regDate', 'model', 'brand', 'bodyType', 'fuelType',
'gearbox', 'power', 'kilometer', 'regionCode', 'seller', 'offerType',
'creatDate', 'price', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6',
'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13', 'v_14'],
dtype='object')
categorical_cols = Train_data.select_dtypes(include = 'object').columns
print(categorical_cols)
Index(['notRepairedDamage'], dtype='object')- 构建训练和测试样本
## 选择特征列
feature_cols = [col for col in numerical_cols if col not in ['SaleID','name','regDate','creatDate','price','model','brand','regionCode','seller']]
feature_cols = [col for col in feature_cols if 'Type' not in col]
## 提前特征列,标签列构造训练样本和测试样本
X_data = Train_data[feature_cols]
Y_data = Train_data['price']
X_test = Test_data[feature_cols]
print('X train shape:',X_data.shape)
print('X test shape:',X_test.shape)
X train shape: (150000, 18)
X test shape: (50000, 18)## 定义了一个统计函数,方便后续信息统计
def Sta_inf(data):
print('_min',np.min(data))
print('_max:',np.max(data))
print('_mean',np.mean(data))
print('_ptp',np.ptp(data))
print('_std',np.std(data))
print('_var',np.var(data))- 统计标签的基本分布信息
print('Sta of label:')
Sta_inf(Y_data)Sta of label: _min 11 _max: 99999 _mean 5923.327333333334 _ptp 99988 _std 7501.973469876635 _var 56279605.942732885
## 绘制标签的统计图,查看标签分布
plt.hist(Y_data)
plt.show()
plt.close()- 缺省值用-1填补
X_data = X_data.fillna(-1)
X_test = X_test.fillna(-1)4.模型训练与预测
4.1 利用xgb进行五折交叉验证查看模型的参数效果
## xgb-Model
xgr = xgb.XGBRegressor(n_estimators=120, learning_rate=0.1, gamma=0, subsample=0.8,\
colsample_bytree=0.9, max_depth=7) #,objective ='reg:squarederror'
#簇120,学习率0.1 ,深度为7
scores_train = []
scores = []
## 5折交叉验证方式,防止过拟合
sk=StratifiedKFold(n_splits=5,shuffle=True,random_state=0)
for train_ind,val_ind in sk.split(X_data,Y_data):
train_x=X_data.iloc[train_ind].values
train_y=Y_data.iloc[train_ind]
val_x=X_data.iloc[val_ind].values
val_y=Y_data.iloc[val_ind]
xgr.fit(train_x,train_y)
pred_train_xgb=xgr.predict(train_x)
pred_xgb=xgr.predict(val_x)
score_train = mean_absolute_error(train_y,pred_train_xgb)
scores_train.append(score_train)
score = mean_absolute_error(val_y,pred_xgb)
scores.append(score)
print('Train mae:',np.mean(score_train))
print('Val mae',np.mean(scores))得到结果:
Train mae: 622.836567743063 Val mae 714.0856746034109
以三折交叉验证为例:
先把数据分为三块,然后分别用任意两块得到第三块数据的预测值(或误差),然后取一个平均
五折的话可以说全部样本集都做了训练也都做了验证。
手动调参一下值:然后比较mae是否会下降,尤其是验证集上的值。
## xgb-Model
xgr = xgb.XGBRegressor(n_estimators=120, learning_rate=0.1, gamma=0, subsample=0.8,\
colsample_bytree=0.9, max_depth=7) #,objective ='reg:squarederror'
learning_rate=0.1
subsample=0.8
max_depth=7
n_estimators=1204.2 定义xgb和lgb模型函数
def build_model_xgb(x_train,y_train):
model = xgb.XGBRegressor(n_estimators=150, learning_rate=0.1, gamma=0, subsample=0.8,\
colsample_bytree=0.9, max_depth=7) #, objective ='reg:squarederror'
model.fit(x_train, y_train)
return model
def build_model_lgb(x_train,y_train):
estimator = lgb.LGBMRegressor(num_leaves=127,n_estimators = 150)
param_grid = {
'learning_rate': [0.01, 0.05, 0.1, 0.2],
}
gbm = GridSearchCV(estimator, param_grid) #网格搜索
gbm.fit(x_train, y_train)
return gbm网格搜索自动调参方式,对param_grid中参数进行改正,可以添加学习率等等参数
param_grid = {
'learning_rate': [0.01, 0.05, 0.1, 0.2],
'n_estimators': [100, 140, 120, 130],
}这里就有4*4--16中可能,选出交叉验证效果最好的。
4.3 切分数据集(Train,Val)进行模型训练,评价和预测
## Split data with val
x_train,x_val,y_train,y_val = train_test_split(X_data,Y_data,test_size=0.3)按比例切分,也可以4:1 即test_size=0.2
print('Train lgb...')
model_lgb = build_model_lgb(x_train,y_train)
val_lgb = model_lgb.predict(x_val)
MAE_lgb = mean_absolute_error(y_val,val_lgb)
print('MAE of val with lgb:',MAE_lgb)
print('Predict lgb...')
model_lgb_pre = build_model_lgb(X_data,Y_data)
subA_lgb = model_lgb_pre.predict(X_test)
print('Sta of Predict lgb:')
Sta_inf(subA_lgb)Train lgb...
MAE of val with lgb: 690.0018296768471
Predict lgb...
Sta of Predict lgb:
_min -589.8793550785414
_max: 90760.26063584947
_mean 5906.935218383807
_ptp 91350.13999092802
_std 7344.644970956768
_var 53943809.749400534print('Train xgb...')
model_xgb = build_model_xgb(x_train,y_train)
val_xgb = model_xgb.predict(x_val)
MAE_xgb = mean_absolute_error(y_val,val_xgb)
print('MAE of val with xgb:',MAE_xgb)
print('Predict xgb...')
model_xgb_pre = build_model_xgb(X_data,Y_data)
subA_xgb = model_xgb_pre.predict(X_test)
print('Sta of Predict xgb:')
Sta_inf(subA_xgb)Train xgb...
MAE of val with xgb: 708.597995025762
Predict xgb...
Sta of Predict xgb:
_min -318.20892
_max: 90140.625
_mean 5910.7607
_ptp 90458.836
_std 7345.965
_var 53963196.0可以看到预测结果:最小值为负值,价格应该为证,导致这个情况就是一些异常值存在,应该剔除。
4.4 进行两模型的结果加权融合
## 这里我们采取了简单的加权融合的方式
val_Weighted = (1-MAE_lgb/(MAE_xgb+MAE_lgb))*val_lgb+(1-MAE_xgb/(MAE_xgb+MAE_lgb))*val_xgb
val_Weighted[val_Weighted<0]=10 # 由于我们发现预测的最小值有负数,而真实情况下,price为负是不存在的,由此我们进行对应的后修正
print('MAE of val with Weighted ensemble:',mean_absolute_error(y_val,val_Weighted))权重赋值:看两个模型的MAE,误差大的权重小,误差小的权重大点。
MAE of val with Weighted ensemble: 684.2134943041136比上述下降一些。
sub_Weighted = (1-MAE_lgb/(MAE_xgb+MAE_lgb))*subA_lgb+(1-MAE_xgb/(MAE_xgb+MAE_lgb))*subA_xgb
## 查看预测值的统计进行
plt.hist(Y_data)
plt.show()
plt.close()sub = pd.DataFrame()
sub['SaleID'] = TestA_data.SaleID
sub['price'] = sub_Weighted
sub.to_csv('./sub_Weighted.csv',index=False)
sub.head()| SaleID | price | |
|---|---|---|
| 0 | 200000 | 1177.295593 |
| 1 | 200001 | 1807.105761 |
| 2 | 200002 | 8560.957073 |
| 3 | 200003 | 1346.563319 |
| 4 | 200004 | 2074.186172 |
5. 经验总结
码源
本项目码源链接:https://www.heywhale.com/mw/project/64367e0a2a3d6dc93d22054f
机器学习码源专栏链接:https://www.heywhale.com/home/column/64141d6b1c8c8b518ba97dcc
所给出的EDA步骤为广为普遍的步骤,在实际的不管是工程还是比赛过程中,这只是最开始的一步,也是最基本的一步。
接下来一般要结合模型的效果以及特征工程等来分析数据的实际建模情况,根据自己的一些理解,查阅文献,对实际问题做出判断和深入的理解。
最后不断进行EDA与数据处理和挖掘,来到达更好的数据结构和分布以及较为强势相关的特征
数据探索在机器学习中我们一般称为EDA(Exploratory Data Analysis):
是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索,通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。
数据探索有利于我们发现数据的一些特性,数据之间的关联性,对于后续的特征构建是很有帮助的。
-
对于数据的初步分析(直接查看数据,或.sum(), .mean(),.descirbe()等统计函数)可以从:样本数量,训练集数量,是否有时间特征,是否是时许问题,特征所表示的含义(非匿名特征),特征类型(字符类似,int,float,time),特征的缺失情况(注意缺失的在数据中的表现形式,有些是空的有些是”NAN”符号等),特征的均值方差情况。
-
分析记录某些特征值缺失占比30%以上样本的缺失处理,有助于后续的模型验证和调节,分析特征应该是填充(填充方式是什么,均值填充,0填充,众数填充等),还是舍去,还是先做样本分类用不同的特征模型去预测。
-
对于异常值做专门的分析,分析特征异常的label是否为异常值(或者偏离均值较远或者事特殊符号),异常值是否应该剔除,还是用正常值填充,是记录异常,还是机器本身异常等。
-
对于Label做专门的分析,分析标签的分布情况等。
-
进步分析可以通过对特征作图,特征和label联合做图(统计图,离散图),直观了解特征的分布情况,通过这一步也可以发现数据之中的一些异常值等,通过箱型图分析一些特征值的偏离情况,对于特征和特征联合作图,对于特征和label联合作图,分析其中的一些关联性。
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第2张图片](http://img.e-com-net.com/image/info8/1c8741605e4e4ccab4db30b2588b8803.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第3张图片](http://img.e-com-net.com/image/info8/c04a2fb56bec4109be160f803fb86154.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第4张图片](http://img.e-com-net.com/image/info8/54bf0923eded42749b54a162854298b5.jpg)
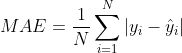
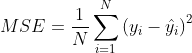
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第5张图片](http://img.e-com-net.com/image/info8/f738c27401cd43178db30ebe47212178.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第6张图片](http://img.e-com-net.com/image/info8/7fbc6cd4812c4768a61c5730e18dbb46.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第7张图片](http://img.e-com-net.com/image/info8/eb16f80bcbcd4f2eb45f86046afbdb51.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第8张图片](http://img.e-com-net.com/image/info8/74a61e791ac747beadca83f467d67573.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第9张图片](http://img.e-com-net.com/image/info8/6f916ccbaada46049feba0804566f825.png)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第10张图片](http://img.e-com-net.com/image/info8/65de1011ad534109a2f99fba4b5de8f0.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第11张图片](http://img.e-com-net.com/image/info8/ca3a2cdc6dd146fc820ee7d5e9ed92d2.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第12张图片](http://img.e-com-net.com/image/info8/374a5c6903bd472691329103c2ab183b.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第13张图片](http://img.e-com-net.com/image/info8/6ee1bbc2991f4f7d8051f01b2f0c6aaa.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第14张图片](http://img.e-com-net.com/image/info8/fb673780dfc3471ead30ad4faced3424.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第15张图片](http://img.e-com-net.com/image/info8/0980cb825dda4206a5826bdc3392124c.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第16张图片](http://img.e-com-net.com/image/info8/5ed54544b5c3455cb74b6ee0d256397b.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第17张图片](http://img.e-com-net.com/image/info8/0c95a1eb839f41458f01bec752b98c78.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第18张图片](http://img.e-com-net.com/image/info8/9fa768044c0d4d4cb54a72deffb16406.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第19张图片](http://img.e-com-net.com/image/info8/ff5b1b977f55448492a690783fde78e8.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第20张图片](http://img.e-com-net.com/image/info8/1c6ff1b3aa164a6aa5db3466a07a0991.jpg)

![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第21张图片](http://img.e-com-net.com/image/info8/2938440b1475438fb191623477cc172a.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第22张图片](http://img.e-com-net.com/image/info8/5f8f5aa05cf940619d596629967f68ed.png)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第23张图片](http://img.e-com-net.com/image/info8/78b8d60c9d594c5b94df05a503688a2d.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第24张图片](http://img.e-com-net.com/image/info8/c5c51ae2953b42578d0f2d2e4fd917b9.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第25张图片](http://img.e-com-net.com/image/info8/90b895c2241e4e8ab6577c54e1f45df0.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第26张图片](http://img.e-com-net.com/image/info8/8ad54a262c2243b692d29504c5fa0414.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第27张图片](http://img.e-com-net.com/image/info8/11112d537083431b91d74da217406d19.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第28张图片](http://img.e-com-net.com/image/info8/12c0587713124767af1b649595f36cb7.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第29张图片](http://img.e-com-net.com/image/info8/7edafe93588d4e8fb4ab8fda449479f6.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第30张图片](http://img.e-com-net.com/image/info8/3fe8b44474174709b1ee36fb2330060e.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第31张图片](http://img.e-com-net.com/image/info8/375439631b7f4e5585541a2f045826af.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第32张图片](http://img.e-com-net.com/image/info8/8e922465e3c54a20a16bfebef5f97132.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第33张图片](http://img.e-com-net.com/image/info8/eb066f7760844dc495b80bf538bbb559.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第34张图片](http://img.e-com-net.com/image/info8/450b2fc538e5470990791796ab201b47.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第35张图片](http://img.e-com-net.com/image/info8/0639d03e23464194a709b2572f0a73d9.jpg)
![B.数据挖掘[一]---汽车车交易价格预测(测评指标;EDA)_第36张图片](http://img.e-com-net.com/image/info8/3fe1e697a49d46a3b06f686d0571fc2c.jpg)