5.图论(0x3f:从周赛中学算法 2022下)
来自0x3f【从周赛中学算法 - 2022 年周赛题目总结(下篇)】:https://leetcode.cn/circle/discuss/WR1MJP/
周赛中的图论题目比较少,除了下面选的 DFS、BFS、拓扑排序、基环树、二分图判定等,还有最短路、DFS 时间戳等(这些可以在上半年的周赛题目中学到)。
注:偶见于周赛第三题(约占 10%)和第四题(约占 13%)。
| 题目 | 难度 | 备注 |
|---|---|---|
| 2368. 受限条件下可到达节点的数目 | 1477 | DFS/BFS 典型题 |
| 2385. 感染二叉树需要的总时间 | 1711 | DFS+BFS |
| 2359. 找到离给定两个节点最近的节点 | 1715 | |
| 2360. 图中的最长环 | 1897 | 内向基环树+时间戳技巧 |
| 2509. 查询树中环的长度 | 1948 | 最近公共祖先 |
| 2392. 给定条件下构造矩阵 | 1961 | 拓扑排序 |
| 2467. 树上最大得分和路径 | 2053 | |
| 2493. 将节点分成尽可能多的组 | 2415 | 二分图判定(可选)+BFS |
文章目录
- 灵神-从周赛中学算法(图论)
-
- [2368. 受限条件下可到达节点的数目](https://leetcode.cn/problems/reachable-nodes-with-restrictions/)
- [2385. 感染二叉树需要的总时间](https://leetcode.cn/problems/amount-of-time-for-binary-tree-to-be-infected/)
- [2359. 找到离给定两个节点最近的节点](https://leetcode.cn/problems/find-closest-node-to-given-two-nodes/)+进阶问题
- [2360. 图中的最长环](https://leetcode.cn/problems/longest-cycle-in-a-graph/)
- [2509. 查询树中环的长度](https://leetcode.cn/problems/cycle-length-queries-in-a-tree/)
- [2392. 给定条件下构造矩阵](https://leetcode.cn/problems/build-a-matrix-with-conditions/)
- [2467. 树上最大得分和路径](https://leetcode.cn/problems/most-profitable-path-in-a-tree/)
- [2493. 将节点分成尽可能多的组](https://leetcode.cn/problems/divide-nodes-into-the-maximum-number-of-groups/)
灵神-从周赛中学算法(图论)
2368. 受限条件下可到达节点的数目
难度中等28
现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 ,共有 n - 1 条边。
给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。
在不访问受限节点的前提下,返回你可以从节点 0 到达的 最多 节点数目*。*
注意,节点 0 不 会标记为受限节点。
示例 1:
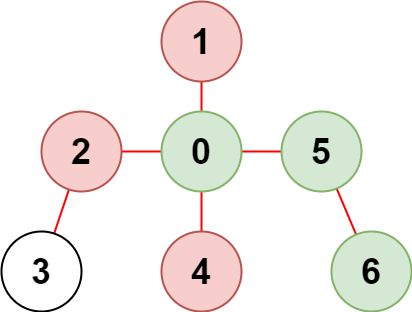
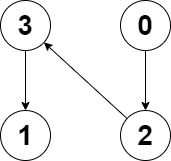
输入:n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出:4
解释:上图所示正是这棵树。
在不访问受限节点的前提下,只有节点 [0,1,2,3] 可以从节点 0 到达。
示例 2:
输入:n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出:3
解释:上图所示正是这棵树。
在不访问受限节点的前提下,只有节点 [0,5,6] 可以从节点 0 到达。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树1 <= restricted.length < n1 <= restricted[i] < nrestricted中的所有值 互不相同
DFS
class Solution {
List<Integer>[] g;
Set<Integer> set;
int res = 0;
public int reachableNodes(int n, int[][] edges, int[] restricted) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for(int[] e : edges){
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x);
}
set = new HashSet<>();
for(int r : restricted) set.add(r);
dfs(0, -1);
return res;
}
public void dfs(int x, int fa){
res++;
for(int y : g[x]){
if(y != fa && !set.contains(y)){
dfs(y, x);
}
}
}
}
BFS
class Solution {
List<Integer>[] g;
Set<Integer> set;
int res = 0;
public int reachableNodes(int n, int[][] edges, int[] restricted) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for(int[] e : edges){
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x);
}
set = new HashSet<>();
for(int r : restricted) set.add(r);
boolean[] vis = new boolean[n];
Deque<Integer> dq = new ArrayDeque<>();
dq.addLast(0);
while(!dq.isEmpty()){
int x = dq.pollFirst();
vis[x] = true;
res++;
for(int y : g[x]){
if(!vis[y] && !set.contains(y)){
dq.addLast(y);
}
}
}
return res;
}
}
2385. 感染二叉树需要的总时间
难度中等37
给你一棵二叉树的根节点 root ,二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟,感染 将会从值为 start 的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
- 节点此前还没有感染。
- 节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数*。*
示例 1:
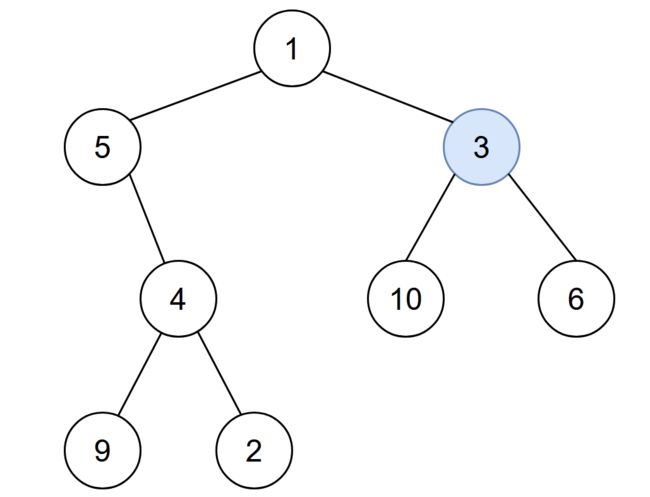
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2
感染整棵树需要 4 分钟,所以返回 4 。
示例 2:
输入:root = [1], start = 1
输出:0
解释:第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。
提示:
- 树中节点的数目在范围
[1, 105]内 1 <= Node.val <= 105- 每个节点的值 互不相同
- 树中必定存在值为
start的节点
题解:
DFS将二叉树转成图(Map表示的邻接矩阵),BFS遍历计算层深度
class Solution {
Map<Integer, List<Integer>> g;
public int amountOfTime(TreeNode root, int start) {
g = new HashMap<>();
dfs(root); // DFS 将二叉树转成图(Map表示的邻接矩阵)
int res = -1;
Set<Integer> vis = new HashSet<>();
Deque<Integer> dq = new ArrayDeque<>();
dq.addLast(start);
vis.add(start);
while(!dq.isEmpty()){
int size = dq.size();
while(size-- > 0){
int x = dq.pollFirst();
for(int y : g.get(x)){
if(!vis.contains(y)){
vis.add(y);
dq.addLast(y);
}
}
}
res++;
}
return res;
}
public void dfs(TreeNode root){
int x = root.val;
if(!g.containsKey(x)) g.put(x, new ArrayList<>());
if(root.left != null){
int y = root.left.val;
g.get(x).add(y);
if(!g.containsKey(y)) g.put(y, new ArrayList<>());
g.get(y).add(x);
dfs(root.left);
}
if(root.right != null){
int y = root.right.val;
g.get(x).add(y);
if(!g.containsKey(y)) g.put(y, new ArrayList<>());
g.get(y).add(x);
dfs(root.right);
}
}
}
2359. 找到离给定两个节点最近的节点+进阶问题
难度中等20
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
示例 1:
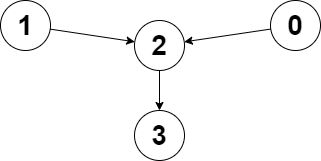
输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
示例 2:
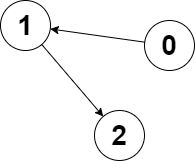
输入:edges = [1,2,-1], node1 = 0, node2 = 2
输出:2
解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
https://leetcode.cn/problems/find-closest-node-to-given-two-nodes/solution/by-lfool-t4y7/
首先看到这个题目,可以想到求出 node1 和 node2 到其它所有点的最短距离,然后遍历可选择的「中间点」。所以现在的问题就是如何求出其它点到起点的最短路径
「最短路径」算法有 最短路径-Dijkstra 和 无权值最短路径算法(BFS)
「Dijkstra」适用于加权有向图,没有负权重边,且无环,一般是求起点到其它所有点的最短路径,也可以改进为求两点的最短路径
「无权值最短路径算法(BFS)」适用于无权有向图,可以有环,一般是求两点的最短路径,也可以改进为求起点到其它所有点的最短路径
对于本题,每条边的权重均为 1,所以可以看作为无权值,我们使用上述的第二种方法「无权值最短路径算法(BFS)」
由于点与点之间最多只有一条边,所以可以简化「无权值最短路径算法(BFS)」
我的【丑陋】解法:从两个节点开始分别BFS(双BFS)
class Solution {
public int closestMeetingNode(int[] edges, int node1, int node2) {
if(node1 == node2) return node2;
int n = edges.length;
List<Integer>[] g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for(int i = 0; i < n; i++){
if(edges[i] == -1) continue;
g[i].add(edges[i]);
}
Set<Integer> set1 = new HashSet<>();
Set<Integer> set2 = new HashSet<>();
Deque<Integer> dq1 = new ArrayDeque<>();
Deque<Integer> dq2 = new ArrayDeque<>();
int len1 = 0, len2 = 0, res = Integer.MAX_VALUE;
set1.add(node1); set2.add(node2);
dq1.add(node1); dq2.add(node2);
while((!dq1.isEmpty() || !dq2.isEmpty()) && res == Integer.MAX_VALUE){
if(!dq1.isEmpty()){
len1++;
int size = dq1.size();
while(size-- > 0){
int x = dq1.pollFirst();
for(int y : g[x]){
if(!set1.contains(y)){
set1.add(y);
dq1.addLast(y);
}
if(set2.contains(y)){
res = Math.min(res, y);
}
}
}
}
if(!dq2.isEmpty()){
len2++;
int size = dq2.size();
while(size-- > 0){
int x = dq2.pollFirst();
for(int y : g[x]){
if(!set2.contains(y)){
set2.add(y);
dq2.addLast(y);
}
if(set1.contains(y)){
res = Math.min(res, y);
}
}
}
}
}
return res == Integer.MAX_VALUE ? -1 : res;
}
}
优雅解法:BFS计算到每个点的距离
https://leetcode.cn/problems/find-closest-node-to-given-two-nodes/solution/ji-suan-dao-mei-ge-dian-de-ju-chi-python-gr2u/
求出 node1 到每个点的距离 d1 和 node2 到每个点的距离 d2 (无法到达时设为一个比较大的数) ,然后遍历 d1 和 d2,答案即为max(d1[i],d2[i]) 的最小值所对应的 。若没有这样的节点,答案为 -1
- 这可以用 BFS 来做,但由于题目的输入是内向基环树 (森林),每个连通块至多有一个环,利用这一特性,代码实现时可以用一个简单的循环求出距离数组
class Solution {
// 本题利用了基环树的特点来简化求最短路的代码,也可以用普通的BFS求最短路
public int closestMeetingNode(int[] edges, int node1, int node2) {
// 把node1和node2到所有点的距离求出来 d
int[] d1 = calcDis(edges, node1);
int[] d2 = calcDis(edges, node2);
int n = edges.length;
int res = -1, mindis = n;
for(int i = 0; i < n; i++){
int d = Math.max(d1[i], d2[i]);
if(d < mindis){
mindis = d;
res = i;
}
}
return res;
}
public int[] calcDis(int[] edges, int x){
int n = edges.length;
int[] dis = new int[n];
Arrays.fill(dis, n); // 初始化路径不可达
int d = 0;
while(x >= 0 && dis[x] == n){
dis[x] = d++; // 如果有环一定会回到 x 上
x = edges[x];
}
return dis;
}
}
思考题
1.如果输入的不止两个节点 node1 和 node2,而是一个很长的nodes 列表,要怎么做呢?
2.如果输入的是 queries 询问数组,每个询问包含两个节点 node1和 node2 ,要你回答 closestMeetingNode(edges,node1,node2)的答案,要怎么做呢?
思考题答案:
如果都在树上:LCA最近公共祖先问题
如果都在基环上:二分答案,转换成若干区间是否有交集
如果是树 ==> 两个节点的最近公共祖先LCA问题
如果有基环 ==> A->B,答案是B
2360. 图中的最长环
难度困难30
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
示例 2:
输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
基环树朴素解法:
class Solution {
List<Integer>[] rg; // g的反图
int[] degree; // g上每个节点的入度
public int longestCycle(int[] edges) {
int n = edges.length;
rg = new ArrayList[n];
Arrays.setAll(rg, e -> new ArrayList<>());
degree = new int[n];
for(int v = 0; v < n; v++){
int w = edges[v];
if(w == -1) continue;
rg[w].add(v);
degree[w]++;
}
// 剪掉g上的所有树枝
Deque<Integer> dq = new ArrayDeque<>();
for(int i = 0; i < n; i++){
if(degree[i] == 0) dq.addLast(i);
}
while(!dq.isEmpty()){
int v = dq.pollFirst();
int w = edges[v];
if(w == -1) continue;
if(--degree[w] == 0) dq.addLast(w);
}
// 找到最大的基环
int maxRingSize = -1;
for(int i = 0; i < n; i++){
if(degree[i] <= 0) continue;
degree[i] = -1;
int ringsize = 1;
for(int v = edges[i]; v != i; v = edges[v]){//环循环终止条件v!= i,即转一圈
degree[v] = -1;
ringsize++;
}
maxRingSize = Math.max(maxRingSize, ringsize);
}
return maxRingSize;
}
}
利用时间戳简单实现
class Solution {
// 利用时间戳来实现找环的逻辑
// 初始时间戳clock=1,首次访问一个点x时,记录当前当问这个点的时间time[x]= clock,然后clock+1
// 如果找到了一个之前访问过的点x,且之前访问x的时间不早于starttime,说明找到了一个新的环
// 环长就是两次访问x的时间差,clock - time[x]
public int longestCycle(int[] edges) {
int n = edges.length, ans = -1;
var time = new int[n];
for (int i = 0, clock = 1; i < n; ++i) {
if (time[i] > 0) continue; // 访问过了
int x = i, startTime = clock;
while (x >= 0) {
if (time[x] > 0) { // 重复访问
//判断是找到了一个环,还是访问了一个之前找环过程中访问的点
if (time[x] >= startTime) // 找到了一个新的环
ans = Math.max(ans, clock - time[x]);
break;
}
time[x] = clock++;
x = edges[x];
}
}
return ans;
}
}
拓展问题:如果要输出环上所有的点,要怎么做?
- 从找到新环处重新跑一边
class Solution {
// 利用时间戳来实现找环的逻辑
// 初始时间戳clock=1,首次访问一个点x时,记录当前当问这个点的时间time[x]= clock,然后clock+1
// 如果找到了一个之前访问过的点x,且之前访问x的时间不早于starttime,说明找到了一个新的环
// 环长就是两次访问x的时间差,clock - time[x]
public int longestCycle(int[] edges) {
int n = edges.length, ans = -1;
var time = new int[n];
for (int i = 0, clock = 1; i < n; ++i) {
if (time[i] > 0) continue; // 访问过了
int x = i, startTime = clock;
while (x >= 0) {
if (time[x] > 0) { // 重复访问
//判断是找到了一个环,还是访问了一个之前找环过程中访问的点
if (time[x] >= startTime){// 找到了一个新的环
ans = Math.max(ans, clock - time[x]);
// 如果要输出环上所有的点,要怎么做?
System.out.println(x);
int y = edges[x];
while(y != x){
System.out.println(y);
y = edges[y];
}
}
break;
}
time[x] = clock++;
x = edges[x];
}
}
return ans;
}
}
2509. 查询树中环的长度
难度困难18
给你一个整数 n ,表示你有一棵含有 2n - 1 个节点的 完全二叉树 。根节点的编号是 1 ,树中编号在[1, 2n - 1 - 1] 之间,编号为 val 的节点都有两个子节点,满足:
- 左子节点的编号为
2 * val - 右子节点的编号为
2 * val + 1
给你一个长度为 m 的查询数组 queries ,它是一个二维整数数组,其中 queries[i] = [ai, bi] 。对于每个查询,求出以下问题的解:
- 在节点编号为
ai和bi之间添加一条边。 - 求出图中环的长度。
- 删除节点编号为
ai和bi之间新添加的边。
注意:
- 环 是开始和结束于同一节点的一条路径,路径中每条边都只会被访问一次。
- 环的长度是环中边的数目。
- 在树中添加额外的边后,两个点之间可能会有多条边。
请你返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 个查询的结果*。*
示例 1:
输入:n = 3, queries = [[5,3],[4,7],[2,3]]
输出:[4,5,3]
解释:上图是一棵有 23 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 3 和节点 5 之间添加边后,环为 [5,2,1,3] ,所以第一个查询的结果是 4 。删掉添加的边后处理下一个查询。
- 在节点 4 和节点 7 之间添加边后,环为 [4,2,1,3,7] ,所以第二个查询的结果是 5 。删掉添加的边后处理下一个查询。
- 在节点 2 和节点 3 之间添加边后,环为 [2,1,3] ,所以第三个查询的结果是 3 。删掉添加的边。
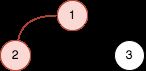
示例 2:
输入:n = 2, queries = [[1,2]]
输出:[2]
解释:上图是一棵有 22 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 1 和节点 2 之间添加边后,环为 [2,1] ,所以第一个查询的结果是 2 。删掉添加的边。
提示:
2 <= n <= 30m == queries.length1 <= m <= 105queries[i].length == 21 <= ai, bi <= 2n - 1ai != bi
class Solution {
/**
完全二叉树 节点编号的性质
深度越深,节点编号越大,严格大于上一层节点的编号
在 a 和 b 之间连边
环长就是dist(LCA, a) + dist(LCA, b) + 1
如何求 a 和 b 的最近公共祖先?
利用完全二叉树的性质:每次选择节点编号更大的数 进行/2操作(找父节点操作)
*/
public int[] cycleLengthQueries(int n, int[][] q) {
int[] ans = new int[q.length];
for(int i = 0; i < q.length; i++){
int res = 1;
int a = q[i][0], b = q[i][1];
while(a != b){ // 如果中间遇不到,最后一定会在a=b=1处相遇
if(a > b) a /= 2;
else b /= 2;
res++; // 每往上走一步,环长+1
}
ans[i] = res;
}
return ans;
}
}
2392. 给定条件下构造矩阵
难度困难33
给你一个 正 整数 k ,同时给你:
- 一个大小为
n的二维整数数组rowConditions,其中rowConditions[i] = [abovei, belowi]和 - 一个大小为
m的二维整数数组colConditions,其中colConditions[i] = [lefti, righti]。
两个数组里的整数都是 1 到 k 之间的数字。
你需要构造一个 k x k 的矩阵,1 到 k 每个数字需要 恰好出现一次 。剩余的数字都是 0 。
矩阵还需要满足以下条件:
- 对于所有
0到n - 1之间的下标i,数字abovei所在的 行 必须在数字belowi所在行的上面。 - 对于所有
0到m - 1之间的下标i,数字lefti所在的 列 必须在数字righti所在列的左边。
返回满足上述要求的 任意 矩阵。如果不存在答案,返回一个空的矩阵。
示例 1:
输入:k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
输出:[[3,0,0],[0,0,1],[0,2,0]]
解释:上图为一个符合所有条件的矩阵。
行要求如下:
- 数字 1 在第 1 行,数字 2 在第 2 行,1 在 2 的上面。
- 数字 3 在第 0 行,数字 2 在第 2 行,3 在 2 的上面。
列要求如下:
- 数字 2 在第 1 列,数字 1 在第 2 列,2 在 1 的左边。
- 数字 3 在第 0 列,数字 2 在第 1 列,3 在 2 的左边。
注意,可能有多种正确的答案。
示例 2:
输入:k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
输出:[]
解释:由前两个条件可以得到 3 在 1 的下面,但第三个条件是 3 在 1 的上面。
没有符合条件的矩阵存在,所以我们返回空矩阵。
提示:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti
class Solution {
public int[][] buildMatrix(int k, int[][] rowConditions, int[][] colConditions) {
// 两次拓扑排序,获得行顺序和列顺序
int[] row = top(k, rowConditions);
int[] col = top(k, colConditions);
// **重要:当拓扑序中个数小于k,说明无法按拓扑序遍历所有节点,存在循环引用(不符合条件)
if(row.length < k || col.length < k) return new int[][]{};
int[][] res = new int[k][k];
// 按照拓扑序填入答案数组
for(int i = 0; i < k; i++){
int num = row[i];
int j = 0;
for(; j < k; j++){
if(num == col[j]) break;
}
res[i][j] = num+1;
}
return res;
}
// 获得1-k数字的拓扑序
public int[] top(int k, int[][] condition){
int[] indegree = new int[k];
List<Integer>[] g = new ArrayList[k];
Arrays.setAll(g, e -> new ArrayList<>());
for(int[] c : condition){
int x = c[0]-1, y = c[1]-1; // 下标从0开始,这样子遍历邻接矩阵不需要处理
g[x].add(y);
indegree[y]++;
}
List<Integer> order = new ArrayList<>();
Deque<Integer> dq = new ArrayDeque<>();
for(int i = 0; i < k; i++){
if(indegree[i] == 0) dq.addLast(i);
}
while(!dq.isEmpty()){
int x = dq.pollFirst();
order.add(x);
for(int y : g[x]){
if(--indegree[y] == 0) dq.addLast(y);
}
}
return order.stream().mapToInt(Integer::intValue).toArray();
}
}
2467. 树上最大得分和路径
难度中等18
一个 n 个节点的无向树,节点编号为 0 到 n - 1 ,树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 在树中有一条边。
在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ,其中 amount[i] 表示:
- 如果
amount[i]的值是负数,那么它表示打开节点i处门扣除的分数。 - 如果
amount[i]的值是正数,那么它表示打开节点i处门加上的分数。
游戏按照如下规则进行:
-
一开始,Alice 在节点
0处,Bob 在节点bob处。 -
每一秒钟,Alice 和 Bob 分别 移动到相邻的节点。Alice 朝着某个 叶子结点 移动,Bob 朝着节点
0移动。 -
对于他们之间路径上的
每一个
节点,Alice 和 Bob 要么打开门并扣分,要么打开门并加分。注意:
- 如果门 已经打开 (被另一个人打开),不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时 到达一个节点,他们会共享这个节点的加分或者扣分。换言之,如果打开这扇门扣
c分,那么 Alice 和 Bob 分别扣c / 2分。如果这扇门的加分为c,那么他们分别加c / 2分。
-
如果 Alice 到达了一个叶子结点,她会停止移动。类似的,如果 Bob 到达了节点
0,他也会停止移动。注意这些事件互相 独立 ,不会影响另一方移动。
请你返回 Alice 朝最优叶子结点移动的 最大 净得分。
示例 1:
输入:edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
输出:6
解释:
上图展示了输入给出的一棵树。游戏进行如下:
- Alice 一开始在节点 0 处,Bob 在节点 3 处。他们分别打开所在节点的门。
Alice 得分为 -2 。
- Alice 和 Bob 都移动到节点 1 。
因为他们同时到达这个节点,他们一起打开门并平分得分。
Alice 的得分变为 -2 + (4 / 2) = 0 。
- Alice 移动到节点 3 。因为 Bob 已经打开了这扇门,Alice 得分不变。
Bob 移动到节点 0 ,并停止移动。
- Alice 移动到节点 4 并打开这个节点的门,她得分变为 0 + 6 = 6 。
现在,Alice 和 Bob 都不能进行任何移动了,所以游戏结束。
Alice 无法得到更高分数。
示例 2:
输入:edges = [[0,1]], bob = 1, amount = [-7280,2350]
输出:-7280
解释:
Alice 按照路径 0->1 移动,同时 Bob 按照路径 1->0 移动。
所以 Alice 只打开节点 0 处的门,她的得分为 -7280 。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树。1 <= bob < namount.length == namount[i]是范围[-104, 104]之间的一个 偶数 。
class Solution {
// Alice 朝着某个 叶子结点 移动,Bob 朝着节点 0 移动。
// bob的移动路径是确定的
// DFS求出bob的路径,计算到达每个点的时间(不在路径上的点,初始化成无穷大/n)
// DFS 从0到每个叶子节点,按照题目要求累加amount,在叶子节点更新答案的最大值
List<Integer>[] g;
int[] bobtime;
int[] amount;
int res = Integer.MIN_VALUE;
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
int n = amount.length;
this.amount = amount;
bobtime = new int[n];
Arrays.fill(bobtime, n);
// 建图
g = new ArrayList[n];
Arrays.setAll(g, e-> new ArrayList<>());
for(int[] e : edges){
int x = e[0], y = e[1];
g[x].add(y);
g[y].add(x);
}
//bob的路线固定 先dfs出 bob 的路线
dfsB(bob, -1, 0); //从bob点出发 走向 0, 初始父节点为 -1
g[0].add(-1); //防止0节点被误认为叶子节点
dfsA(0, -1, 0, 0); //寻找从0节点出发 到达叶子节点的最优路线
return res;
}
public boolean dfsB(int x, int fa, int time){
if(x == 0){ //到达0点 记录时间
bobtime[x] = time;
return true;
}
boolean flag = false;
for(int y : g[x]){
if(y != fa && dfsB(y, x, time+1)){
flag = true;
break;
}
}
//最后判断bob是否到达0点,真的到达了才记录时间
if(flag) bobtime[x] = time;
return flag;
}
public void dfsA(int x, int fa, int time, int total){
if(bobtime[x] > time){ // 比bob早到x节点
total += amount[x];
}else if(bobtime[x] == time){ // 和bob同一时间到
total += amount[x] / 2;
}
// 到达叶子节点
if(g[x].size() == 1) res = res > total ? res : total;
for(int y : g[x]){
if(y != fa) dfsA(y, x, time+1, total);
}
}
}
2493. 将节点分成尽可能多的组
难度困难18收藏分享切换为英文接收动态反馈
给你一个正整数 n ,表示一个 无向 图中的节点数目,节点编号从 1 到 n 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 双向 边。注意给定的图可能是不连通的。
请你将图划分为 m 个组(编号从 1 开始),满足以下要求:
- 图中每个节点都只属于一个组。
- 图中每条边连接的两个点
[ai, bi],如果ai属于编号为x的组,bi属于编号为y的组,那么|y - x| = 1。
请你返回最多可以将节点分为多少个组(也就是最大的 m )。如果没办法在给定条件下分组,请你返回 -1 。
示例 1:
输入:n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
输出:4
解释:如上图所示,
- 节点 5 在第一个组。
- 节点 1 在第二个组。
- 节点 2 和节点 4 在第三个组。
- 节点 3 和节点 6 在第四个组。
所有边都满足题目要求。
如果我们创建第五个组,将第三个组或者第四个组中任何一个节点放到第五个组,至少有一条边连接的两个节点所属的组编号不符合题目要求。
示例 2:
输入:n = 3, edges = [[1,2],[2,3],[3,1]]
输出:-1
解释:如果我们将节点 1 放入第一个组,节点 2 放入第二个组,节点 3 放入第三个组,前两条边满足题目要求,但第三条边不满足题目要求。
没有任何符合题目要求的分组方式。
提示:
1 <= n <= 5001 <= edges.length <= 104edges[i].length == 21 <= ai, bi <= nai != bi- 两个点之间至多只有一条边。
class Solution {
/**
从树开始推测性质:
1. 树是一定可以的
2. 答案和选择开始编号的起点有关
图 with 环
猜想: 环长为奇数 => -1
|y - x| = 1
从 x 到 y(走一步),编号的奇偶性一定变了
奇环: return -1
==> 必要条件:图中只有偶环
充分条件:偶环 =>一定可以构造出答案
1. 判断所有连通块是否为二分图红蓝染色法(一开始所有点都是白色的)如果不是,返回 -1
2. 对连通块内的所有点,暴力枚举,当成是 BFS 的起点,然后跑一遍得到最大编号
3. 连通块的初始编号,等于上一个连通块的最大编号+1
*/
private List<Integer>[] g;
private List<Integer> nodes;
private int[] time, color; // time 充当 vis 数组的作用(避免在 BFS 内部重复创建 vis 数组)
private int clock = 0; // clock变量在每次bfs前自增,然后复用time数组
public int magnificentSets(int n, int[][] edges) {
g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for(int[] e : edges){
int x = e[0]-1, y = e[1]-1;
g[x].add(y);
g[y].add(x);
}
color = new int[n]; // 判断是否二分图,同时充当vis数组
time = new int[n];
nodes = new ArrayList<>(); // 将连通块的节点都拿出来
int ans = 0;
for(int i = 0; i < n; i++){
if(color[i] != 0) continue; // 已经访问过这个连通块了
nodes.clear();
if(!isBipartite(i, 1)) return -1; // 如果不是二分图(有奇环),则无法分组
// 否则一定可以分组
int maxDepth = 0;
for(int x : nodes){ // 枚举连通块的每个点,作为起点 BFS,求最大深度
maxDepth = Math.max(maxDepth, bfs(x));
}
ans += maxDepth;
}
return ans;
}
public boolean isBipartite(int x, int c){
color[x] = c;
nodes.add(x);
for(int y : g[x]){
// 用-c表示一种颜色,尝试将x的邻接节点都染上另一种颜色
if(color[y] == c || color[y] == 0 && !isBipartite(y, -c))
return false;
}
return true;
}
// 在连通块中进行bfs,返回最大编号(深度)
public int bfs(int start){
int depth = 0;
time[start] = ++clock;
List<Integer> q = new ArrayList<>();
q.add(start);
while(!q.isEmpty()){
List<Integer> tmp = q;
q = new ArrayList<>();
for(int x : tmp){
for(int y : g[x]){
if(time[y] != clock){ // 没有在同一次BFS
time[y] = clock;
q.add(y);
}
}
}
depth++;
}
return depth;
}
}