2023.2.12 第四十次周报
目录
前言
文献阅读-用于预测时间序列的网络自关注
背景
贡献
主要思路
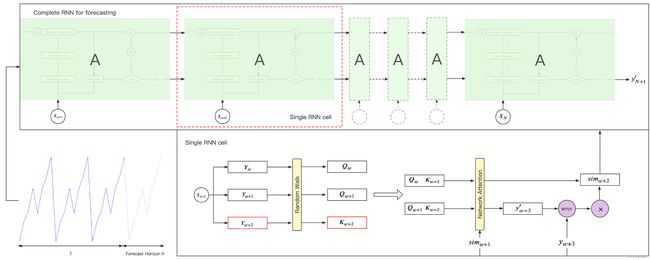
预测模型
可见性图
随机游走过程
进行预测
总结与展望
元胞自动机 Cellular Automata
概述
元胞自动机的构成
元胞自动机的基本特征
分类
总结
前言
This week I learned an article that proposed network self-attention to measure similarity between nodes in a network. A novel RNN based on network self-attention is proposed for time series forecasting.In network attention, the feature matrix of nodes is obtained through a random walk process. Then, the similarity score between the nodes is calculated and normalized to the similarity distribution by Softmax. Finally, the network attention value is calculated by weighted summation.In addition, in terms of machine learning, the relevant content of cellular automata was learned.
本周学习了一篇文章,该文提出网络自注意力来衡量网络中节点之间的相似性。并提出了一种基于网络自注意力的新型RNN用于时间序列预测。在网络注意力中,通过随机游走过程获得节点的特征矩阵。然后,计算节点之间的相似性得分,并通过Softmax将其归一化为相似性分布。最后,通过加权求和计算网络注意力值。除此之外,在机器学习方面,学习了元胞自动机的相关内容。
文献阅读-用于预测时间序列的网络自关注
--Yuntong Hu, Fuyuan Xiao,
Network self attention for forecasting time series,
Applied Soft Computing,
Volume 124,
2022,
109092,
ISSN 1568-4946,
https://doi.org/10.1016/j.asoc.2022.109092.
背景
时间序列预测旨在通过分析时间序列的历史值来预测时间序列,在预测能源消耗,股价,流行病等各个领域起着重要作用。因此,高精度的预测模型具有重要的实践价值。自从基于自我注意的Transformer在NLP中取得巨大成功以来,注意力机制最近被应用于各个领域来解决不同的问题。注意力机制的本质是从输入到输出分配全局依赖关系。它是一个独立于任何模型的通用框架。由于其有可能找到输入向量和输出之间的内部关系,它也已被应用于预测时间序列。通过注意力机制,可以深入探讨时间序列中节点之间的相关性。因此,利用可见性图和注意力机制的优势,提出了一种新的基于网络的时间序列预测模型。时间序列通过可见性算法转换为网络。然后,通过基于网络自注意的递归神经网络(RNN)计算节点之间的相似度得分,其中通过随机游走获得节点的初始特征矩阵。
贡献
1.该文提出一种基于注意力机制的时间序列预测方法。
2.网络中节点的相似性分布由网络自注意来衡量。
3.相似性分布由局部特征和全局特征生成。
4.实验结果验证了所提方法的有效性。
主要思路
本文首先提出了网络自我关注。在网络自注意中,节点的特征矩阵是通过在窗口大小的子VG内随机游走获得的。然后,通过基于余弦相似度和 Sigmoid 函数的相似性函数计算节点之间的相似性得分,然后由 Softmax 将相似性得分归一化为相似性分布。最后,得到网络注意力值。此外,我们设计了一种循环神经网络(RNN)来学习网络的相似性得分,并基于该网络提出了一种新的时间序列预测模型。为了测试我们方法的预测准确性,我们预测了CCI,M1和M3数据集。 5种误差测量包括MAE,MAPE,sMAPE,RMSE和NRMSE用于计算误差。我们在预测 M1 和 M3 数据集时讨论了该方法的参数。
预测模型
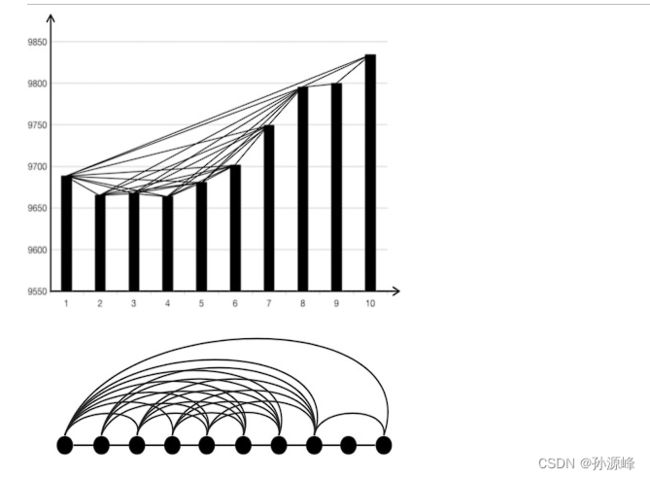
可见性图
随机游走过程
进行预测
总结与展望
该文提出网络自注意力来衡量网络中节点之间的相似性。并提出了一种基于网络自注意力的新型RNN用于时间序列预测。在网络注意力中,通过随机游走过程获得节点的特征矩阵。然后,计算节点之间的相似性得分,并通过Softmax将其归一化为相似性分布。最后,通过加权求和计算网络注意力值。
为了预测时间序列,我们设计了一种基于网络自我注意的新型递归神经网络(RNN)来学习相似性得分。然后,通过Softmax对时间序列的学习相似性得分进行归一化。然后,得到时间序列的最终网络注意力值,并据此对时间序列进行预测。
实验结果表明,所提预测方法具有良好的性能,也表明网络自注意力对网络中节点相似性的度量能力较强。在预测M1和M3数据集时,所提出的方法在预测M1_yearly、M1_monthly和M3_yearly方面表现最佳(见表3)。在预测其他数据集时,我们的方法与最佳执行方法之间的差异也非常接近。同时,我们的方法也具有良好的鲁棒性(见表5)。
尽管所提出的预测模型表现良好,但仍有几个问题需要解决以提高准确性。我们未来的工作将集中在以下几点:
(1)用更有效的方法代替随机游走过程来生成节点的特征矩阵;
(2)开发一种在学习相似度得分的同时选择标准节点的方法,以提高大数据预测时间序列的训练过程效率;
(3)将网络自我注意的应用扩展到网络的信息量和相似性度量。
元胞自动机 Cellular Automata
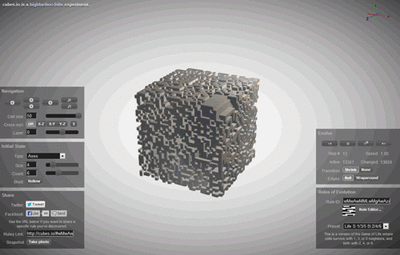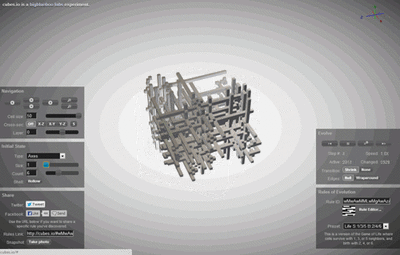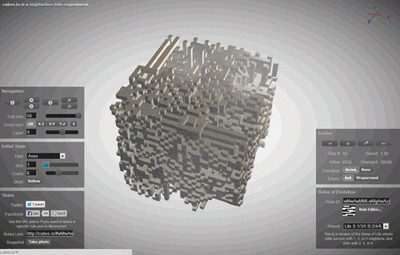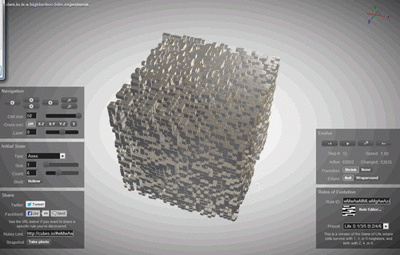
元胞自动机 cellular automata(CA) ,中文也译作细胞自动机、点格自动机、分子自动机或单元自动机,是一种时间、空间、状态都离散,空间相互作用和时间因果关系为局部的网格动力学模型,具有模拟复杂系统时空演化过程的能力。元胞自动机广泛应用于计算机科学、物理学、复杂系统 Complex Systems,理论生物学和微观结构模型等领域。元胞自动机同时也被称为元胞空间,棋盘自动机 tessellation automata,同质结构,元胞结构,棋盘结构和迭代数组。
概述
元胞自动机(Cellular Automata,简称CA)。
把一个空间划分成网络,每一个点表示一个元胞,它们的状态赋值,在网格中用颜色的变化来表示,在事先设定的规则下,元胞的演化就用网格颜色的变化来描述,这样的模型就是元胞自动机。
通过对元胞自动机这些网络中的格点的不同定义,以及初始条件的不同,可以模拟出不同的现象和过程。
它体现了整体辩证思想:用简单的局域相互作用表现复杂系统的整体行为及其时间演化。元胞自动机有三个显著的特点,即大规模同步并行、局域相互作用和结构简单。这些特点使其能高效地模拟许多复杂现象。
元胞自动机的构成
标准元胞自动机是一个由「元胞、元胞状态、邻域和状态更新规则」构成的四元组,用数学符号可以表示为A=(L,d,S,N,f)
- A代表一个元胞自动机系统
- L表示元胞空间
- d表示元胞自动机内元胞空间的维数,是一正整数
- S是元胞有限的、离散的状态集合
- N表示某个邻域内所有元胞的集合
- f表示局部映射或局部规则。
元胞自动机的基本特征
离散性:元胞自动机是高度离散的。它不仅仅空间离散时间离散,而且在函数值,即元胞的状态值也是离散的。
动力学演化的同步性:元胞自动机具有利用简单的,局部规则的和离散的方法,描述复杂的,全部的和连续系统的能力。
相互作用的局部性:元胞自动机的规则是局部的,而动力学行为规则是全局的,在模拟的过程中,具体的演化过程也是局部的,即仅同周围的元胞有关系。
分类
(1)平稳型:自任何初始状态开始,经过一定时间运行后,元胞空间趋于一个空间平稳的构形,这里空间平稳即指每一个元胞处于固定状态。不随时间变化而变化。
(2)周期型:经过一定时间运行后,元胞空间趋于一系列简单的固定结构 Stable Paterns 或周期结构 Perlodical Patterns。由于这些结构可看作是一种滤波器 Filter,故可应用到图像处理的研究中。
(3)混沌型:自任何初始状态开始,经过一定时间运行后,元胞自动机表现出混沌的非周期行为,所生成的结构的统计特征不再变化,通常表现为分形分维特征。
(4)复杂型:出现复杂的局部结构,或者说是局部的混沌,其中有些会不断地传播。从另一角度,元胞自动机可视为动力系统,因而可将初试点、轨道、不动点、周期轨和终极轨等一系列概念用到元胞自动机的研究中。
从另一角度,元胞自动机可视为动力系统,因而可将初始点、轨道、不动点、周期轨和终极轨等一系列概念用到元胞自动机的研究中,上述分类,又可以分别描述为:
(1)均匀状态,即点态吸引子,或称不动点;
(2)简单的周期结构,即周期性吸引子,或称周期轨;
(3)混沌的非周期性模式,即混沌吸引子;
(4)这第四类行为可以与生命系统等复杂系统中的自组织现象相比拟,但在连续系统中没有相对应的模式。
但从研究元胞自动机的角度讲,最具研究价值的具有第四类行为的元胞自动机,因为这类元胞自动机被认为具有突现计算 Emergent Computation功能,研究表明,可以用作广义计算机 Universal Computer 以仿真任意复杂的计算过程。另外,此类元胞自动机在发展过程中还表现出很强的不可逆 Irreversibility 特征,而且,这种元胞自动机在若干有限循环后,有可能会 "死"掉,即所有元胞的状态变为零。
总结
下周我们将继续学习机器学习的相关内容。除此之外,将深层次的研究时序问题。