如何战胜AI?唯努力尔-- DSP算法的FPGA实现指南
如何战胜AI?唯努力尔! DSP算法的FPGA实现指南!
来一集番外。
 而这 也是开坑的第一个算法!我们先讲案例再谈实现指南
而这 也是开坑的第一个算法!我们先讲案例再谈实现指南
文章目录
- 如何战胜AI?唯努力尔! DSP算法的FPGA实现指南!
-
- 观前提醒
- 实用算法原理
- 数学原理
- 代码模块划分与实现
-
- FIR滤波器
- 误差计算与系数更新模块
- 最终代码
- DSP算法的FPGA实现指南
- 小结
观前提醒
本期主题 : 基于Verilog的LMS自适应滤波算法实现
选择这个主题的原因也是LMS本身也是采用类似梯度下降的方法所实现的自适应算法。本文的代码含金量较高,建议先阅读文字后细品代码,收获更加丰富
内容不感兴趣也可以直奔小结,会有小何最近的一些收获体会
注意:未看到小结之前,本文一个字都不值得信任
首先,我们可以先由一个大概的概念来初定这次的设计:
- 确定需要滤波的信号类型和滤波器的类型:例如,可能需要设计一个LMS或RLS自适应滤波器。
- 确定需要的输入输出接口。考虑到自适应滤波器是在实时信号处理应用中使用的,需要考虑到输入信号的采样率和数据宽度,以及输出信号的数据宽度。
- 基于选择的滤波器类型,编写Verilog代码来描述滤波器结构和算法。根据自适应滤波器的算法,需要定义各种变量和参数。例如,可能需要定义滤波器的权重向量,误差信号,步长等。
- 编写TestBench以验证Verilog代码的功能。
- 进行仿真并分析结果。
- 进行硬件测试并优化设计以满足性能和功耗要求。
实用算法原理
LMS(最小均方)算法是一种自适应滤波算法,用于调整滤波器系数以适应输入信号的统计特性。LMS算法基于误差信号的平方和最小化来更新滤波器系数。以下是LMS自适应滤波器的主要公式和步骤:
- 滤波器输出 LMS自适应滤波器的滤波器输出 y [ n ] y[n] y[n]可以通过将滤波器系数 w [ n ] \boldsymbol{w}[n] w[n]和输入信号 x [ n ] \boldsymbol{x}[n] x[n]的卷积计算得到:
y [ n ] = ω T [ n ] x [ n ] y[n] =\boldsymbol{\omega}^T[n] \boldsymbol{x}[n] y[n]=ωT[n]x[n]
其中, w T [ n ] \boldsymbol{w}^T[n] wT[n]表示滤波器系数的转置。
- 期望输出
期望输出 d [ n ] d[n] d[n]是滤波器应该输出的理想信号。在LMS自适应滤波器中,期望输出通常是输入信号经过某些变换之后的结果。例如,在语音信号处理中,期望输出可以是预测误差,即预测的信号和实际信号之间的差异。
- 误差信号
误差信号 e [ n ] e[n] e[n]表示实际输出和期望输出之间的差异:
e [ n ] = d [ n ] − y [ n ] e[n]=d[n]−y[n] e[n]=d[n]−y[n]
- 系数更新
系数向量 w [ n ] \boldsymbol{w}[n] w[n]的更新可以通过以下公式计算:
w [ n + 1 ] = w [ n ] + μ e [ n ] x [ n ] w[n+1]=w[n]+\mu e[n]x[n] w[n+1]=w[n]+μe[n]x[n]
其中, μ \mu μ是步长参数,控制每次更新的系数向量的大小。 x [ n ] \boldsymbol{x}[n] x[n]是输入信号的向量表示。
LMS自适应滤波器的主要思想是,通过使用误差信号来调整滤波器的系数,从而使滤波器的输出逐渐接近期望输出。这个过程可以迭代进行,直到误差信号达到一个足够小的值或者系数向量达到一个稳定状态为止。
数学原理
以上原理比较实用主义,下面我们从数学的角度证明这个系数更新方式为什么会起到作用。
当使用LMS自适应滤波器时,我们的目标是通过更新滤波器系数 w [ n ] \boldsymbol{w}[n] w[n] 来最小化误差信号 e [ n ] e[n] e[n]。LMS算法使用梯度下降的思想来实现这个目标,即通过每次更新系数向量 w [ n ] \boldsymbol{w}[n] w[n] 来沿着误差信号的负梯度方向逐步调整滤波器的输出。
我们可以从最小化误差信号的角度来推导LMS算法中系数更新的公式。误差信号 e [ n ] e[n] e[n] 定义为:
e [ n ] = d [ n ] − y [ n ] = d [ n ] − ω T [ n ] x [ n ] e[n]=d[n]−y[n]=d[n]−\omega^T[n]x[n] e[n]=d[n]−y[n]=d[n]−ωT[n]x[n]
其中, d [ n ] d[n] d[n] 为期望输出, y [ n ] y[n] y[n] 为滤波器的实际输出。我们的目标是最小化误差信号的平方和 J ( n ) = 1 2 e 2 [ n ] J(n) = \frac{1}{2}e^2[n] J(n)=21e2[n]。因此,我们需要找到 w [ n ] \boldsymbol{w}[n] w[n] 的最优值 w ∗ \boldsymbol{w}^* w∗,使得 J ( n ) J(n) J(n) 最小:
w ∗ = arg min ω [ n ] J ( n ) w ^∗ =\arg\min_{\omega[n]} J(n) w∗=argω[n]minJ(n)
我们可以使用梯度下降算法来求解这个最小化问题。具体来说,我们需要计算 J ( n ) J(n) J(n) 对 w [ n ] \boldsymbol{w}[n] w[n] 的梯度:
∇ w [ n ] J ( n ) = ∂ J ( n ) ∂ ω [ n ] \nabla w[n] J(n)= \frac{\partial J(n)}{\partial \omega[n]} ∇w[n]J(n)=∂ω[n]∂J(n)
根据链式法则,可以得到:
∂ J ( n ) ∂ ω [ n ] = ∂ J ( n ) ∂ e [ n ] ∂ e [ n ] ∂ ω [ n ] \frac{\partial J(n)}{\partial \omega[n]} = \frac{\partial J(n)}{\partial e[n]}\frac{\partial e[n]}{\partial \omega[n]} ∂ω[n]∂J(n)=∂e[n]∂J(n)∂ω[n]∂e[n]
将 e [ n ] e[n] e[n] 的定义代入上式得到:
∂ J ( n ) ∂ ω [ n ] = − e [ n ] x [ n ] \frac{\partial J(n)}{\partial \omega[n]} = -e[n]x[n] ∂ω[n]∂J(n)=−e[n]x[n]
因此,我们可以使用以下公式来更新系数向量 w [ n ] \boldsymbol{w}[n] w[n]:
w [ n + 1 ] = w [ n ] + μ e [ n ] x [ n ] w[n+1]=w[n]+\mu e[n]x[n] w[n+1]=w[n]+μe[n]x[n]
其中, μ \mu μ 是步长参数,用于控制每次更新的大小。这个更新公式就是LMS算法中系数更新的公式。
可以证明,如果满足一些条件,LMS算法可以实现误差信号的最小化。具体来说,如果输入信号的自相关矩阵是正定的且滤波器的步长参数 μ \mu μ 满足一些约束条件,LMS算法可以收敛到最优解。因此,LMS算法被广泛应用于自适应滤波、信号处理、通信等领域。
代码模块划分与实现
对于实现一个LMS自适应滤波器,可以将其划分为以下几个模块:
- 输入接口模块:该模块接受输入信号,可能是从ADC转换器接收信号,并将其传递到下一个模块。
- FIR滤波器模块:该模块包括一个FIR滤波器,其系数需要更新以适应输入信号的变化。滤波器的输出被传递到误差计算模块。
- 误差计算模块:该模块将FIR滤波器的输出与期望的输出进行比较,并计算误差信号。误差信号将传递到系数更新模块。
- 系数更新模块:该模块根据误差信号和其他参数,例如步长和滤波器的系数向量,更新滤波器的系数。更新后的系数将返回到FIR滤波器模块,以更新滤波器的系数。
- 输出接口模块:该模块将自适应滤波器的输出发送到DAC转换器,以便将其转换为模拟信号输出。
这里我们就跳过输入接口模块了,这个模块中主要是大家使用的ADC不一样,具体要求的物理速率和要求不一样。
FIR滤波器
我们先来实现一个简单的FIR滤波器,然后再拓展到专用于LMS自适应滤波的FIR滤波器实现中
使用LMS自适应滤波器时,我们需要使用一个FIR滤波器来对输入信号进行滤波。在Verilog中,我们可以使用以下代码来实现一个简单的FIR滤波器模块:
module fir_filter (
input clk,
input rst_n,
input signed [15:0] data_in,
output reg signed [15:0] data_out
);
// Coefficients of FIR filter
parameter signed [15:0] coeffs[0:9] = {3277, 6553, 9830, 13107, 16384, -13107, -9830, -6553, -3277, 0};
// Internal registers for delay line and coefficient storage
reg signed [15:0] delay_line[0:9];
reg signed [15:0] coeffs_reg[0:9];
// Update delay line and coefficient registers
always @(posedge clk or negedge rst_n) begin
if (~rst_n) begin
delay_line <= '0;
coeffs_reg <= '0;
end else begin
delay_line[0] <= data_in;
coeffs_reg[0] <= coeffs[0];
for (i = 1; i <= 9; i = i + 1) begin
delay_line[i] <= delay_line[i-1];
coeffs_reg[i] <= coeffs[i];
end
end
end
// Compute filtered output
always @(posedge clk or negedge rst_n) begin
if (~rst_n) begin
data_out <= '0;
end else begin
data_out <= (delay_line * coeffs_reg);
end
end
endmodule
以上是一个固定系数的FIR滤波器,但在LMS滤波器中,系数是随时间变化的,所以我们只稍加修改就可以变成我们所需要的FIR滤波器了,但这会在文末再进行集成.
误差计算与系数更新模块
比较简单
module lms_error_calculation(
input signed [15:0] x,
input signed [15:0] y,
input signed [15:0] coeff,
output signed [31:0] error
);
wire signed [31:0] mult_result;
assign mult_result = x * coeff;
assign error = y - mult_result;
endmodule
module lms_coeff_update(
input signed [31:0] error,
input signed [15:0] x,
input signed [15:0] coeff,
input signed [15:0] step_size,
output signed [15:0] new_coeff
);
wire signed [31:0] mult_result;
wire signed [31:0] step_size_mult;
wire signed [31:0] error_mult;
wire signed [31:0] coeff_diff;
assign mult_result = x * error;
assign step_size_mult = step_size * mult_result;
assign error_mult = error * error;
assign coeff_diff = step_size_mult / (error_mult + 1);
assign new_coeff = coeff + coeff_diff;
endmodule
最终代码
根据以上模块,糅合一下就可以得到最终代码:
module fir_lms
(
input clk,
input rst,
input signed [15:0] x,
input signed [15:0] d,
input signed [15:0] alpha,
output signed [15:0] y,
output reg [15:0] [0:FIR_LEN-1] coeffs
);
parameter FIR_LEN = 32;
parameter COEFF_BITS = 16;
reg signed [15:0] [0:FIR_LEN-1] taps;
reg signed [15:0] [0:FIR_LEN-1] x_delay;
reg signed [15:0] error;
reg signed [15:0] temp;
wire signed [31:0] mul;
wire signed [31:0] acc;
reg signed [15:0] y_int;
reg signed [15:0] y_frac;
integer i;
always @(posedge clk) begin
if (rst) begin
for (i = 0; i < FIR_LEN; i = i + 1) begin
coeffs[i] <= 0;
taps[i] <= 0;
x_delay[i] <= 0;
end
end
else begin
// Shift input data into delay line
x_delay[0] <= x;
for (i = 1; i < FIR_LEN; i = i + 1) begin
x_delay[i] <= x_delay[i-1];
end
// FIR filter
acc <= 0;
for (i = 0; i < FIR_LEN; i = i + 1) begin
mul <= taps[i] * x_delay[i];
acc <= acc + mul;
end
y_int <= acc >> COEFF_BITS;
y_frac <= acc - (y_int << COEFF_BITS);
y <= y_int;
// Calculate error
error <= d - y;
// Update filter coefficients
for (i = 0; i < FIR_LEN; i = i + 1) begin
temp <= alpha * error * x_delay[i];
coeffs[i] <= coeffs[i] + temp;
taps[i] <= coeffs[i];
end
end
end
endmodule
DSP算法的FPGA实现指南
- 确定算法类型:首先,你需要明确要实现的DSP算法类型,例如滤波器、FFT、FIR、IIR等。
- 确定输入/输出数据格式:确定输入/输出数据格式,包括数据类型(如整数、浮点数、定点数)、位宽和量化精度等。
- 设计算法架构:根据算法类型和数据格式,设计算法的硬件架构。可以采用VHDL或Verilog等硬件描述语言进行设计。
- 选择FPGA器件:根据算法的计算复杂度和延迟要求,选择合适的FPGA器件。
- 实现硬件设计:使用FPGA开发工具,将算法架构转化为硬件电路,并将其实现在目标FPGA器件上。
- 进行仿真验证:使用FPGA开发工具提供的仿真功能,对实现的硬件电路进行验证,确保其正确性。
- 进行性能优化:如果实现的硬件电路性能不满足要求,可以对算法和架构进行优化,以提高其性能和效率。
- 进行集成测试:将硬件电路集成到整个系统中,进行集成测试,确保系统能够正常工作。
- 进行部署和调试:将系统部署到目标平台上,并进行调试和优化,以确保其稳定性和性能。
总的来说,DSP算法的FPGA实现需要从算法类型、数据格式、算法架构等多个方面进行考虑和设计,同时需要进行仿真验证、性能优化、集成测试和部署调试等步骤,才能最终实现一个高效、稳定的DSP算法FPGA系统。
小结
仔细看到这里的观众不好意思啊。
本文 文字,算法与代码均由AI(chatGPT)生成,由小何少部分修改得到。
小何使用chatGPT也有一定时间了,来讲一下最近的心得体会:
- chatGPT确实是一个很好的overview,但不能是很好的tutorial和manual
- 不能寄望他有什么实际的产出,尤其是比较冷门的领域
实际上,上文中的代码大家可以回看一下,基础模块看起来起码还是个人样,但是一涉及到复杂一点的实现他就开始抽风了,甚至并不会考虑时序和实现。而这已经是小何“教育”出来最好的代码了,以下是一些代码鉴赏:
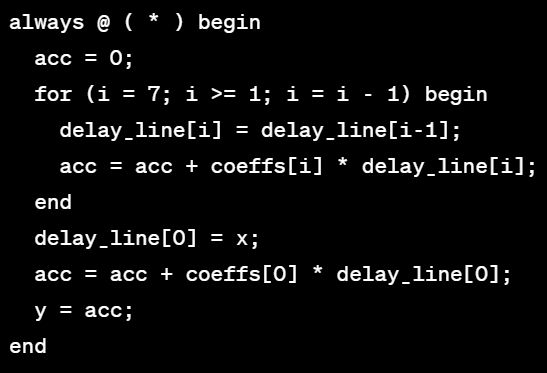
还有:
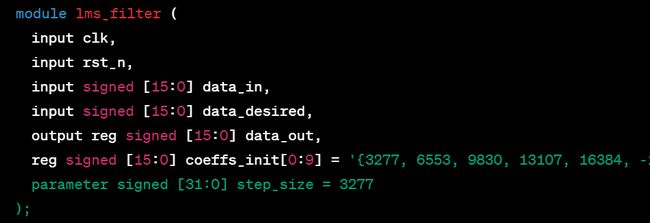
从文中可以看到,算法的描述是非常工程师友好的,对我们工作上需要了解的算法中存在不懂的,问一下chatGPT也是不错的选择。但实际上上文的算法原理和数学原理也是很糟糕的,因为其本质是从结果反推的,能给大家从工程应用的角度告诉他是好使的。而实际上由于他并不是从维纳滤波开始推导起的,所以上文中有一句“如果输入信号的自相关矩阵是正定的且滤波器的步长参数 μ \mu μ 满足一些约束条件,LMS算法可以收敛到最优解” 是无法被解释的。这也是为什么每次小何做DSP算法在FPGA上实现时,总是先一篇原理,一篇实现的原因。
但小何对AI的进一步发展并不持悲观态度,慢慢地小何也认为,好如流浪地球2上550w可以自动对机器进行编程这一点好像也已经慢慢地能实现了。毕竟再强的人类工程师也不可能记住这堕入繁星的技术标准与芯片手册,而AI可以。