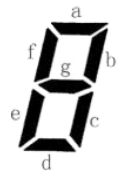图的简单处理（C/C++）

目录

1  存图方法

1.1  邻接矩阵

1.2  邻接表

1.3  链式前向星

2  树形DP

2.1  简介

2.2  例题1：公司聚会

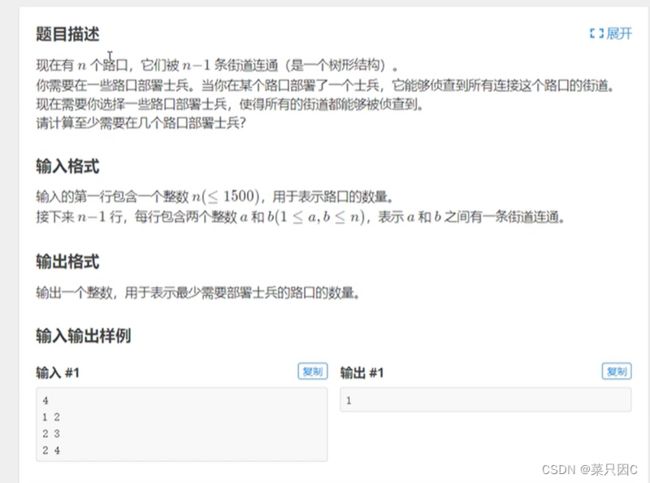
2.3  例题2：士兵部署

2.4  例题3：强力党逗志芃

2.5  例题4：作物杂交（不确定树的结构）

3  并查集

3.1  简介

3.2  模板

3.3  例题

题目描述

4  最小生成树

---

1  存图方法

1.1  邻接矩阵

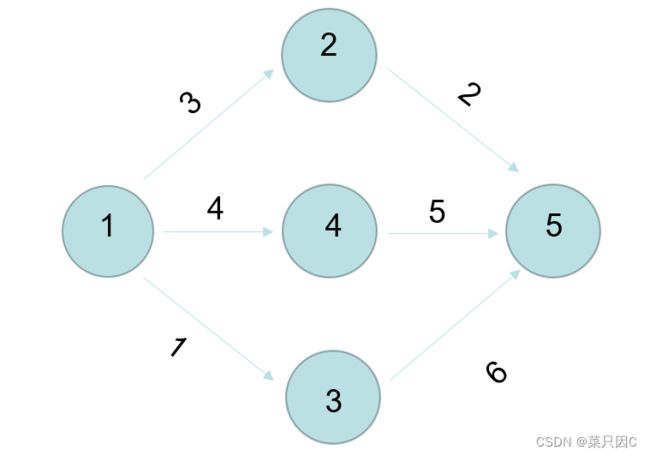
假设有这样一张图：

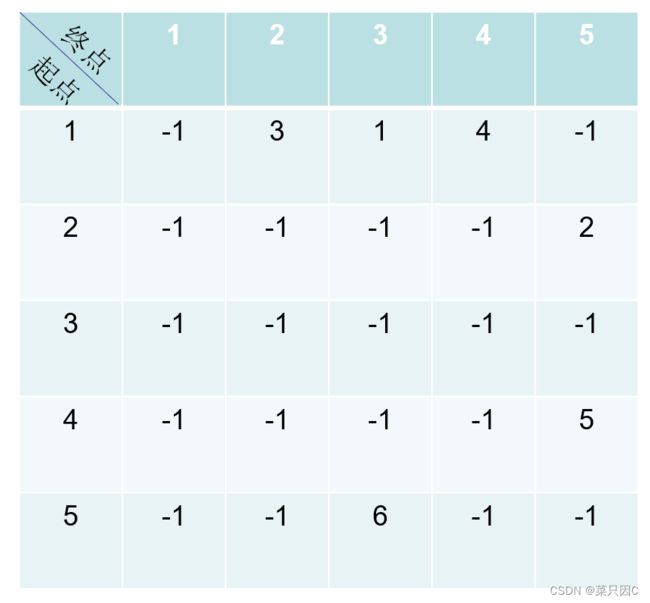
拿一张表存储信息：

 这样可以精确存储每一条路的信息，但发现空间复杂度太大，于是想其他办法优化

1.2  邻接表

假设有这样一张图：

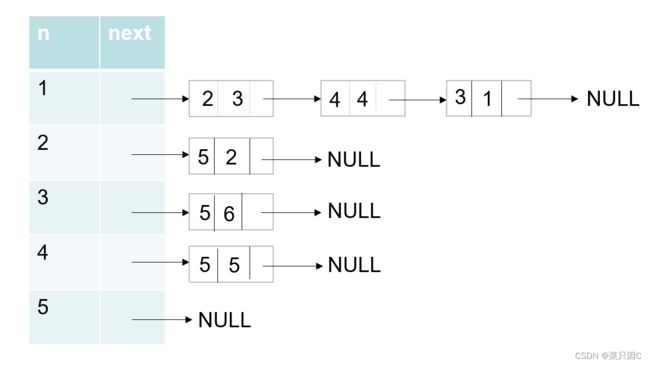
拿这样的图存储信息： 

 其中矩形的第一个框内的信息代表到达的某点的序号，第二个框内的信息代表到达某点消耗的时间，第三个框内的信息代表下一个框的位置

1.3  链式前向星

其实链式前向星就是邻接表

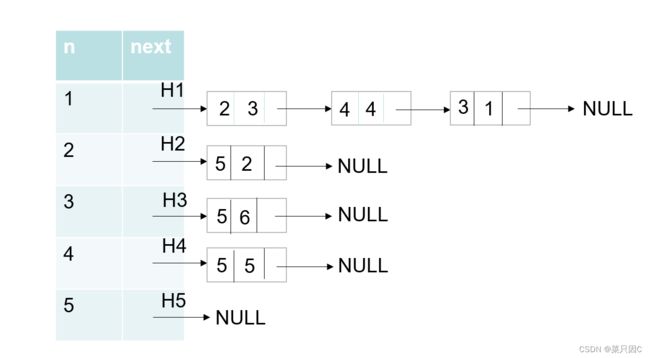
我们做如下变换：

命令头部位置H1,H2,H3,H4,H5得：

 这就是头指针的位置

初始化定义结构体得：

struct E//定义结构体 
{
	int to,w,next;
}Edge[maxm];
int tot,Head[maxm];

遍历有：

for(int i=Head[u];~i;i=Edge[i].next)//遍历 
{
	int v=Edge[i].to;
	int w=Edge[i].w;
	//...
}

如果此时想插入一个点，注意插入一定要从头插，即让新插入的这个点成为第一个点：

void AddEdge(int u,int v,int w)//加点 
{
	Edge[tot].to=v;
	Edge[tot].w=w;
	Edge[tot].next=Head[u];
	Head[u]=tot++;
}

2  树形DP

2.1  简介

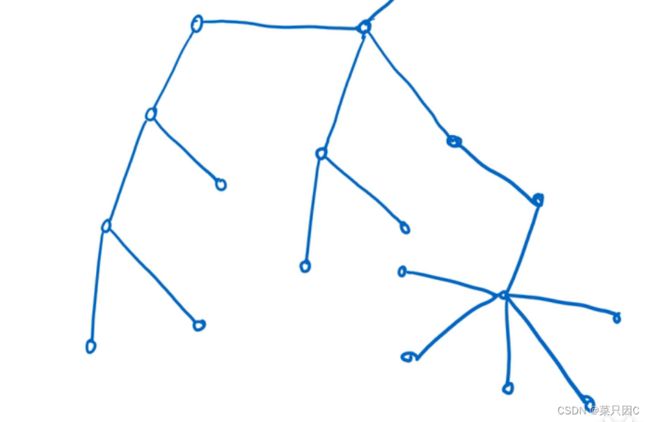
假设有这样一棵树：

 这是一棵无根树

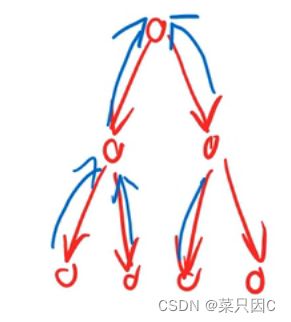
我们随机找一个点作为根结点，可以变成有根树：

我们通过例题讲解具体思路。 

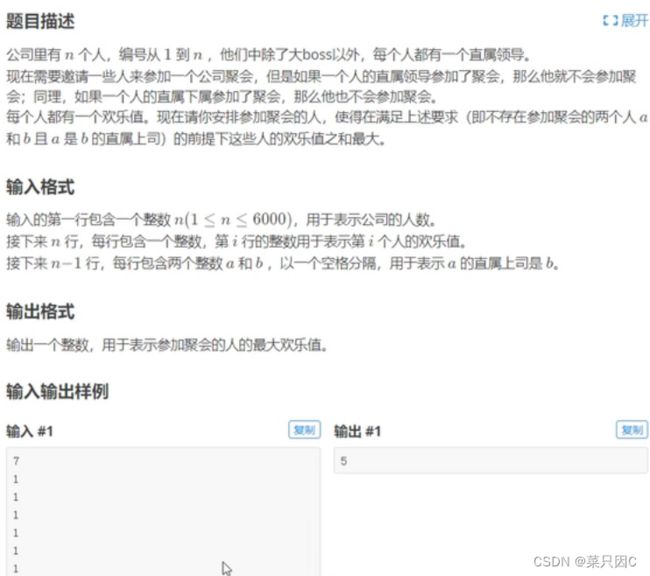
2.2  例题1：公司聚会

 假设u为根结点，定义二维数组dp[][]表示状态

dp[u][0]表示u不参加聚会的情况下以u为根的子树的欢乐值的最大值

dp[u][1]表示u参加聚会的情况下以u为根的子树的欢乐值的最大值 

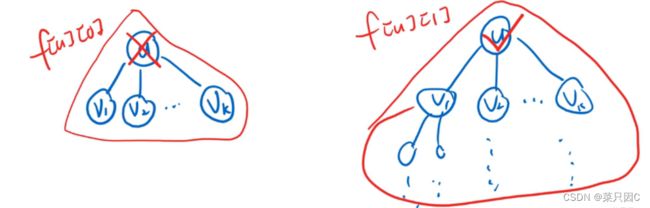
由题意得u参加聚会的情况下子结点v一定不会参加聚会（有一种情况）

u不参加聚会的情况下子结点v不一定参加聚会（有两种情况）

具体解释如图所示：

 那么，我们可以写出不同情况下的状态转移方程：

当u参加聚会时：

当u不参加聚会时：

 其中h【u】代表每个人参加聚会的欢乐值

那么，综合两种情况有：

思路分析完毕，看一下代码：

#include 
using namespace std;
const int maxn=6060;
vector g[maxn];//存储链式前向星用到动态数组
int n,h[maxn],dp[maxn][2],fa[maxn],rt;//rt为根结点
int a,b;
int dfs(int u)
{
	dp[u][1]=h[u];//初始化
	dp[u][0]=0;
	for(int i=0;i

2.3  例题2：士兵部署

 这道题和上道题区别是：

上一道题的父节点如果不参加，子结点的状态不确定

这道题的父节点如果参加，子结点的状态不确定

这道题的状态转移方程有：

 代码（任意选取根结点，这里选取1为根结点）：

#include 
using namespace std;
const int maxn=1510;
int n,dp[maxn][2];
vector g[maxn];

void dfs(int u,int p)//u:当前结点  p:u的父结点 
{
	dp[u][1]=1;
	for(int i=0;i

2.4  例题3：强力党逗志芃

 代码：

#include 
using namespace std;

const int maxn=205;
int n,m;
vectorg[maxn];
int dp[maxn][maxn];
int arr[maxn];
int fa[maxn];
int root;

void dfs(int u)
{
	int sz=g[u].size();
	for(int k=0;k=0;i--)
		{
			for(int j=0;j<=i;j++)
			{
				dp[u][i]=max(dp[u][i],dp[u][i-j]+dp[v][j]);
			}
		}
	}
	for(int i=m;i>=1;i--)  dp[u][i]=dp[u][i-1]+arr[u];
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i>arr[i];
	for(int i=0;i>x>>y;
		x--; y--;
		g[x].push_back(y);
		fa[y]=x;
	}
	for(int i=0;i

2.5  例题4：作物杂交（不确定树的结构）

 代码：

#include
using namespace std;
int    N, M, K, T;
int arr[2005];//种植时间
int les[2005];//对应位置的作物最短的获得时间
const int INF = 0x3f3f3f3f;
map > >m;//int与vector>一一对应的map数据类型
void DFS(int x) 
{//深度优先
    if (les[x] != -1)  return;//判断是否已经对该作物进行过搜索
    les[x] = 0;
    int minv = INF;
    for (int i = 0; i < m[x].size(); i++)
    {
        int l, r;
        l = m[x][i].first;//获取可以得到x作物的其中一种作物
        r = m[x][i].second;//获取可以得到x作物的另一种作物
        DFS(l), DFS(r);//分别对两个作物进行深度优先搜索
        minv = min(minv, max(les[l], les[r]) + max(arr[l], arr[r]));//比较minv与当前种类的杂交路线的时长的大小
    }
    if (minv != INF)  les[x] += minv;//如果当前的作物可以通过杂交获取
}
int main()
{
    int x, y, z;
    cin >> N >> M >> K >> T;
    for (int i = 1; i <= N; i++)
    {
        cin >> arr[i];
    }
    for (int i = 1; i <= M; i++)
    {
        cin >> x;
    }
    for (int i = 0; i < K; i++)
    {
        cin >> x >> y >> z;
        m[z].push_back({ x,y });
    }
    fill(les + 1, les + N + 1, -1);
    DFS(T);
    cout << les[T] << endl;
    return 0;
}

3  并查集

3.1  简介

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受;即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果，只能用并查集来描述。

并查集是一种树型的数据结构，用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。

3.2  模板

#include 
using namespace std;
const int maxn=5e3+10;
int n,m,p;
int fa[maxn];

int init()//初始化 
{
	for(int i=0;i>n>>m>>p;
	init();//初始化父节点； 
	int u,v;
	while(m--)
	{
		cin>>u>>v;
		merge(u,v);
	}
	while(p--)
	{
		cin>>u>>v;
		u=find(u);
		v=find(v);
		puts(u==v?"Yes":"No");
	}
}

3.3  例题

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

小蓝要用七段码数码管来表示一种特殊的文字。

上图给出了七段码数码管的一个图示，数码管中一共有 77 段可以发光的二 极管，分别标记为 a, b, c, d, e, f, g

小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符 的表达时，要求所有发光的二极管是连成一片的。

例如：b发光，其他二极管不发光可以用来表达一种字符。

例如 c发光，其他二极管不发光可以用来表达一种字符。这种方案与上 一行的方案可以用来表示不同的字符，尽管看上去比较相似。

例如：a, b, c, d, e 发光，f, g不发光可以用来表达一种字符。

例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光 的二极管没有连成一片。

请问，小蓝可以用七段码数码管表达多少种不同的字符？

方法：并查集+DFS

DFS用来枚举每一种情况，并查集用来检查边界

#include
using namespace std;
const int N = 10;
int use[N], ans, e[N][N], fa[N];

int find(int x)
{
	while (fa[x] != x) x = fa[x];
	return fa[x];
}

void merge(int a,int b)
{
	a=find(a);
	b=find(b);
	if(a!=b)
	{
		fa[b]=a;//结合到一起，也可以是fa[a]=b;
	}
}

void dfs(int d)
{
	if(d ==8)
	{
		/* 并查集判是否在同一集合 */
		for(int i = 1;i <= 7;i++)  fa[i] = i;//初始化父亲集合
		for(int i = 1;i <= 7;i++)
		{
			for(int j = 1;j <= 7;j++)
			{
				if(e[i][j] && use[i] && use[j])
				{
					merge(i,j);
				}
			}
		}	
		int k = 0;
		for(int i = 1;i <= 7;i++)
		{
			if(use[i] && fa[i] == i) k++;
		}
		if(k == 1) ans++;//如果所有亮灯都属于同一个集合
		return;
	}
	use[d] = 1;//打开d这个灯，继续开关下一个灯
	dfs(d + 1);
	use[d] = 0;//关闭d这个灯，继续开关下一个灯
	dfs(d + 1);
}

int main()
{
	e[1][2] = e[1][6] = 1;
	e[2][1] = e[2][7] = e[2][3] = 1;
	e[3][2] = e[3][4] = e[3][7] = 1;
	e[4][3] = e[4][5] = 1;
	e[5][4] = e[5][6] = e[5][7] = 1;
	e[6][1] = e[6][5] = e[6][7] = 1;
	e[7][2] = e[7][3] = e[7][5] = e[7][6] = 1;
	dfs(1);
	cout << ans;
	return 0;
}

4  最小生成树（以后更新）