Apriori算法的python实现

最近学习了关联分析和用于寻找频繁项集的Apriori算法，做了一些笔记，并且来自己实现一下。

一、Apriori原理

首先需要了解几个基本概念：

项(item)： 每个item成为一个项，例如购物记录里的apple, banana, orange每一件不同的物品就是一个项。
项集： 一个或多个项的集合组成项集。
频繁项集： 出现次数大于某个阈值的项集，称为频繁项集。
事务(transaction)： 每一条记录称为一次事务，本质是一个项集，例如某一次购买的商品集合。

频繁项集的评估标准

1. 支持度(support)是A，B同时出现的次数占总事务数的百分比。
   $$support(A,B)=P(A\cap B)$$

2. 置信度(confidence)是已知A出现条件下B出现的概率。
   $$confidence(A\Rightarrow B)=P(B\mid A)=\frac{P(A\cap B)}{P(A)}$$

Apriori基本思想与原理

前提假设：频繁项集的所有非空子集也一定是频繁的。

步骤：

1. 找出频繁项集：

• 对每条记录进行排序，使得item按照字典序排列，防止出现（a,b）和（b,a）同一个项集出现两次的情况。
• 产生频繁一项集，即数据列表中的每个item

2. 由频繁项集产生强关联规则

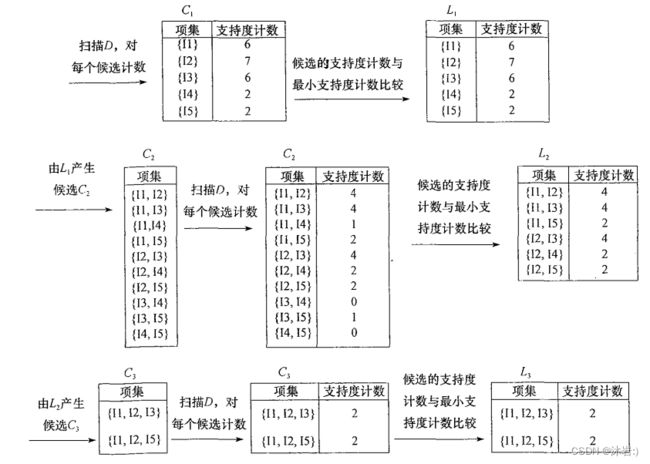
实际应用中很少直接采用Apriori算法，但基本都是对其改进后的算法。

二、评价

1. 缺点：

• 频繁一项集会很大
• 未考虑出现次数
• 应用于商业领域可能需要考虑能产生更高效益的频繁项集

2. 单纯频繁项集搜索及其改进算法比较成熟，但与推荐系统相结合仍然是值得探索的领域。

三、python实现Apriori算法

可惜的是，scikit-learn中并没有频繁集挖掘相关的算法类库，所以我自己编写python代码实现了一下这个算法。（借鉴了《数据挖掘》上提供的代码）

# 加载数据集，输出二维列表形式的数据
def load_data_set():
    data_set = [['l1', 'l2', 'l5'], ['l2', 'l4'], ['l2', 'l3'], ['l1', 'l2', 'l4'], ['l1', 'l3'], ['l2', 'l3'],
            ['l1', 'l3'], ['l1', 'l2', 'l3', 'l5'], ['l1', 'l2', 'l3']]
    return data_set

# 生成频繁一项集
def create_C1(data_set):
    C1 = set()
    for t in data_set:
        for item in t:
            item_set = frozenset([item])
            C1.add(item_set)
    return C1

# 判断是否满足apriori基本性质
def is_apriori(Ck_item, Lksub1):
    """
    Judge whether a frequent candidate k-itemset satisfy Apriori property.
    Args:
        Ck_item: a frequent candidate k-itemset in Ck which contains all frequent
                 candidate k-itemsets.
        Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
    Returns:
        True: satisfying Apriori property.
        False: Not satisfying Apriori property.
    """
    for item in Ck_item:
        sub_Ck = Ck_item - frozenset([item])
        if sub_Ck not in Lksub1:
            return False
    return True


def create_Ck(Lksub1, k):
    """
    Create Ck, a set which contains all all frequent candidate k-itemsets
    by Lk-1's own connection operation.
    Args:
        Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
        k: the item number of a frequent itemset.
    Return:
        Ck: a set which contains all all frequent candidate k-itemsets.
    """
    Ck = set()
    len_Lksub1 = len(Lksub1)
    list_Lksub1 = list(Lksub1)
    for i in range(len_Lksub1):
        for j in range(1, len_Lksub1):
            l1 = list(list_Lksub1[i])
            l2 = list(list_Lksub1[j])
            l1.sort()
            l2.sort()
            if l1[0:k-2] == l2[0:k-2]:
                Ck_item = list_Lksub1[i] | list_Lksub1[j]
                # pruning
                if is_apriori(Ck_item, Lksub1):
                    Ck.add(Ck_item)
    return Ck


def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):
    """
    Generate Lk by executing a delete policy from Ck.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
        Ck: A set which contains all all frequent candidate k-itemsets.
        min_support: The minimum support.
        support_data: A dictionary. The key is frequent itemset and the value is support.
    Returns:
        Lk: A set which contains all all frequent k-itemsets.
    """
    Lk = set()
    item_count = {}
    for t in data_set:
        for item in Ck:
            if item.issubset(t):
                if item not in item_count:
                    item_count[item] = 1
                else:
                    item_count[item] += 1
    t_num = float(len(data_set))
    for item in item_count:
        if (item_count[item] / t_num) >= min_support:
            Lk.add(item)
            support_data[item] = item_count[item] / t_num
    return Lk


def generate_L(data_set, k, min_support):
    """
    Generate all frequent itemsets.
    Args:
        data_set: A list of transactions. Each transaction contains several items.
        k: Maximum number of items for all frequent itemsets.
        min_support: The minimum support.
    Returns:
        L: The list of Lk.
        support_data: A dictionary. The key is frequent itemset and the value is support.
    """
    support_data = {}
    C1 = create_C1(data_set)
    L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
    Lksub1 = L1.copy()
    L = []
    L.append(Lksub1)
    for i in range(2, k+1):
        Ci = create_Ck(Lksub1, i)
        Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
        Lksub1 = Li.copy()
        L.append(Lksub1)
    return L, support_data


def generate_big_rules(L, support_data, min_conf):
    """
    Generate big rules from frequent itemsets.
    Args:
        L: The list of Lk.
        support_data: A dictionary. The key is frequent itemset and the value is support.
        min_conf: Minimal confidence.
    Returns:
        big_rule_list: A list which contains all big rules. Each big rule is represented
                       as a 3-tuple.
    """
    big_rule_list = []
    sub_set_list = []
    for i in range(0, len(L)):
        for freq_set in L[i]:
            for sub_set in sub_set_list:
                if sub_set.issubset(freq_set):
                    conf = support_data[freq_set] / support_data[freq_set - sub_set]
                    big_rule = (freq_set - sub_set, sub_set, conf)
                    if conf >= min_conf and big_rule not in big_rule_list:
                        # print freq_set-sub_set, " => ", sub_set, "conf: ", conf
                        big_rule_list.append(big_rule)
            sub_set_list.append(freq_set)
    return big_rule_list


if __name__ == "__main__":
    # Get the dataset in list format.
    data_set = load_data_set()
    
    # Do the iteration for n
    L, support_data = generate_L(data_set, k=3, min_support=0.2)
    
    # Get the frequent itemsets by given minimal confidence.
    big_rules_list = generate_big_rules(L, support_data, min_conf=0.7)
    
    # print the results
    for Lk in L:
        print("="*50)
        print("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport")
        print("="*50)
        for freq_set in Lk:
            print(freq_set, support_data[freq_set])
        print()
    print()
    print("Big Rules:")
    for item in big_rules_list:
        print(item[0], "=>", item[1], "confidence: ", item[2])
        

以上是以列表形式对数据进行处理，但对于大量样本数据，效率比较低下，而且机器学习模型标注数据集的格式是行表示记录，列表示特征，所以我想如果将列表数据转换成矩阵，然后通过对矩阵处理重新实现Apriori算法或许对于计算效率会有较大的提升。

参考文章

1. Apriori算法介绍（Python实现）