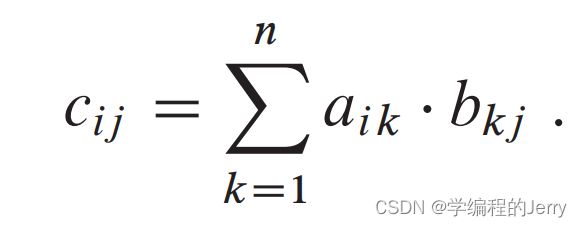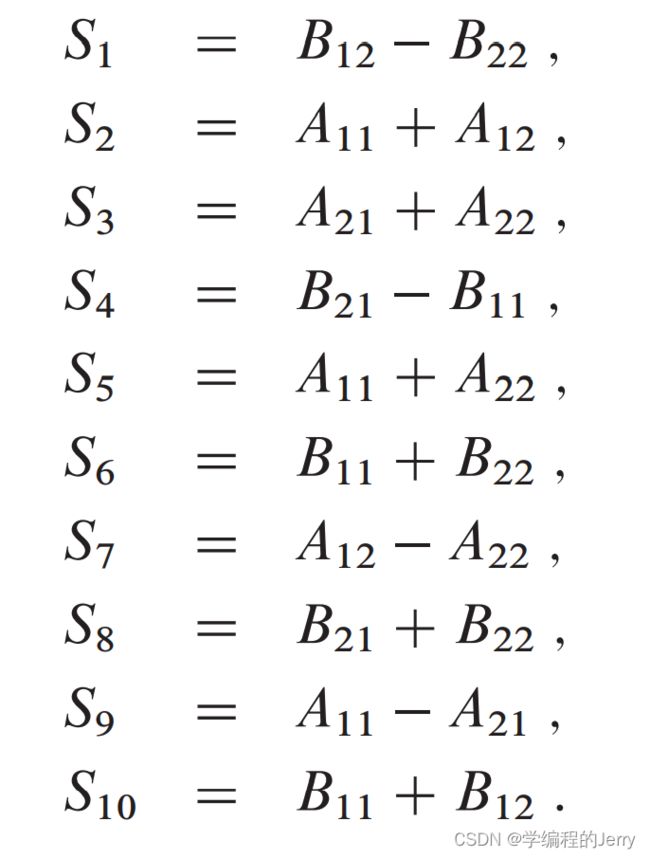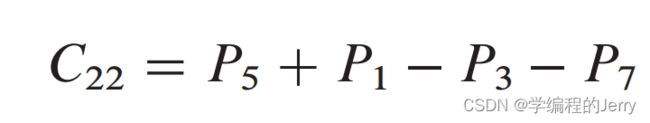《算法导论》第四章-矩阵乘法的Strassen算法(含C++代码)
一、引入与矩阵知识铺垫
这一章我们讲的主要是矩阵的乘法,在矩阵中假设C = A * B,其中的元素满足下面的规则
我们可以通过三重for循环实现矩阵的乘法,但是本章我们有更加方便的方法。
二、分治算法
1、初步思路
在矩阵C = A * B中,假设三个矩阵都是n * n的矩阵,且n为2的幂
我们将它们都分成四个n/2*n/2的矩阵:
其中
利用这些公式,我们可以直接写出递归分治算法的伪代码:
SQUARE-MATRIX-MULTIPLY-RECURSIVE(A,B)
1 n = A.rows //A的行数
2 let C be a new n*n matrix //让C变成新的n*n矩阵
3 if n == 1
4 c11 = a11 * b11
5 else partition A,B,and C as in equations //将三个矩阵各自分成4个部分
//分别求出四个元素
6 C11 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11,B11)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12,B21)
7 C12 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A11,B12)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A12,B22)
8 C21 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21,B11)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22,B21)
9 C22 = SQUARE-MATRIX-MULTIPLY-RECURSIVE(A21,B12)
+ SQUARE-MATRIX-MULTIPLY-RECURSIVE(A22,B22)
10 return C注意:第5行分解矩阵我们通过原矩阵一组行下标和一组列下标来表明新的子矩阵。
2、分析运行时间
①n=1,进行一次标量乘法,T(1) = Θ(1)
②n>1,使用下标分解矩阵花费Θ(1)时间;8次递归,每次递归需要调用完成两个n/2*n/2矩阵的乘法,因此花费的时间为8T(n/2)
③n>1,6~9行四次矩阵加法,每个矩阵n²/4个元素,因此需要花费Θ(n²)的时间
④n>1,通过下标计算将矩阵加法的结果放置在矩阵C 的正确位置上,花费Θ(1)的时间
最终得到以下结果
注意:虽然大多数时候渐近符号(Θ等)是包含了常数因子的,但是递归符号T(n/2)并不包含,因此8是必须提出来的。同时8也代表了递归树的茂盛,如果8没有写出来,这个递归就变成线性结构了(没有树枝)。
三、Strassen方法
1、引入
Strassen方法的递归树没有上面茂盛,它知识递归进行7次而非8次的n/2*n/2矩阵的乘法。
2、大致操作步骤
①将输入矩阵A、B和C分解成n/2*n/2的子矩阵。采用下标计算法,这个步骤花费θ(1)的时间,与SQUARE-MATRIX-MULTIPLY-RECURSIVE相同。
②创建10个n/2*n/2的矩阵S1、S2...S10,每个矩阵的保存步骤1中创建的两个子矩阵的和或差。因为该步骤必须进行10次n/2*n/2矩阵的加减法,因此花费的时间为θ(n²)。10个矩阵的计算方式如下:
③用步骤1中创建的子矩阵和步骤2中创建的10个矩阵,递归地计算7个矩阵积P1,P2...P7,且每个矩阵Pi都是n/2*n/2的。7个矩阵计算方式如下,我们只需要算红框部分就行了。
④通过Pi矩阵的不同组合进行加减运算,计算出结果矩阵C的子矩阵C11,C12,C21,C22,花费的时间为θ(n²)。其中

我们验证可以发现它们都是符合矩阵运算规律的
3、运行时间
n=1时,只需θ(1)的时间;n>1时,步骤1、2、4均花费θ(n²)的时间,步骤3进行了7次n/2*n/2矩阵的乘法,时间为7T(n/2),加起来从而得到
4、伪代码编写
Strassen()
let C be a new n*n matrix
if A.row == 1:
C = A * B
else partition A,B,and C //步骤1:将四个矩阵各自分为四部分
//步骤2:计算10个S
S1=B12-B22
S2=A11-A12
S3=A21+A22
S4=B21-B11
S5=A11+A22
S6=B11+B22
S7=A12-A22
S8=B21+B22
S9=A11-A21
S10=B11+B12
//步骤3:递归计算7个矩阵积
P1=Strassen(A11,S1)
P2=Strassen(A11,B22)
P3=Strassen(S3,B11)
P4=Strassen(A22,S4)
P5=Strassen(S5,S6)
P6=Strassen(S7,S8)
P7=Strassen(S9,S10)
//步骤4:不同Pi的加减运算
C11=P5+P4-P2+P6
C12=P1+P2
C21=P3+P4
C22=P5+P1-P3-P7
return C
C++代码
```cpp
#include
#include
using namespace std;
template
class Strassen_class {
public:
void ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize);
void SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize);
void MUL(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize);//朴素算法实现
void FillMatrix(T** MatrixA, T** MatrixB, int length);//A,B矩阵赋值
void PrintMatrix(T** MatrixA, int MatrixSize);//打印矩阵
void Strassen(int N, T** MatrixA, T** MatrixB, T** MatrixC);//Strassen算法实现
};
//矩阵相加
template
void Strassen_class::ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize)
{
for (int i = 0; i < MatrixSize; i++)
{
for (int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = MatrixA[i][j] + MatrixB[i][j];
}
}
}
//矩阵相减
template
void Strassen_class::SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize)
{
for (int i = 0; i < MatrixSize; i++)
{
for (int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = MatrixA[i][j] - MatrixB[i][j];
}
}
}
//普通的矩阵乘法
template
void Strassen_class::MUL(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize)
{
for (int i = 0; i < MatrixSize; i++)
{
for (int j = 0; j < MatrixSize; j++)
{
MatrixResult[i][j] = 0;
for (int k = 0; k < MatrixSize; k++)
{
MatrixResult[i][j] = MatrixResult[i][j] + MatrixA[i][k] * MatrixB[k][j];
}
}
}
}
//A、B矩阵赋值
template
void Strassen_class::FillMatrix(T** MatrixA, T** MatrixB, int length)
{
for (int row = 0; row < length; row++)
{
for (int column = 0; column < length; column++)
{
//给矩阵里赋值0到4的随机数
MatrixB[row][column] = (MatrixA[row][column] = rand() % 5);
}
}
}
//打印矩阵
template
void Strassen_class::PrintMatrix(T** MatrixA, int MatrixSize)
{
cout << endl;
for (int row = 0; row < MatrixSize; row++)
{
for (int column = 0; column < MatrixSize; column++)
{
cout << MatrixA[row][column] << "\t";
if ((column + 1) % ((MatrixSize)) == 0)
cout << endl;
}
}
cout << endl;
}
//Strassen算法
template
void Strassen_class::Strassen(int N, T * *MatrixA, T * *MatrixB, T * *MatrixC)
{
int HalfSize = N / 2;
int newSize = N / 2;
//当不能分成4个4*4的数组时,我们就采用正常的办法
if (N <= 64)
{
MUL(MatrixA, MatrixB, MatrixC, N);
}
else
{
//创建多个二维数组
T** A11; T** A12; T** A21; T** A22;
T** B11; T** B12; T** B21; T** B22;
T** C11; T** C12; T** C21; T** C22;
T** M1; T** M2; T** M3; T** M4;
T** M5; T** M6; T** M7;
T** AResult; T** BResult;
//创建一个一维数组的指针,用于寻找首地址
A11 = new T * [newSize];
A12 = new T * [newSize];
A21 = new T * [newSize];
A22 = new T * [newSize];
B11 = new T * [newSize];
B12 = new T * [newSize];
B21 = new T * [newSize];
B22 = new T * [newSize];
C11 = new T * [newSize];
C12 = new T * [newSize];
C21 = new T * [newSize];
C22 = new T * [newSize];
M1 = new T * [newSize];
M2 = new T * [newSize];
M3 = new T * [newSize];
M4 = new T * [newSize];
M5 = new T * [newSize];
M6 = new T * [newSize];
M7 = new T * [newSize];
AResult = new T * [newSize];
BResult = new T * [newSize];
int newLength = newSize; //N/2长度
//在上面一维数组的基础上,分别在每一行再创建一个一维数组的指针,从而实现一个二维数组
for (int i = 0; i < newSize; i++)
{
A11[i] = new T[newLength];
A12[i] = new T[newLength];
A21[i] = new T[newLength];
A22[i] = new T[newLength];
B11[i] = new T[newLength];
B12[i] = new T[newLength];
B21[i] = new T[newLength];
B22[i] = new T[newLength];
C11[i] = new T[newLength];
C12[i] = new T[newLength];
C21[i] = new T[newLength];
C22[i] = new T[newLength];
M1[i] = new T[newLength];
M2[i] = new T[newLength];
M3[i] = new T[newLength];
M4[i] = new T[newLength];
M5[i] = new T[newLength];
M6[i] = new T[newLength];
M7[i] = new T[newLength];
AResult[i] = new T[newLength];
BResult[i] = new T[newLength];
}
//将输入的数组四等分成N/2*N/2的数组,将A和B中的数组各自赋值给自己的四个分支数组
for (int i = 0; i < N / 2; i++)
{
for (int j = 0; j < N / 2; j++)
{
A11[i][j] = MatrixA[i][j];
A12[i][j] = MatrixA[i][j + N / 2];
A21[i][j] = MatrixA[i + N / 2][j];
A22[i][j] = MatrixA[i + N / 2][j + N / 2];
B11[i][j] = MatrixB[i][j];
B12[i][j] = MatrixB[i][j + N / 2];
B21[i][j] = MatrixB[i + N / 2][j];
B22[i][j] = MatrixB[i + N / 2][j + N / 2];
}
}
//计算7个矩阵
//M1=A11(B12-B22)
SUB(B12, B22, BResult, HalfSize);
Strassen(HalfSize, A11, BResult, M1);
//M2=(A11+A12)B22
ADD(A11, A12, AResult, HalfSize);
Strassen(HalfSize, AResult, B22, M2);
//M3=(A21+A22)B11
ADD(A21, A22, AResult, HalfSize);
Strassen(HalfSize, AResult, B11, M3);
//M4=A22(B21-B11)
SUB(B21, B11, BResult, HalfSize);
Strassen(HalfSize, A22, BResult, M4);
//M5=(A11+A22)(B11+B22)
ADD(A11, A22, AResult, HalfSize);
ADD(B11, B22, BResult, HalfSize);
Strassen(HalfSize, AResult, BResult, M5);
//M6=(A12-A22)(B21+B22)
SUB(A12, A22, AResult, HalfSize);
ADD(B21, B22, BResult, HalfSize);
Strassen(HalfSize, AResult, BResult, M6);
//M7=(A11-A21)(B11+B12)
SUB(A11, A21, AResult, HalfSize);
ADD(B11, B12, BResult, HalfSize);
Strassen(HalfSize, AResult, BResult, M6);
//C11 = M5 + M4 - M2 + M6;
ADD(M5, M4, AResult, HalfSize);
SUB(M6, M2, BResult, HalfSize);
ADD(AResult, BResult, C11, HalfSize);
//C12 = M1 + M1;
ADD(M1, M2, C12, HalfSize);
//C21 = M3 + M4;
ADD(M3, M4, C21, HalfSize);
//C22 = M5 + M1 - M3 - M7;
ADD(M5, M1, AResult, HalfSize);
ADD(M7, M3, BResult, HalfSize);
SUB(AResult, BResult, C22, HalfSize);
//组合小矩阵到一个大矩阵
for (int i = 0; i < N / 2; i++)
{
for (int j = 0; j < N / 2; j++)
{
MatrixC[i][j] = C11[i][j];
MatrixC[i][j + N / 2] = C12[i][j];
MatrixC[i + N / 2][j] = C21[i][j];
MatrixC[i + N / 2][j + N / 2] = C22[i][j];
}
}
// 释放矩阵内存空间
for (int i = 0; i < newLength; i++)
{
delete[] A11[i]; delete[] A12[i]; delete[] A21[i];delete[] A22[i];
delete[] B11[i]; delete[] B12[i]; delete[] B21[i];delete[] B22[i];
delete[] C11[i]; delete[] C12[i]; delete[] C21[i];delete[] C22[i];
delete[] M1[i]; delete[] M2[i]; delete[] M3[i]; delete[] M4[i];
delete[] M5[i]; delete[] M6[i]; delete[] M7[i];
delete[] AResult[i]; delete[] BResult[i];
}
delete[] A11; delete[] A12; delete[] A21; delete[] A22;
delete[] B11; delete[] B12; delete[] B21; delete[] B22;
delete[] C11; delete[] C12; delete[] C21; delete[] C22;
delete[] M1; delete[] M2; delete[] M3; delete[] M4;
delete[] M5;delete[] M6; delete[] M7;
delete[] AResult;delete[] BResult;
}
}
int main()
{
Strassen_class stra;//定义Strassen_class类对象
int MatrixSize = 0;
int** MatrixA; //存放矩阵A
int** MatrixB; //存放矩阵B
int** MatrixC; //存放结果矩阵
cout << "\n请输入矩阵大小(必须是2的幂指数值(例如:32,64,512,..): ";
cin >> MatrixSize;
int N = MatrixSize;//for readiblity.
//申请内存
MatrixA = new int* [MatrixSize];
MatrixB = new int* [MatrixSize];
MatrixC = new int* [MatrixSize];
//申请空间
for (int i = 0; i < MatrixSize; i++)
{
MatrixA[i] = new int[MatrixSize];
MatrixB[i] = new int[MatrixSize];
MatrixC[i] = new int[MatrixSize];
}
stra.FillMatrix(MatrixA, MatrixB, MatrixSize); //矩阵赋值
stra.Strassen(N, MatrixA, MatrixB, MatrixC); //strassen矩阵相乘算法
cout << "\n矩阵运算结果... \n";
stra.PrintMatrix(MatrixC, MatrixSize);
return 0;
}