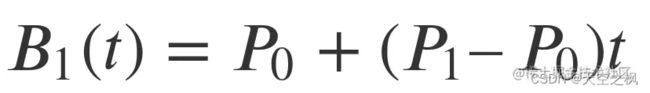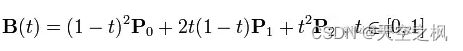贝赛尔曲线
贝赛尔曲线的定义:
贝赛尔曲线是应用于二维图形程序的数学曲线,曲线定义:起始点,终止点(也称锚点),控制点.通过调整控制点,贝赛尔曲线的形状会发生变化.
线性贝赛尔曲线:数学公式
由于这个是线性变化,所以满足我们数学公式y = kx+b ,其中k代表的是斜率,因为P1和P0都是向量,所以向量的相减的数学意义其实是两个点之间的斜率
二阶贝赛尔曲线:
首先我们要明白一个道理,n阶的贝赛尔曲线对应的是n-1个控制点,二阶贝赛尔曲线是如何画出平滑的曲线?
我们在P0P1线段上找到一个点A,然后以相同比例在P1P2找一个B,连接AB这条直线,同样在AB上同比例的点C,不断重复上面过程,就得到这条曲线了,
即(P0A/P0P1) = (AC/AB) = (P1B/P1P2)
//Path 与曲线
path元素的形状是通过属性`[d](https://developer.mozilla.org/zh-CN/docs/Web/SVG/Attribute/d)`定义的,属性d的值是一个“命令+参数”的序列,我们将讲解这些可用的命令,并且展示一些示例。
M x y
M 表示Move to 的简写,简单点讲就是移动画笔到路径的起点位置,后面的x,y就是起点的坐标,并不会画出图形
L x y
L 就是Line to 就是画出一条直线,L命令将会在当前位置和新位置之间画一条线段
H x
V y
H 绘制水平线,V绘制垂直线.这两个命令都只带一个参数,标明在x轴或y轴移动的位置,因为他们都只在坐标轴的一个方向上移动.H 20 表示前面画笔所在的点的y不变,x的位置加 20这两个点之间画一条直线.V 20 就是x不变,y增加20.
Z or z
Z 就是路径闭合.命令会当前点画一条直线到路径的起点.
接下来我们就用path 实操一下 画一个正方形
对应的path 代码如下:
接下来我们就进入曲线的一些属性
Q x1 y1,x yQ 表示二阶贝赛尔曲线 x1,y1,就是二阶贝赛尔曲线的控制点,x,y是曲线的终点,曲线的起点是由画笔的上一的点构成,这就形出二阶贝赛尔曲线
那么如果我们想画连续的二阶贝赛尔曲线?
T x y
T 的这个属性 必须跟在Q的后面 如果单独使用 直接画多个T 就是一条直线
T x y 表示下一段贝赛尔曲线的终点,他会自动根据前一个控制点,去推断
三阶贝赛尔曲线
C x1 y1 x2 y2,x y
三阶贝赛尔曲线 用表示x1 y1,x2 y2 表示两个端点x,y表示两个端点x,y表示贝赛尔曲线的终点,同样的我如果想画出连续的曲线呢?这时候就需要用S这个参数了
S x2 y2,x y
S x2,y2 表示第二个控制点,x,y表示终点.那么它的第一个控制点会被假设成前一个命令曲线的第二个控制点的中心对称点
弧线
A rx ry x-axis-rotation large-arc-flag sweep-flag x y
椭圆弧顾名思义有长轴和短轴,ok rx,ry就表示长轴半径和短轴半径 x-axis-rotation顾名思义就是x轴旋转角度,这个怎么去理解
large-arc-flag 决定弧线
canvas进阶——贝塞尔公式推导与物体跟随复杂曲线的轨迹运动 - 个人文章 - SegmentFault 思否