Python中的统计学（二）

大数定律和中心极限定律都是概率论中重要的定理。它们之间的不同在于它们所涉及的随机变量和极限的不同。

大数定律是指随着样本容量的增大，样本均值越来越接近于总体均值的定律。即样本均值的极限等于总体均值，也就是说，当样本量足够大时，样本均值可以很好地反映总体均值。

中心极限定理是指当样本量趋近于无限大时，样本均值的分布趋近于正态分布。换句话说，对于任何一种分布，只要样本容量足够大，那么它的样本均值分布就可以近似地看作是正态分布，且这个近似程度随着样本容量的增大而增加。

简单来说，大数定律告诉我们，随着样本量的增大，样本均值越来越接近总体均值；而中心极限定理则告诉我们，对于任何一种分布，只要样本容量足够大，样本均值就可以看作是正态分布，且这个近似程度随着样本容量的增大而增加。

大数定律的python实现：

import random
import matplotlib.pyplot as plt

# 掷骰子模拟函数
def roll_dice():
    return random.randint(1, 6)

# 大数定律模拟函数
def law_of_large_numbers(num_samples):
    # 用于保存每次模拟的平均值
    means = []
    
    for i in range(1, num_samples + 1):
        # 模拟投掷 i 次骰子并计算平均值
        values = [roll_dice() for j in range(i)]
        mean = sum(values) / i
        
        # 将当前平均值加入列表
        means.append(mean)
    
    # 绘制平均值随样本数量变化的折线图
    plt.plot(list(range(1, num_samples + 1)), means)
    plt.xlabel("Number of samples")
    plt.ylabel("Mean value")
    plt.title("Law of Large Numbers")
    plt.show()

# 测试
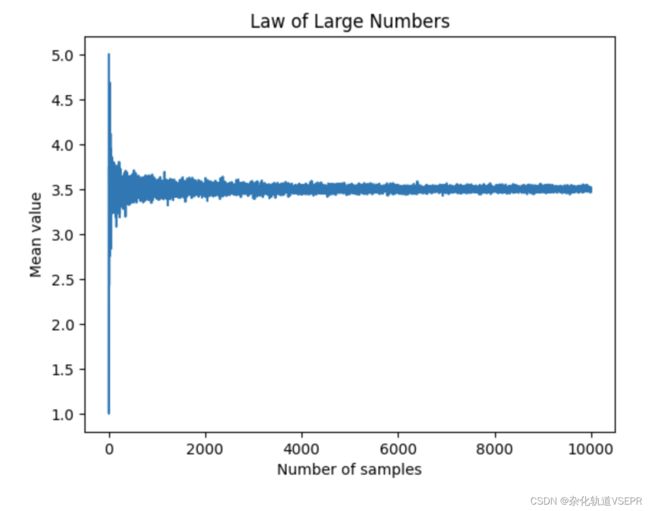
law_of_large_numbers(1000)

它生成的图像如下所示：

中心极限定律的实现：

import numpy as np
import matplotlib.pyplot as plt

# 生成一些随机变量
samples = np.random.rand(1000, 100)

# 计算每行的和
sums = np.sum(samples, axis=1)

# 绘制直方图
plt.hist(sums, bins=50, density=True, alpha=0.7, color='skyblue')

# 绘制正态分布曲线
mean = np.mean(sums)
std = np.std(sums)
x = np.linspace(mean - 4 * std, mean + 4 * std, 100)
y = 1 / (std * np.sqrt(2 * np.pi)) * np.exp(-0.5 * ((x - mean) / std) ** 2)
plt.plot(x, y, color='red')

# 显示图像
plt.show()

F分布

F分布（F-distribution）是一种连续概率分布，常用于比较两个样本方差是否显著不同。F分布有两个自由度参数：$d_1$ 和 $d_2$，通常用于计算两个随机变量的方差比值的概率分布。

在 Python 中，可以使用 SciPy 库中的 f 模块来生成 F 分布随机变量、计算概率密度函数和累积分布函数等。以下是一个生成 F 分布随机变量并绘制其概率密度函数的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f

# 设置 F 分布的自由度参数
dfn, dfd = 10, 20

# 生成 F 分布随机变量
rvs = f.rvs(dfn=dfn, dfd=dfd, size=10000)

# 绘制 F 分布的概率密度函数
x = np.linspace(0, 5, 100)
pdf = f.pdf(x, dfn=dfn, dfd=dfd)
plt.plot(x, pdf, label='F-distribution')

# 显示图像
plt.legend()
plt.show()

图示如下：

卡方分布

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2

# 设定自由度参数 k
k = 3

# 生成一组卡方分布的随机样本
samples = chi2.rvs(k, size=1000)

# 绘制卡方分布的概率密度函数图像
x = np.linspace(0, 20, 1000)
y = chi2.pdf(x, k)
plt.plot(x, y, linewidth=2, color='blue')

# 绘制随机样本的直方图
n, bins, patches = plt.hist(samples, bins=50, density=True, alpha=0.7, color='skyblue')

plt.title('Chi-Square Distribution')
plt.xlabel('x')
plt.ylabel('Probability density')

plt.show()

T分布

简称 t 分布，在概率论及统计学中用于根据小样本来估计总体呈正态分布且标准差未知的期望值。若总体标准差已知，或是样本数足够大时依据中心极限定理渐进正态分布则应使用正态分布来进行估计。

from scipy.stats import t

# 设置自由度和均值
df = 10
mean = 0

# 生成一组 T 分布随机变量
samples = t.rvs(df=df, loc=mean, size=1000)

# 计算概率密度函数
pdf = t.pdf(x=samples, df=df, loc=mean)

# 绘制概率密度函数图像
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(samples, pdf)
ax.set_xlabel('X')
ax.set_ylabel('PDF(X)')
ax.set_title(f'T-distribution with df={df} and mean={mean}')
plt.show()

指数分布

指数分布具有无记忆性，它可以用来表示独立随机事件的发生间隔

import numpy as np
import matplotlib.pyplot as plt

# 生成一组指数分布的随机样本
lam = 0.5  # 指数分布的参数 lambda
sample_size = 1000
samples = np.random.exponential(1/lam, size=sample_size)

# 绘制样本的直方图和理论的概率密度函数曲线
fig, ax = plt.subplots()
n, bins, patches = ax.hist(samples, bins=50, density=True, alpha=0.7, color='skyblue')

# 计算指数分布的概率密度函数
x = np.linspace(0, np.max(samples), 1000)
pdf = lam * np.exp(-lam * x)

# 绘制理论的概率密度函数曲线
ax.plot(x, pdf, 'r', linewidth=2)

# 设置图表标题和轴标签
ax.set_title("Exponential Distribution (lambda=0.5)")
ax.set_xlabel("Values")
ax.set_ylabel("Probability Density")

# 显示图表
plt.show()