PyTorch深度学习实战 | 高斯混合模型聚类原理分析
01、问题描述
为理解高斯混合模型解决聚类问题的原理,本实例采用三个一元高斯函数混合构成原始数据,再采用GMM来聚类。
1) 数据
三个一元高斯组件函数可以采用均值和协方差表示如表1所示:
▍表1 三个一元高斯组件函数的均值和协方差
每个高斯组件函数分配不同的权重,其中1号组件权重为30%, 2号组件权重为50%,3号组件权重为20%,随机生成1000个样本数据。
2) 可视化
为了理解三个高斯组件函数是如何混合的,可以将三个一元高斯函数显示在二维坐标中,显示三个高斯组件函数的钟形图。然后,三个组件按照权重比率混合,显示三个组件函数混合后的图形。
3) 聚类
为了找到混合后的数据属于哪一个组件,可以采用聚类的方法来对数据分类。聚类后给每个数据分配1,2或者3其中的一个标签,回顾在混合三个高斯函数时的顺序,对于1000个样本数据,是否对应前300个属于1号组件,正确标签应该为1,中间500个属于2号组件,正确标签应该为2,最后200个属于3号组件,正确标签应该为3,查看聚类后得到分类标签的准确率。
02、实例分析参考解决方案
数据生成MATLAB/Octave参考代码:
mu1=[-1];
mu2=[0];
mu3=[3];
sigma1=[2.25];
sigma2=[1];
sigma3=[.25];每个高斯组件函数分配不同的权重,其中1号组件权重为30%, 2号组件权重为50%,3号组件权重为20%,随机生成1000个样本数据,MATLAB代码如下所示:
weight1=[.3];
weight2=[.5];
weight3=[.2];
component_1=mvnrnd(mu1,sigma1,300);
component_2=mvnrnd(mu2,sigma2,500);
component_3=mvnrnd(mu3,sigma3,200);
X=[component_1;component_2;component_3];三个一元高斯函数显示在二维坐标中,MATLAB代码如下所示:
gd1=exp(-0.5*((component_1-mu1)/sigma1).^2)/(sigma1*sqrt(2*pi));
gd2=exp(-0.5*((component_2-mu2)/sigma2).^2)/(sigma2*sqrt(2*pi));
gd3=exp(-0.5*((component_3-mu3)/sigma3).^2)/(sigma3*sqrt(2*pi));
figure;
plot(component_1,gd1,'.');hold on;
plot(component_2,gd2,'.');hold on;
plot(component_3,gd3,'.');
title('Bell cureves of three components');
xlabel('Randomly produced numbers');ylabel('Gauss distribution');运行以上代码后,可看到三个组件函数的钟形图如图1所示。
▍图1 三个一元高斯函数的钟形图
三个组件按照权重比率混合,MATLAB代码如下所示:
gm1=gmdistribution.fit(X,3);
a=pdf(gm1,X);
figure;plot(X,a,'.');
title('Curve of Gaussian mixture distribution');
xlabel('Randomly produced numbers');
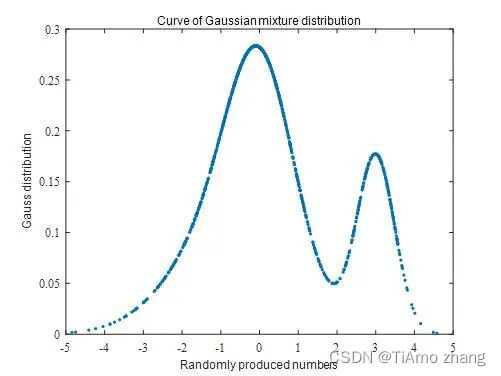
ylabel('Gauss distribution');运行以上代码,获得三个组件混合后的图形如图2所示。
▍图2 三个一元高斯函数混合后的图形
为了找到混合后的数据属于哪一个组件,可以采用聚类的方法来对数据分类,MATLAB实现代码如下:
idx=cluster(gm1,X);聚类后给每个数据分配1,2或者3其中的一个标签,回顾在混合三个高斯函数时的顺序,对于1000个样本数据,前300个属于1号组件,正确标签应该为1,中间500个属于2号组件,正确标签应该为2,最后200个属于3号组件,正确标签应该为3,聚类结果后得到分类标签的准确率可以采用如下代码来查看:
figure;
hold on;
for i=1:1000
ifidx(i)==1
plot(X(i),0,'r*');
elseifidx(i)==2
plot(X(i),0,'b+');
else
plot(X(i),0,'go');
end
end
title('Plot illustrating the cluster assignment');
xlabel('Randomly produced numbers');
ylim([-0.1 0.1]);03、运行结果
运行代码聚类结果如图3所示,可以看出,绝大部分的数据被分配到正确的标签,也存在少数错误分类。
▍图3 高斯混合模型聚类结果分析
04、代码
https://www.jianguoyun.com/p/Ddr2dTYQ9of0Chiko_4EIAA
05、文末送书
内容简介
Web3正频繁出现在公众视野中,然而受阻于晦涩难懂的技术原理及陌生又拗口的专业术语,很多人对此望而却步。本书试图用通俗的语言、简单的结构、翔实的案例让零基础的读者迅速掌握Web3的核心要义。
Web3不仅仅是技术和金融语境,它和每个人的生活都息息相关。作为深耕Web3的研究机构,Inverse DAO将带你通过纵向时间线、横向技术线来立体、客观、完整地理解Web3。通过本书你既可以快速读懂行业,也可以躬身实践参与。
希望本书可以抛砖引玉,启迪你的智慧之光,发现Web3更多、更广、更深的奥秘,助你在新的科技浪潮下,无往而不胜。
作者简介
Anymose,中国人民大学传播学硕士,Inverse DAO(Web3投资研究机构)发起人,曾供职知名风险资本分析师,具有丰富的Web3理论研究、项目投资、运营实践经验,帮助Qredo、Fetch、Gitcoin等诸多项目进行新一代信息化建设。
参与方式:文章三连并评论“珍爱生命,远离加班”,参与抽奖,送出2本技术图书《从零开始读懂Web3》,24小时后,公布抽奖结果!