对红黑树的认识及TreeMap对应实现-学习记录
文章目录
- 1 概述
-
- 1.1 红黑树的定义
-
- 红黑规则
- 1.2 红黑树的引入
-
- 什么是二叉查找树?
- 二叉搜索树和平衡二叉树的区别?
- 平衡二叉树和红黑树的区别?
- 什么是不严格的平衡?
- 2 红黑树的基本原理
-
- 2.1 常用函数
-
- 获取相关参数
- 比较函数
- 2.2 旋转调整
-
- 2.2.1 左旋
- 2.2.2 右旋
- 3 插入节点
-
- 3.1 基础插入操作
- 3.2 插入平衡调整
-
- 情况一:父亲和叔叔都是红色节点
- 情况二:叔叔节点不为红色,且祖父-父亲-关注节点共线
- 情况三:叔叔节点不为红色,且祖父-父亲-关注节点不共线
- 4 删除节点
-
- 4.1 基础删除操作
-
- 情况一:待删除节点只有一个子节点
- 情况二:待删除元素的左右子节点都存在
- 情况三:待删除元素是叶子节点
- 情况四:待删除元素是根节点
- 4.2 删除平衡调整
-
- 情况一:兄弟为红色节点
- 情况二:兄弟及其左右子节点均为黑色节点
- 情况三:兄弟为黑色节点,其左子节点为红色
- 情况四:兄弟为黑色节点,其右子节点为红色
- 5 参考文章
1 概述
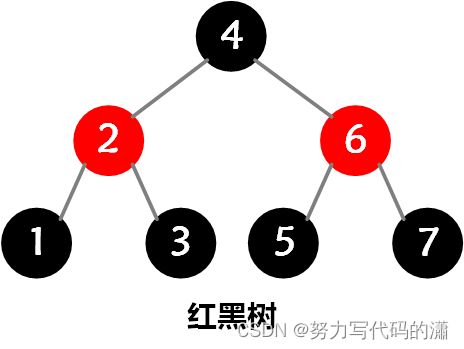
1.1 红黑树的定义
红黑规则
- 任何一个节点都有颜色,黑色或者红色。根节点一定是黑色的。
- 每个叶子节点都是黑色的空节点(
NIL),叶子节点不存储数据。 - 任何相邻的节点都不能同时为红色。
- 任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等。
注意:
- 在下文中,将黑色的、空的叶子节点都省略掉了
1.2 红黑树的引入
什么是二叉查找树?
- 二叉查找树(
Binary Search Tree,简称BST)是一棵二叉树,它的左子节点的值比父节点的值要小,右节点的值要比父节点的值大。它的高度决定了它的查找效率。 - 在理想的情况下,二叉查找树增删查改的时间复杂度为 O ( l o g 2 N ) O(log_{2}{N}) O(log2N)(其中N为节点数),最坏的情况下为 O ( N ) O(N) O(N)。
- 当它的高度为 l o g 2 N + 1 log_{2}{N}+1 log2N+1时,我们就说二叉查找树是平衡的。
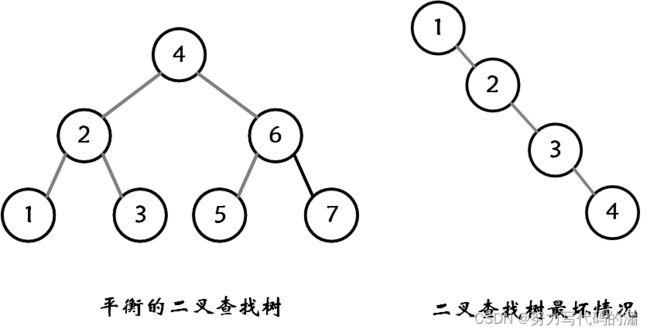
二叉搜索树和平衡二叉树的区别?
二叉搜索树:
- 容易退化成一条链
- 查找的时间复杂度从 O ( l o g 2 N ) O(log_{2}{N}) O(log2N) 退化成 O ( N ) O(N) O(N)
平衡二叉树:
- 左右子树高度差有限制
- 保证查找操作的最坏时间复杂度也为 O ( l o g 2 N ) O(log_{2}{N}) O(log2N)
平衡二叉树和红黑树的区别?
平衡二叉树AVL:
- 左右子树高度差不能超过1,每次进行插入/删除操作时,几乎都需要通过旋转操作保持平衡
- 在频繁进行插入/删除的场景中,频繁的旋转操作使得AVL的性能大打折扣
红黑树:
- 红黑树通过牺牲严格的平衡,换取插入/删除时少量的旋转操作,整体性能优于
AVL- 红黑树插入时的不平衡,不超过两次旋转就可以解决;删除时的不平衡,不超过三次旋转就能解决
- 红黑树的红黑规则,保证最坏的情况下,也能在 O ( l o g 2 N ) O(log_{2}{N}) O(log2N)时间内完成查找操作。
什么是不严格的平衡?
- 一棵极其平衡的二叉树(满二叉树或完全二叉树)的高度大约是 l o g 2 N log_{2}{N} log2N
- 所以如果要证明红黑树是近似平衡的,只需要分析,红黑树的高度是否比较稳定地趋近 l o g 2 N log_{2}{N} log2N
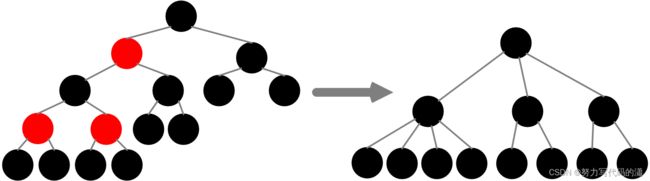
去除红黑树中的红色节点:
-
红色节点删除之后,有些节点就没有父节点了,它们会直接拿这些节点的祖父节点(父节点的父节点)作为父节点。所以,之前的二叉树就变成了四叉树。
-
从四叉树中取出某些节点,放到叶节点位置,四叉树就变成了完全二叉树。所以,仅包含黑色节点的四叉树的高度,比包含相同节点个数的完全二叉树的高度还要小。
-
完全二叉树的高度近似 l o g 2 N log_{2}{N} log2N,这里的四叉“黑树”的高度要低于完全二叉树,所以去掉红色节点的“黑树”的高度也不会超过 l o g 2 N log_{2}{N} log2N。
-
假设某条查询路径上的红色节点为
N个,则黑色节点之至少有N个(根节点必须为黑色节点)- 路径中没有红色节点的,路径高度为: l o g 2 N log_{2}{N} log2N
- 路径中红色节点达到最大值是,路径高度不超过: 2 ∗ l o g 2 N 2 * log_{2}{N} 2∗log2N
-
最坏情况下红黑树的高度只比高度平衡的
AVL树的高度仅仅大了一倍,在性能上,下降得并不多。推导出来的结果不够精确,实际上红黑树的性能更好。
2 红黑树的基本原理
- 下述原理的代码实现均取自
TreeMap的源码 - 红黑树应该在每次插入、删除操作之后保证自身结构满足红黑树的四条规则
- 在插入、删除节点的过程中,第三、第四点要求可能会被破坏,而“平衡调整”实际上就是要把被破坏的第三、第四点恢复过来。
2.1 常用函数
获取相关参数
/* 获取节点颜色 */
private static <K,V> boolean colorOf(Entry<K,V> p) {
return (p == null ? BLACK : p.color);
}
/* 设置节点颜色 */
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
if (p != null)
p.color = c;
}
/* 获取节点的父节点 */
private static <K,V> Entry<K,V> parentOf(Entry<K,V> p) {
return (p == null ? null: p.parent);
}
/* 获取节点的左子节点 */
private static <K,V> Entry<K,V> leftOf(Entry<K,V> p) {
return (p == null) ? null: p.left;
}
/* 获取节点的右子节点 */
private static <K,V> Entry<K,V> rightOf(Entry<K,V> p) {
return (p == null) ? null: p.right;
}
比较函数
/* 通过自定义比较器或内置比较器比较元素大小 */
final int compare(Object k1, Object k2) {
return comparator==null ? ((Comparable<? super K>)k1).compareTo((K)k2)
: comparator.compare((K)k1, (K)k2);
}
2.2 旋转调整
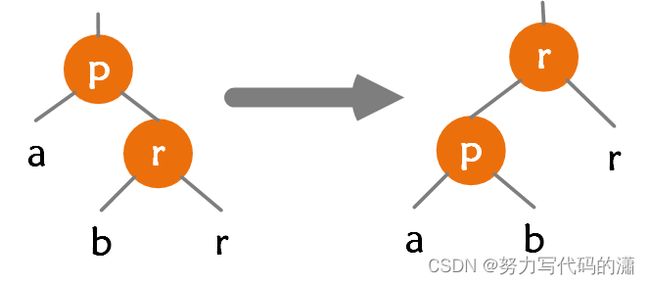
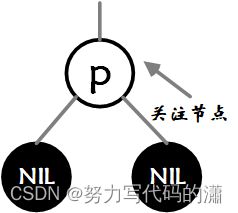
- 图中的
a / b / r可以为子树、元素、空元素NIL - 围绕父节点
p的转动
2.2.1 左旋
TreeMap源码
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right;
/* 将 r 的左子节点 交给 p 的右子节点 */
p.right = r.left;
if (r.left != null)
r.left.parent = p;
/* 将 r 和 p 的父节点更新 */
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
/* p 变成 r 的左子节点*/
r.left = p;
p.parent = r;
}
}
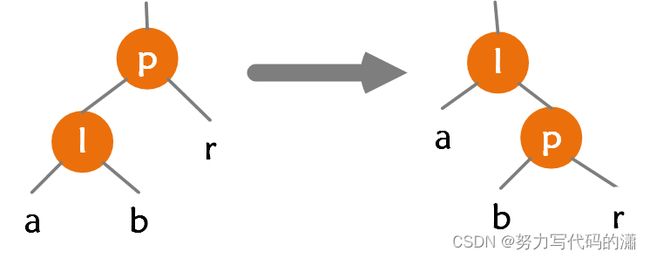
2.2.2 右旋
TreeMap源码
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
3 插入节点
-
红黑树的平衡调整过程是一个向root节点回溯迭代的过程,当关注节点符合红黑树定义或到达根节点,平衡调整结束
-
关注节点:正在处理的节点。关注节点会随着不停地迭代处理,而不断发生变化
- 插入操作中的初始关注节点就是插入节点
-
本文以左子树举例,右子树为镜像操作
-
红黑树规定,插入的节点必须是红色的。而且,二叉查找树中新插入的节点都是放在叶子节点上。
-
为了简化描述,把父节点的兄弟节点叫作叔叔节点,父节点的父节点叫作祖父节点。
3.1 基础插入操作
- 基础插入操作就是将节点根据大小在红黑树中指定叶子节点位置创建新节点,并设置为红色
- 将新建节点设置为关注节点,执行平衡调整操作
TreeMap源码:
- 根据是否声明比较器进行节点的定位及节点创建
- 如果插入的节点是根节点,那我们直接改变它的颜色,无须进入平衡调整操作
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
3.2 插入平衡调整
- 平衡调整迭代的终止条件:
- 关注节点为根节点
- 关注节点的父节点是黑色的
- 调整中的基础操作:左旋、右旋、改变颜色
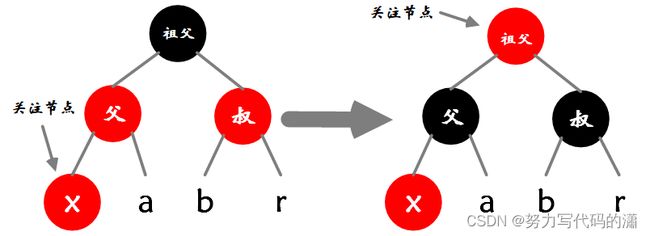
情况一:父亲和叔叔都是红色节点
- 示例情况:关注节点是父节点的左子节点。
- 对称情况:关注节点是父节点的右子节点,处理方法相同
- 图中的
a / b / r可以为子树、元素、空元素NIL
处理方法:
-
更改叔、父颜色为黑色、祖父颜色为红色(满足条件三:任何相邻的节点都不能同时为红色。)
-
同时,在以祖父节点为根节点的子树中,所有叶子节点到达祖父节点经过的黑色节点数不变(满足条件四:任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等。)
-
由于对祖父节点进行了改色处理,但又不知道祖父节点的父节点是否为红色(不一定满足条件三)
-
仅截取左子节点情况下的处理方法
/* 迭代终止条件 */
while (x != null && x != root && x.parent.color == RED) {
/* 父节点是祖父节点的左子节点 */
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
/* 判断叔、父节点都为红色 */
if (colorOf(y) == RED) {
/* 重置 父、叔、祖父 节点的颜色 */
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
/* 设置关注节点为父节点 */
x = parentOf(parentOf(x));
}
}
}
情况二:叔叔节点不为红色,且祖父-父亲-关注节点共线
- 叔叔节点不为红色:叔叔节点可以不存在,或者为黑色节点。如果为红色则属于情况一
- 祖父-父亲-关注节点共线:三个节点在一条斜线上
- 示例情况:父亲节点是祖父节点的左子节点,关注节点是父亲节点的左子节点
- 对称情况:父亲节点是祖父节点的右子节点,关注节点是父亲节点的右子节点
处理方法:
-
更改父节点颜色为黑色,祖父节点颜色为红色(满足条件三:任何相邻的节点都不能同时为红色。)
-
对祖父节点执行右旋操作,提升父亲节点,将父亲节点的右子节点变成祖父节点的左子节点,旋转后,各叶子节点到达当前子树根节点经过的黑色节点数不变(满足条件四:任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等。)
-
操作结束后,不存在不满足条件的节点,迭代结束
TreeMap中相关处理代码
- 情况二与情况三的处理代码相联系,请先阅读情况三
情况三:叔叔节点不为红色,且祖父-父亲-关注节点不共线
- 叔叔节点不为红色:叔叔节点可以不存在,或者为黑色节点。如果为红色则属于情况一
- 祖父-父亲-关注节点共线:三个节点在一条斜线上
- 示例情况:父亲节点是祖父节点的左子节点,关注节点是父亲节点的左子节点
- 对称情况:父亲节点是祖父节点的右子节点,关注节点是父亲节点的右子节点
处理方法:
- 对父节点进行一次左旋操作,使祖父-父亲-关注节点共线,进入情况二
TreeMap中相关处理代码
- 截取对称情况
/* 迭代终止条件 */
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
} else { /* 父节点是祖父节点的右子节点 */
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
} else { /* 叔 节点的颜色不为红色 */
/* 情况二:如果不共线,则进行一次旋转操作,并更改关注节点 */
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
/* 情况二:共线的祖父-父亲-关注节点 旋转祖父节点,执行颜色改变*/
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
4 删除节点
-
删除操作首先需要做的也是
BST的删除操作,删除操作会删除对应的节点- 如果是叶子节点就直接删除
- 如果是非叶子节点,会用对应的中序遍历的后继节点来顶替要删除节点的位置。
-
红黑树的平衡调整过程是一个向root节点回溯迭代的过程,当关注节点符合红黑树定义或到达根节点,平衡调整结束
区分:
-
关注节点
r:正在处理的节点。关注节点会随着不停地迭代处理,而不断发生变化 -
待删除节点
p:删除操作执行前,节点中key与要删除的key值相等的节点 -
删除操作开始时,初始关注节点的位置与具体情况有关,并不与待删除节点恒相等
注意:
-
本文以左子树举例,右子树为镜像操作
-
为了简化描述,把父节点的兄弟节点叫作叔叔节点,父节点的父节点叫作祖父节点。
4.1 基础删除操作
- 通过
getEntry(key)函数,找待删除节点的位置
情况一:待删除节点只有一个子节点
- 直接删除
P节点,将r节点设置为关注节点,进入平衡调整操作
TreeMap中相关处理代码
private void deleteEntry(Entry<K,V> p) {
/* 如果左右子节点都存在,需要特殊处理 */
if (p.left != null && p.right != null) {
}
/* r 指针指向待删除节点p的唯一子节点 */
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/* 确实存在唯一子节点 */
if (replacement != null) {
/* 执行删除 p 节点操作 */
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
/* 确保不会影响GC回收 */
p.left = p.right = p.parent = null;
/* 进入平衡调整的条件,后续会讲 */
if (p.color == BLACK)
fixAfterDeletion(replacement);
}
}
情况二:待删除元素的左右子节点都存在
-
使用待删除元素中序遍历的后续元素的
key & value值更改待删除元素节点,不改变树的结构,仅做值的更改 -
后继元素一定没有左子节点,否则其不是待删除元素中序遍历的后继节点(可证明)
-
将后继元素标记为待删除元素,在基础删除操作中重新匹配情况
TreeMap中相关处理代码
private void deleteEntry(Entry<K,V> p) {
/* 当待删除元素的左右子树都存在时,找到其后继元素,替换值,重新标记为待删除元素 */
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
}
情况三:待删除元素是叶子节点
- 将当前叶子节点标记为关注节点
- 先平衡,后删除(与其他情况有所不同)
private void deleteEntry(Entry<K,V> p) {
/* 定位到待删除元素一个非空的子节点 */
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
} else if (p.parent == null) {
}
/* 左右子节点均为空,说明为叶子节点 */
else {
/* 删除前需要执行平衡调整操作 */
if (p.color == BLACK)
fixAfterDeletion(p);
/* 如果平衡调整后节点不是根节点,执行删除操作 */
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
情况四:待删除元素是根节点
- 直接执行删除操作,无须进入平衡调整
TreeMap中相关处理代码
private void deleteEntry(Entry<K,V> p) {
/* 如果左右子节点都存在,需要特殊处理 */
if (p.left != null && p.right != null) {
}
/* r 指针指向待删除节点p的唯一子节点 */
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/* 确实存在唯一子节点 */
if (replacement != null) {
}
/* 待删除节点为根节点 */
else if (p.parent == null) {
root = null;
} else {
}
}
4.2 删除平衡调整
平衡调整迭代的终止条件(修复完成):
-
关注节点是
root节点时- 退出并保证其一定为黑色
-
关注节点是红色节点
- 说明以关注节点为根节点的子树的黑色路径长度均少1
- 将节点颜色更改为黑色,红黑树(满足条件四:任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等。)
关注节点的含义(个人理解):
-
黑色路径长度:我们定义,在一个红黑树中,叶子节点到其根节点经过的黑色节点数为
-
以图为例,待删除节点为
2节点- 删除前,每个
NIL的黑色路径长度均为2 - 删除节点后,左侧两个叶子节点黑色路径长度为1(不满足条件四:任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等。)
- 将节点
6更改为红色,使树中每个叶子节点的黑色路径长度均为1
- 删除前,每个
-
在以关注节点为根节点的子树中,所有的叶子节点的黑色路径长度缺少1(相较于关注节点的兄弟节点)
-
平衡调整:解决上述问题,在删除元素后,解决关注节点为根节点的子树中,叶子结点的黑色路径长度少1的问题
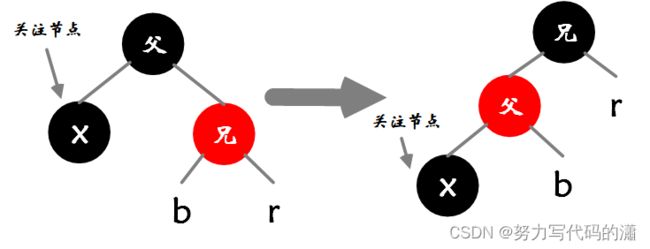
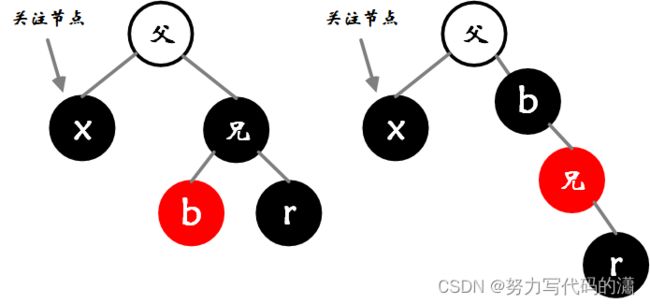
情况一:兄弟为红色节点
- 示例情况:关注节点是父节点的左子节点。
- 对称情况:关注节点是父节点的右子节点,执行相反操作
- 图中的
b / r可以为子树、元素、空元素NIL
处理方法:
- 兄弟节点中存在可以借用的红色节点
- 对父节点执行左旋 / 右旋操作,关注节点不变,继续选择情况处理
TreeMap中相关处理代码
private void fixAfterDeletion(Entry<K,V> x) {
/* 迭代终止条件 */
while (x != root && colorOf(x) == BLACK) {
/* 关注节点是左子节点 */
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
/* 兄弟节点为红色 */
if (colorOf(sib) == RED) {
/* 更改颜色 */
setColor(sib, BLACK);
setColor(parentOf(x), RED);
/* 执行一次左旋操作 */
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/* 继续选择情况处理 */
if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) {
} else {
}
}
}
/* 设置根节点,或者颜色为红色的关注节点为黑色 */
setColor(x, BLACK);
}
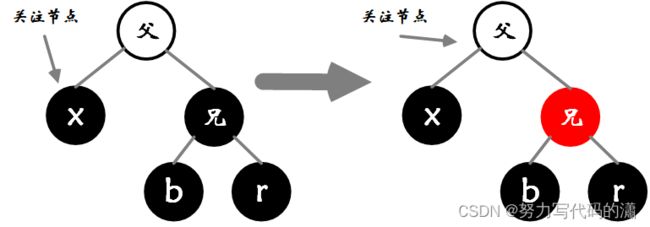
情况二:兄弟及其左右子节点均为黑色节点
- 示例情况:关注节点是父节点的左子节点。
- 对称情况:关注节点是父节点的右子节点,执行相反操作
- 图中的
b / r可以为子树、元素、空元素NIL
处理方法:
- 以关注节点为根节点的子树黑色路径长度均少1
- 右侧兄弟节点可以变为红色,使以兄弟节点为根节点的子树黑色路径长度少1
- 改色之后,以父节点为根节点的子树的黑色路径长度少1,将其设置为关注节点,迭代调整
TreeMap中相关处理代码
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
}
/* 兄弟及其子节点均为黑色节点 */
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
/* 调整关注节点,进入迭代 */
x = parentOf(x);
}
}
}
setColor(x, BLACK);
}
情况三:兄弟为黑色节点,其左子节点为红色
- 示例情况:关注节点是父节点的左子节点。
- 对称情况:关注节点是父节点的右子节点,执行相反操作
- 图中的
b / r可以为子树、元素、空元素NIL
处理方法:
- 对兄弟节点执行一次右旋操作,使红色节点成为新兄弟节点的右子节点
- 保持关注节点不变,进入迭代(情况四)
TreeMap中相关处理代码
- 情况三与情况四的处理代码相联系,请先阅读情况四
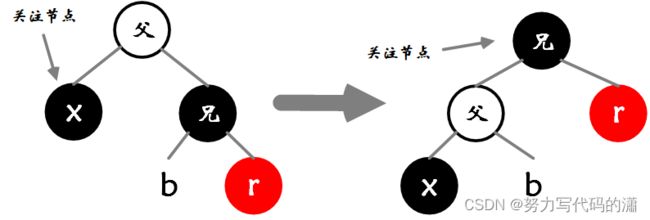
情况四:兄弟为黑色节点,其右子节点为红色
- 示例情况:关注节点是父节点的左子节点。
- 对称情况:关注节点是父节点的右子节点,执行相反操作
- 图中的
b / r可以为子树、元素、空元素NIL
处理方法:
- 对父节点执行左旋操作,使黑色的兄弟节点能够使关注节点子树的黑色路径高度加1
- 关注节点指向兄弟节点,不满足迭代条件,退出循环
TreeMap中相关处理代码
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(leftOf(sib)) == BLACK &&colorOf(rightOf(sib)) == BLACK) {
}
/* 子节点中一定存在一个红色节点 */
else {
/* 如果兄弟节点的右子节点为黑色,说明左子节点为红色 */
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
/* 对兄弟节点执行右旋,使兄弟节点的右节点为红色 */
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/* 对父节点执行一次左旋操作,平衡操作结束 */
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
5 参考文章
-
对红黑树的认识总结_张彦峰ZYF的博客-CSDN博客
-
红黑树深入剖析及Java实现 - 美团技术团队 (meituan.com)
-
红黑树详解_晓之木初的博客-CSDN博客_红黑树