简单控制知识了解（pid+简单滑模）

---

一、PID控制

PID(proportion integration differentiation)其实就是指比例，积分，微分控制，指用误差信号控制被控量

控制算法公式:
$$u(t)=k_p(err(t)+\frac{1}{T_1}{\int }_0^{1}err(t)\mathrm{d}x+\frac{T_{D}derr(t)}{dt})$$
离散形式：
$$u(k)=k_p(e(k)+\frac{T}{T_1}\sum _{n=0}^{k}e(k)+\frac{T_D}{T}(e(k)-e(k-1))$$
输入：例如电机转速的预定值
输出：电机的转速的实际值
误差：输入-输出
比例项：误差乘比例系数，叠加到输入中，从而控制系统的输出，存在稳态误差（例：小车在接近终点时，误差较小，输入较小，不足以抵抗外界（例如摩擦力）影响，小车在接近终点时静止了，即稳态误差）
积分项：对误差积分（累加），增大输入，以消除稳态误差
微分项：负数项（误差必然越来越小），当误差极具减小，输入应当放缓。能够减小震荡。

二、PID控制算法实现

1.位置式PID

控制算法公式:
$$u(k)=k_{p}e(k)+k_i\sum _{n=0}^{k}e(k)+k_d(e(k)-e(k-1))$$

#include
using namespace std;

class PID
{
public:
    PID();
    float SetSpeed;           //定义设定值
    float ActualSpeed;        //定义实际值
    float err;                //定义偏差值
    float err_last;           //定义上一个偏差值
    float Kp, Ki, Kd;         //定义比例、积分、微分系数
    float voltage;            //定义电压值（控制执行器的变量）
    float integral;           //定义积分值
};
PID::PID()//构造函数初始化
{
    SetSpeed=0.0;
    ActualSpeed=0.0;
    err=0.0;
    err_last=0.0;
    Kp = 0.2;
    Ki = 0.015; 
    Kd = 0.2;
    integral = 0.0;
}
float PID_realize(PID &pid, float speed) {
    pid.SetSpeed = speed;
    pid.err = pid.SetSpeed - pid.ActualSpeed;
    pid.integral += pid.err;
    pid.voltage = pid.Kp * pid.err + pid.Ki * pid.integral + pid.Kd * (pid.err - pid.err_last);
    pid.err_last = pid.err;
    pid.ActualSpeed = pid.voltage * 1.0;
    return pid.ActualSpeed;
}
int main() {
    printf("System begin \n");
    PID pid;
    int count = 0;
    while (count < 1000)
    {
        float speed = PID_realize(pid,200.0);
        printf("%f\n", speed);
        count++;
    }
    return 0;
}

2.增量式PID

控制算法公式:
$$△u(k)=u(k)-u(k-1)$$
$$△u(k)=k_p(e(k)-e(k-1))+k_{i}e(k)+k_d(e(k)-2e(k-1)+e(k-2))$$
参数确定的情况下，只和最近三次的偏差有关，与位置式相比，增量式计算量小很多

#include
using namespace std;

class PID
{
public:
    PID();
    float SetSpeed;            //定义设定值
    float ActualSpeed;        //定义实际值
    float err;                //定义偏差值
    float err_next;            //定义上一个偏差值
    float err_last;            //定义最上前的偏差值
    float Kp, Ki, Kd;            //定义比例、积分、微分系数
};
PID::PID()//构造函数初始化
{
    SetSpeed=0.0;
    ActualSpeed=0.0;
    err=0.0;
    err_last=0.0;
    err_next = 0.0;
    Kp = 0.2;
    Ki = 0.015; 
    Kd = 0.2;

}
float PID_realize(PID &pid, float speed) 
{

    pid.SetSpeed = speed;
    pid.err = pid.SetSpeed - pid.ActualSpeed;
    float incrementSpeed=pid.Kp*(pid.err-pid.err_next)+pid.Ki*pid.err+pid.Kd*(pid.err-2*pid.err_next+pid.err_last);
    pid.err_last = pid.err_next;
    pid.err_next = pid.err;
    pid.ActualSpeed += incrementSpeed;
    return pid.ActualSpeed;

}
int main() {
    printf("System begin \n");
    PID pid;
    int count = 0;
    while (count < 1000)
    {
        float speed = PID_realize(pid,200.0);
        printf("%f\n", speed);
        count++;
    }
    return 0;
}

参考博客（优缺点总结）

二、简单的滑模控制

1.系统描述

负载通过电机控制输入u来控制，动态模型如下：
$$J\ddot{\theta }=u+d(t)$$
其中$\theta (t)$是角位置；$J>0$为转动惯量；$d(t)$为干扰项且满足$|d(t)|\le \eta$;$\eta$为干扰上界。取位置指令为常数值${\theta }_d(t)$,$err=\theta -{\theta }_d$为跟踪误差

1.滑模控制律设计

控制的目的是在$u(t)$输出下，使得$err=0,\dot{err}=0$,定义跟踪误差函数s为
$$s=cerr+\dot{err},c>0$$
若$s=0$,解微分方程
$$cerr+\dot{err}=0⟹\{\begin{array}{l}\dot{err}=-c\dot{err}(0)e^{-ct},\\ err=err(0)e^{-ct},\end{array}$$
状态量会以指数速度最终趋于0，s=0即滑模面。在方程$s=cerr+\dot{err},c>0$中引入u,对其求导得(输入为阶跃响应的情况下)
$$\dot{s}=c(\dot{\theta }-\dot{{\theta }_d})+\ddot{\theta }-\ddot{{\theta }_d}=c\dot{\theta }+\frac{1}{J}(u+d(t)),c>0$$

对于关于s的状态方程，如何保证s=0（即s=0是平衡点，满足渐近稳定性）,根据Lyapunov稳定判定的第二方法，如果存在一个连续函数V满足

  $(1)$   $V(0)=0$
  $(2)$   $V(x)>0$  $x!=0$
  $(3)$   $\dot{V}(x)<0$  $x!=0$
那么系统将在平衡点$s=0$ 稳定，即${\lim }_{t\to \infty }s(t)=0$
令$V=\frac{1}{2}{s}^2$,明显满足（1）（2）条件,对于第三个条件
$$\dot{V}(x)=\dot{s}s$$
趋近律就是指的$\dot{s}$（趋近律是为了使 s收敛到0，例如，$s>0$时，$\dot{s}<0$，那么$s$就会收敛到0。滑模运动包括趋近运动和滑模运动两个过程。趋近运动为s→0的过程，滑模运动即$err\to 0,\dot{err}\to 0$的过程。趋近律一般有如下几种设计：

对于$\dot{s}=-\epsilon sgn(s)-ks$,令
$$u=J(-c\dot{\theta }-\frac{1}{J}(\eta sgn(s)+ks))$$
带入
$$\dot{V}=s(c\dot{\theta }+\frac{1}{J}(u+d(t)))$$
得
$$\dot{V}=\frac{1}{J}(-k{s}^2-\eta |s|+sd(t))\le -\frac{1}{J}k{s}^2$$
满足条件(3),则即s=0是平衡点，满足渐近稳定性。

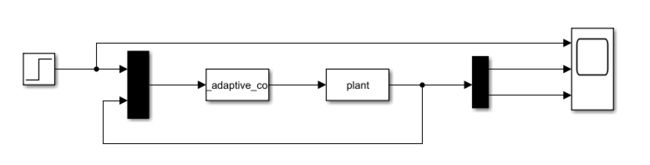
1.程序设计

控制器代码

function [sys,x0,str,ts] = simple_adaptive_controller(t, x, u, flag)
switch flag,
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;  % 调用初始化子函数
  case 1,
    sys=[];
  case 2,
    sys=[];
  case 3,
    sys=mdlOutputs(t,x,u);    %计算输出子函数
  case 4,
    sys=[];   %计算下一仿真时刻子函数
  case 9,
    sys=[];    %终止仿真子函数
  otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
 
end
 
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes   %初始化子函数
 
sizes = simsizes;
 
sizes.NumContStates  = 0;  %连续状态变量个数
sizes.NumDiscStates  = 0;  %离散状态变量个数
sizes.NumOutputs     = 1;  %输出变量个数
sizes.NumInputs      = 3;   %输入变量个数
sizes.DirFeedthrough = 1;   %输入信号是否在输出端出现
sizes.NumSampleTimes = 0;   % at least one sample time is needed
 
sys = simsizes(sizes);
x0  = [];   %初始值
str = [];   
ts  = [];   %[0 0]用于连续系统，[-1 0]表示继承其前的采样时间设置
simStateCompliance = 'UnknownSimState';
 
function sys=mdlOutputs(t,x,u)   %计算输出子函数
 
J = 2;
thd = u(1);
th = u(2);
dth = u(3);
 
e = th - thd;
de = dth;
c = 10;
s = c*e + de;
xite = 1.1;
 
k = 0;
ut = J*(-c*dth-1/J*(k*s+xite*sign(s)));
sys(1) = ut;

受控对象代码（干扰为sint）

function [sys,x0,str,ts] = plant(t, x, u, flag)
switch flag,
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;  % 调用初始化子函数
  case 1,
    sys=mdlDerivatives(t,x,u);   %调用计算微分子函数
  case 2,
    sys=[];
  case 3,
    sys=mdlOutputs(t,x,u);    %计算输出子函数
  case 4,
    sys=[];   %计算下一仿真时刻子函数
  case 9,
    sys=[];    %终止仿真子函数
  otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
 
end
 
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes   %初始化子函数
 
sizes = simsizes;
 
sizes.NumContStates  = 2;  %连续状态变量个数
sizes.NumDiscStates  = 0;  %离散状态变量个数
sizes.NumOutputs     = 2;  %输出变量个数
sizes.NumInputs      = 1;   %输入变量个数
sizes.DirFeedthrough = 0;   %输入信号是否在输出端出现
sizes.NumSampleTimes = 1;   % at least one sample time is needed
 
sys = simsizes(sizes);
x0  = [0, 0];   %初始值
str = [];   
ts  = [0 0];   %[0 0]用于连续系统，[-1 0]表示继承其前的采样时间设置
simStateCompliance = 'UnknownSimState';
 
function sys = mdlDerivatives(t, x, u)    %计算微分子函数，微分方程求解
J = 2;
dt = sin(t);
ut = u(1);
sys(1) = x(2);
sys(2) = 1/J*(ut+dt);
 
function sys=mdlOutputs(t,x,u)   %计算输出子函数
sys(1) = x(1);
sys(2) = x(2);

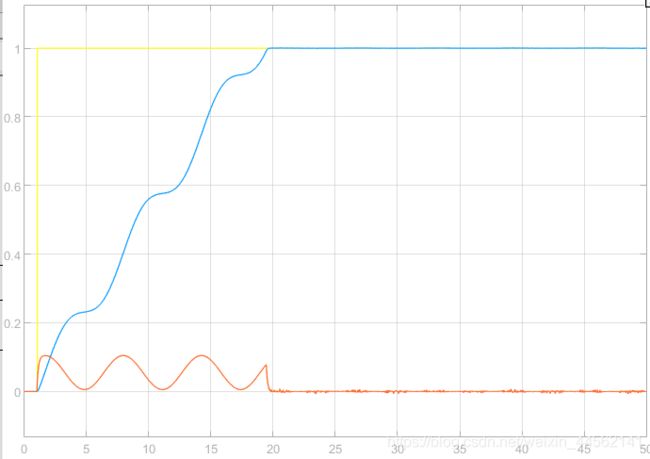
参考：
【控制理论】滑模控制最强解析
滑模控制程序及Simulink仿真
滑模控制自学笔记
Matlab S函数 function sys=mdlDerivatives(t,x,u)
【Matlab】简单的滑模控制程序及Simulink仿真
滑模变结构控制MATLAB仿真-基本理论与设计方法,刘金琨著