Timus1132(二次剩余方程求解)
题目：http://acm.timus.ru/problem.aspx?space=1&num=1132
题意：就是给出方程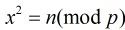
，p为素数，求在区间
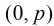内的解。
这个思路很简单，详见：http://algo.ftiasch.com/tag/number-theory/
一开始TLE，原因是我用了二分加法，以后记住：二分加法是适合很大数的，比较小的数就直接乘，不然数据多了可能TLE。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <math.h>
using namespace std;
typedef long long LL;
LL quick_mod(LL a,LL b,LL m)
{
LL ans=1;
a%=m;
while(b)
{
if(b&1)
{
ans=ans*a%m;
b--;
}
b>>=1;
a=a*a%m;
}
return ans;
}
struct T
{
LL p,d;
};
LL w;
//二次域乘法
T multi_er(T a,T b,LL m)
{
T ans;
ans.p=(a.p*b.p%m+a.d*b.d%m*w%m)%m;
ans.d=(a.p*b.d%m+a.d*b.p%m)%m;
return ans;
}
//二次域上快速幂
T power(T a,LL b,LL m)
{
T ans;
ans.p=1;
ans.d=0;
while(b)
{
if(b&1)
{
ans=multi_er(ans,a,m);
b--;
}
b>>=1;
a=multi_er(a,a,m);
}
return ans;
}
//求勒让德符号
LL Legendre(LL a,LL p)
{
return quick_mod(a,(p-1)>>1,p);
}
LL mod(LL a,LL m)
{
a%=m;
if(a<0) a+=m;
return a;
}
LL Solve(LL n,LL p)
{
if(p==2) return 1;
if (Legendre(n,p)+1==p)
return -1;
LL a=-1,t;
while(true)
{
a=rand()%p;
t=a*a-n;
w=mod(t,p);
if(Legendre(w,p)+1==p) break;
}
T tmp;
tmp.p=a;
tmp.d=1;
T ans=power(tmp,(p+1)>>1,p);
return ans.p;
}
int main()
{
int t,p,n,a,b;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&p);
n%=p;
a=Solve(n,p);
if(a==-1)
{
puts("No root");
continue;
}
b=p-a;
if(a>b) swap(a,b);
if(a==b)
printf("%d\n",a);
else
printf("%d %d\n",a,b);
}
return 0;
}