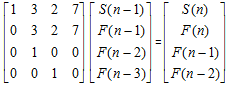FZU oj 1683 纪念SlingShot(矩阵快速幂)

http://acm.fzu.edu.cn/problem.php?pid=1683

自己独立完成的矩阵快速幂，O(∩_∩)O哈哈~

Description

已知 F（n）=3 * F（n-1）+2 * F（n-2）+7 * F（n-3），n>=3，其中F（0）=1，F（1）=3，F（2）=5，对于给定的每个n，输出F（0）+ F（1）+ …… + F（n） mod 2009。

Input

第一行是一整数m，代表总共有m个cases。

Output

对于每个case，输出一行。格式见样例，冒号后有一个空格。

Sample Input

2
3
6

Sample Output

Case 1: 37
Case 2: 313
此题采用矩阵快速幂
题意：f(0)=1,f(1)=3,f(2)=5,f(n)=3f(n-1)+2f(n-2)+5f(n-3)。求s(n)=(f(0)+f(1)……+f(n))%2009。
思路：S(n)=S(n-1)+F(n)=S(n-1)+3F(n-1)+2F(n-2)+7F(n-3)，因此构造矩阵：
我从s3开始使用矩阵，  从S0就开始用矩阵，想出来太麻烦，就干脆直接从S3吧
AC代码
#include <cstdio>
using namespace std;
#define N 4
#define MOD 2009
void matric_mul(int a[][N], int b[][N])
{
	int i, j, k;
	int tmp1[N][N] = {0};

	for (i = 0; i < N; i++)
	{
		for (j = 0; j < N; j++)
		{
			for (k = 0; k < N; k++)
			{
				tmp1[i][j] = (tmp1[i][j] + b[i][k] * a[k][j]) % MOD;
			}
		}
	}

	for (i = 0; i < N; i++)
	{
		for (j = 0; j < N; j++)
		{
			a[i][j] = tmp1[i][j];
		}
	}
}
int quickpow(int n)
{
	//int ans=1,tmp=base;
	//int ans[4][4] = {{1, 0, 0, 0}, {0, 1, 0, 0},{0, 0, 1, 0},{0, 0, 0, 1}};
	int tmp[4][4] = {{1, 3, 2, 7}, {0, 3, 2, 7},{0, 1, 0, 0},{0, 0, 1, 0}};
	int begin[4][4] = {{9, 0, 0, 0},{5, 0, 0, 0},{3, 0, 0, 0},{1, 0, 0, 0}};

	while (n)
	{
		if (n & 1)
		{
			matric_mul(begin,tmp);
		}			//ans=(ans*tmp)%MOD;tmp=(tmp*tmp)%MOD;

		matric_mul(tmp, tmp);

		n >>= 1;
	}

	return begin[0][0];
}
int main()
{
	int t,k = 1;
	scanf("%d",&t);
	while (t--)
	{
		int n;
		scanf("%d",&n);
		printf("Case %d: ",k++);
		if(n>2)
			printf("%d\n", quickpow(n-2));
		else
		{
			if(n==0) printf("1\n");
			else if(n==1)  printf("4\n");
			else printf("9\n");
		}
	}

	return 0;
}