（Problem 53）Combinatoric selections

There are exactly ten ways of selecting three from five, 12345:

123, 124, 125, 134, 135, 145, 234, 235, 245, and 345

In combinatorics, we use the notation, ⁵C₃ = 10.

In general,

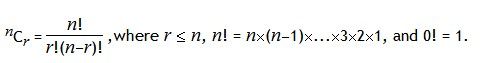
It is not until n = 23, that a value exceeds one-million: ²³C₁₀ = 1144066.

How many, not necessarily distinct, values of  ⁿC_r, for 1  n  100, are greater than one-million?

题目大意：

从五个数12345中选出三个数一共有十种方法:

123, 124, 125, 134, 135, 145, 234, 235, 245, and 345

在组合数学中我们用⁵C₃ = 10来表示.

n = 23时产生第一个超过一百万的数: ²³C₁₀ = 1144066.

对于ⁿC_r,  1  n  100，有多少超过100万的值？包括重复的在内。

//（Problem 53）Combinatoric selections

// Completed on Fri, 14 Feb 2014, 07:20

// Language: C11

//

// 版权所有（C）acutus   (mail: [email protected]) 

// 博客地址：http://www.cnblogs.com/acutus/



#include<stdio.h>

#include<math.h>



long long combinatoric(int n, int r)   //计算组合数的函数

{

    int i;

    long long s = 1;

    if(r > n / 2) r = n - r;

    for(i = n; i >= n - r + 1; i--) {

        s *= i;

    }

    for(i = 1; i <= r; i++) {

        s /= i;

    }

    return s;

}



int main()

{

    int i, j, s;

    s = 0;

    for(i = 23; i <= 100; i++) {

        j = 3;

        while(combinatoric(i, j) < 1000000) j++;

        if(i % 2) {

            s += (i / 2 - j + 1) * 2;   //利用组合数的对称性，分奇偶两种情况

        } else {

            s += (i / 2 - j) * 2 + 1;

        }

    }

    printf("%d\n", s);

    return 0;

}

Answer:

4075