zoj 1010 Area【线段相交问题】
链接:
Jerry, a middle school student, addicts himself to mathematical research. Maybe the problems he has thought are really too easy to an expert. But as an amateur, especially as a 15-year-old boy, he had done very well. He is so rolling in thinking the mathematical problem that he is easily to try to solve every problem he met in a mathematical way. One day, he found a piece of paper on the desk. His younger sister, Mary, a four-year-old girl, had drawn some lines. But those lines formed a special kind of concave polygon by accident as Fig. 1 shows.
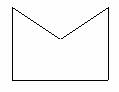
Fig. 1 The lines his sister had drawn
"Great!" he thought, "The polygon seems so regular. I had just learned how to calculate the area of triangle, rectangle and circle. I'm sure I can find out how to calculate the area of this figure." And so he did. First of all, he marked the vertexes in the polygon with their coordinates as Fig. 2 shows. And then he found the result--0.75 effortless.
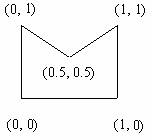
Fig.2 The polygon with the coordinates of vertexes
Of course, he was not satisfied with the solution of such an easy problem. "Mmm, if there's a random polygon on the paper, then how can I calculate the area?" he asked himself. Till then, he hadn't found out the general rules on calculating the area of a random polygon. He clearly knew that the answer to this question is out of his competence. So he asked you, an erudite expert, to offer him help. The kind behavior would be highly appreciated by him.
Input
The input data consists of several figures. The first line of the input for each figure contains a single integer n, the number of vertexes in the figure. (0 <= n <= 1000).
In the following n lines, each contain a pair of real numbers, which describes the coordinates of the vertexes, (xi, yi). The figure in each test case starts from the first vertex to the second one, then from the second to the third, ���� and so on. At last, it closes from the nth vertex to the first one.
The input ends with an empty figure (n = 0). And this figure not be processed.
Output
As shown below, the output of each figure should contain the figure number and a colon followed by the area of the figure or the string "Impossible".
If the figure is a polygon, compute its area (accurate to two fractional digits). According to the input vertexes, if they cannot form a polygon (that is, one line intersects with another which shouldn't be adjoined with it, for example, in a figure with four lines, the first line intersects with the third one), just display "Impossible", indicating the figure can't be a polygon. If the amount of the vertexes is not enough to form a closed polygon, the output message should be "Impossible" either.
Print a blank line between each test cases.
Sample Input
5
0 0
0 1
0.5 0.5
1 1
1 0
4
0 0
0 1
1 0
1 1
0
Output for the Sample Input
Figure 1: 0.75
Figure 2: Impossible
Source: Asia 2001, Shanghai (Mainland China)
算法:计算几何 线段相交问题 面积问题
题意 + 思路:
分析:
// = 0 表示,相交于端点也是认定为相交
bool SegmentProperIntersection(Point s1, Point e1, Point s2, Point e2) {
double c1 = Cross(s2-s1, e1-s1), c2 = Cross(e1-s1, e2-s1),
c3 = Cross(s1-s2, e2-s2), c4 = Cross(e2-s2, e1-s2);
if(c1*c2 >= 0 && c3*c4 >= 0) return true;
return false;
}
//叉积求面积 ,下标从 0 开始
double Area() {
double area = 0;
for(int i = 1; i < n-1; i++)
area += Cross(p[i]-p[0], p[i+1]-p[0]);
return fabs(area) / 2.0;
}
code:
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<iostream>
using namespace std;
const int maxn = 1000+10;
int n;
struct Point{
double x,y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
Point operator - (const Point &b) const{
return Point(x-b.x, y-b.y);
}
}p[maxn];
double Cross(Point a, Point b) { //叉积
return a.x*b.y - a.y*b.x;
}
// = 0 表示,相交于端点也是认定为相交
bool SegmentProperIntersection(Point s1, Point e1, Point s2, Point e2) {
double c1 = Cross(s2-s1, e1-s1), c2 = Cross(e1-s1, e2-s1),
c3 = Cross(s1-s2, e2-s2), c4 = Cross(e2-s2, e1-s2);
if(c1*c2 >= 0 && c3*c4 >= 0) return true;
return false;
}
bool haveCross() {
//从第 三 条线段开始, 一直到第 N-1 条线段
for(int i = 2; i < n-1; i++) { //检查 Lin(i,i+1) 与前面每一条不直接相连的线段
for(int j = 1; j < i; j++) {
if(SegmentProperIntersection(p[i], p[i+1], p[j-1], p[j])) {
return true;
}
}
}
//判断最后一条线段p[0]_p[n-1]
//从第二条线段一直比较到第 n-2 条线段
for(int i = 1; i < n-2 ; i++) { //p[i]__p[i+1]
if(SegmentProperIntersection(p[0],p[n-1],p[i],p[i+1])) {
return true;
}
}
return false;
}
//叉积求面积
double Area() {
double area = 0;
for(int i = 1; i < n-1; i++)
area += Cross(p[i]-p[0], p[i+1]-p[0]);
return fabs(area) / 2.0;
}
int main()
{
int test = 0;
while(scanf("%d", &n) != EOF) {
if(n == 0) break;
double x,y;
for(int i = 0; i < n; i++) {
scanf("%lf%lf", &x,&y);
p[i] = Point(x,y);
}
if(n < 3) { //如果小于三个点, 肯定不能求面积
printf("Figure %d: Impossible\n", ++test);
printf("\n");
continue;
}
if(haveCross()) { //如果有线段相交的情况
printf("Figure %d: Impossible\n", ++test);
printf("\n");
continue;
}
else printf("Figure %d: %.2lf", ++test,Area());
printf("\n");
}
return 0;
}
/**
几组全为 impossible 的数据
*/
/*
7
0 0
4 0
2 1
4 3
3 3
3 2
1 3
7
0 0
1 1
3 0
5 1
5 -1
3 0
1 -1
5
0 0
4 0
3 1
2 0
1 1
*/