UVALive 5075 Intersection of Two Prisms(柱体体积交)
题意:给出两个柱体,一个平行于z轴,设这个截面为A,在XOY面,一个平行于y轴,设这个截面为B,在XOZ面。求两个柱体的公共体积大小。
思路:我们用平行于YOZ的面去切这个公共 体积,因为所有数字为整数,我们可以在x方向每隔1切一次,这样就切成了一些长度为1的窄条,设[i-1,i]的这个窄条在i-1处在z方向的长度为 z[i-1],在y方向的长度为y[i-1],同理i处为z[i]和y[i]。z[i]其实就是B在x=i时上下两个z之差,y[i]就是A在x=i时两 个y之差。如下图:

我们令a=y[i]-y[i-1],b=y[i-1],c=z[i]-z[i-1],d=z[i-1],那么y对x在这个长度为1上的变化方程就是y=ax+b,同理z为z=cx+d,0<=x<=1,那么体积为:
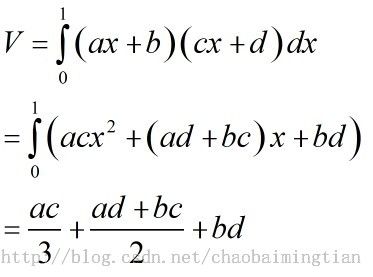
int sgn(double x)
{
if(x>EPS) return 1;
if(x<-EPS) return -1;
return 0;
}
struct POINT
{
int x,y;
POINT(){}
POINT(int _x,int _y)
{
x=_x;
y=_y;
}
void get()
{
RD(x,y);
}
};
struct point
{
double x,y;
point(){}
point(double _x,double _y)
{
x=_x;
y=_y;
}
void get()
{
RD(x); RD(y);
}
point operator+(point a)
{
return point(x+a.x,y+a.y);
}
point operator-(point a)
{
return point(x-a.x,y-a.y);
}
double operator*(point a)
{
return x*a.y-y*a.x;
}
point operator*(double t)
{
return point(x*t,y*t);
}
double operator^(point a)
{
return x*a.x+y*a.y;
}
double len()
{
return sqrt(x*x+y*y);
}
point zhuanShun(double t)
{
return point(x*cos(t)+y*sin(t),y*cos(t)-x*sin(t));
}
point zhuanNi(double t)
{
return point(x*cos(t)-y*sin(t),x*sin(t)+y*cos(t));
}
point adjust(double L)
{
double d=len();
L/=d;
return point(x*L,y*L);
}
void print()
{
printf("%.3lf %.3lf\n",x+EPS,y+EPS);
}
};
double len(point a)
{
return a.len();
}
struct point3
{
double x,y,z;
point3(){}
point3(double _x,double _y,double _z)
{
x=_x;
y=_y;
z=_z;
}
void get()
{
cin>>x>>y>>z;
}
point3 operator+(point3 a)
{
return point3(x+a.x,y+a.y,z+a.z);
}
point3 operator-(point3 a)
{
return point3(x-a.x,y-a.y,z-a.z);
}
point3 operator*(point3 a)
{
return point3(y*a.z-z*a.y,z*a.x-x*a.z,x*a.y-y*a.x);
}
point3 operator*(double t)
{
return point3(x*t,y*t,z*t);
}
double operator^(point3 a)
{
return x*a.x+y*a.y+z*a.z;
}
point3 operator/(double t)
{
return point3(x/t,y/t,z/t);
}
double len()
{
return sqrt(x*x+y*y+z*z);
}
point3 adjust(double L)
{
double t=len();
L/=t;
return point3(x*L,y*L,z*L);
}
void print()
{
printf("%.10lf %.10lf %.10lf\n",x+EPS,y+EPS,z+EPS);
}
};
double len(point3 a)
{
return a.len();
}
double getArea(point3 a,point3 b,point3 c)
{
double x=len((b-a)*(c-a));
return x/2;
}
double getVolume(point3 a,point3 b,point3 c,point3 d)
{
double x=(b-a)*(c-a)^(d-a);
return x/6;
}
point3 pShadowOnPlane(point3 p,point3 a,point3 b,point3 c)
{
point3 v=(b-a)*(c-a);
if(sgn(v^(a-p))<0) v=v*-1;
v=v.adjust(1);
double d=fabs(v^(a-p));
return p+v*d;
}
double lineToLine(point3 a,point3 b,point3 p,point3 q)
{
point3 v=(b-a)*(q-p);
return fabs((a-p)^v)/len(v);
}
int pInPlane(point3 p,point3 a,point3 b,point3 c)
{
double S=getArea(a,b,c);
double S1=getArea(a,b,p);
double S2=getArea(a,c,p);
double S3=getArea(b,c,p);
return sgn(S-S1-S2-S3)==0;
}
int opposite(point3 p,point3 q,point3 a,point3 b,point3 c)
{
point3 v=(b-a)*(c-a);
double x=v^(p-a);
double y=v^(q-a);
return sgn(x*y)<0;
}
int segCrossTri(point3 p,point3 q,point3 a,point3 b,point3 c)
{
return opposite(p,q,a,b,c)&&
opposite(a,b,p,q,c)&&
opposite(a,c,p,q,b)&&
opposite(b,c,p,q,a);
}
double pToPlane(point3 p,point3 a,point3 b,point3 c)
{
double v=((b-a)*(c-a)^(p-a))/6;
double s=len((b-a)*(c-a))/2;
return fabs(3*v/s);
}
double pToLine(point3 p,point3 a,point3 b)
{
double S=len((a-p)*(b-p));
return S/len(a-b);
}
double pToSeg(point3 p,point3 a,point3 b)
{
if(sgn((p-a)^(b-a))<=0) return len(a-p);
if(sgn((p-b)^(a-b))<=0) return len(b-p);
return pToLine(p,a,b);
}
double pToPlane1(point3 p,point3 a,point3 b,point3 c)
{
point3 k=pShadowOnPlane(p,a,b,c);
if(pInPlane(k,a,b,c)) return pToPlane(p,a,b,c);
double x=pToSeg(p,a,b);
double y=pToSeg(p,a,c);
double z=pToSeg(p,b,c);
return min(x,min(y,z));
}
double getAng(point3 a,point3 b)
{
double x=(a^b)/len(a)/len(b);
return acos(x);
}
double segToSeg(point3 a,point3 b,point3 p,point3 q)
{
point3 v=(b-a)*(q-p);
double A,B,A1,B1;
A=((b-a)*v)^(p-a);
B=((b-a)*v)^(q-a);
A1=((p-q)*v)^(a-q);
B1=((p-q)*v)^(b-q);
if(sgn(A*B)<=0&&sgn(A1*B1)<=0)
{
return lineToLine(a,b,p,q);
}
double x=min(pToSeg(a,p,q),pToSeg(b,p,q));
double y=min(pToSeg(p,a,b),pToSeg(q,a,b));
return min(x,y);
}
struct face
{
int a,b,c,ok;
face(){}
face(int _a,int _b,int _c,int _ok)
{
a=_a;
b=_b;
c=_c;
ok=_ok;
}
};
struct _3DCH
{
face F[N<<2];
int b[N][N],cnt,n;
point3 p[N];
int getDir(point3 t,face F)
{
double x=(p[F.b]-p[F.a])*(p[F.c]-p[F.a])^(t-p[F.a]);
return sgn(x);
}
void deal(int i,int x,int y)
{
int f=b[x][y];
if(!F[f].ok) return;
if(getDir(p[i],F[f])==1) DFS(i,f);
else
{
b[y][x]=b[x][i]=b[i][y]=cnt;
F[cnt++]=face(y,x,i,1);
}
}
void DFS(int i,int j)
{
F[j].ok=0;
deal(i,F[j].b,F[j].a);
deal(i,F[j].c,F[j].b);
deal(i,F[j].a,F[j].c);
}
void construct()
{
int i,j,k=0;
for(i=1;i<n;i++) if(sgn(len(p[i]-p[0])))
{
swap(p[i],p[1]);
k++;
break;
}
if(k!=1) return;
for(i=2;i<n;i++) if(sgn(getArea(p[0],p[1],p[i])))
{
swap(p[i],p[2]);
k++;
break;
}
if(k!=2) return;
for(i=3;i<n;i++) if(sgn(getVolume(p[0],p[1],p[2],p[i])))
{
swap(p[i],p[3]);
k++;
break;
}
if(k!=3) return;
cnt=0;
FOR0(i,4)
{
face k=face((i+1)%4,(i+2)%4,(i+3)%4,1);
if(getDir(p[i],k)==1) swap(k.b,k.c);
b[k.a][k.b]=b[k.b][k.c]=b[k.c][k.a]=cnt;
F[cnt++]=k;
}
for(i=4;i<n;i++) FOR0(j,cnt)
{
if(F[j].ok&&getDir(p[i],F[j])==1)
{
DFS(i,j);
break;
}
}
j=0;
FOR0(i,cnt) if(F[i].ok) F[j++]=F[i];
cnt=j;
}
point3 getCenter()
{
point3 ans=point3(0,0,0),o=point3(0,0,0);
double s=0,temp;
int i;
FOR0(i,cnt)
{
face k=F[i];
temp=getVolume(o,p[k.a],p[k.b],p[k.c]);
ans=ans+(o+p[k.a]+p[k.b]+p[k.c])/4*temp;
s+=temp;
}
ans=ans/s;
return ans;
}
double getMinDis(point3 a)
{
double ans=dinf;
int i;
FOR0(i,cnt)
{
face k=F[i];
ans=min(ans,pToPlane(a,p[k.a],p[k.b],p[k.c]));
}
return ans;
}
};
POINT a[N],b[N];
double YMin[N],YMax[N],ZMin[N],ZMax[N];
int n,m;
void init(POINT a[],int n,double Min[],double Max[])
{
a[n+1]=a[1];
int i,j;
POINT p,q;
double k,b;
FOR1(i,n)
{
p=a[i]; q=a[i+1];
if(p.x>q.x) swap(p,q);
Min[p.x]=min(Min[p.x],1.0*p.y);
Max[p.x]=max(Max[p.x],1.0*p.y);
if(p.x==q.x) continue;
k=1.0*(p.y-q.y)/(p.x-q.x);
b=p.y;
for(j=p.x+1;j<=q.x;j++)
{
b+=k;
Min[j]=min(Min[j],b);
Max[j]=max(Max[j],b);
}
}
}
int main()
{
Rush(n)
{
RD(m);
if(!n&&!m) break;
int i;
int xMin1=INF,xMax1=-INF,xMin2=INF,xMax2=-INF;
FOR1(i,n)
{
a[i].get();
a[i].x+=100;
xMin1=min(xMin1,a[i].x);
xMax1=max(xMax1,a[i].x);
}
FOR1(i,m)
{
b[i].get();
b[i].x+=100;
xMin2=min(xMin2,b[i].x);
xMax2=max(xMax2,b[i].x);
}
FOR0(i,N) YMin[i]=ZMin[i]=dinf,YMax[i]=ZMax[i]=-dinf;
init(a,n,YMin,YMax);
init(b,m,ZMin,ZMax);
double y[N],z[N];
int s=max(xMin1,xMin2);
int e=min(xMax1,xMax2);
for(i=s;i<=e;i++)
{
y[i]=YMax[i]-YMin[i];
z[i]=ZMax[i]-ZMin[i];
}
double ans=0,A,B,C,D;
for(i=s+1;i<=e;i++)
{
A=y[i]-y[i-1];
B=y[i-1];
C=z[i]-z[i-1];
D=z[i-1];
ans+=fabs(A*C/3+(A*D+B*C)/2+B*D);
}
PR(ans);
}
}