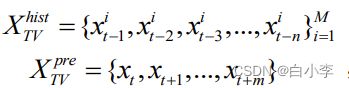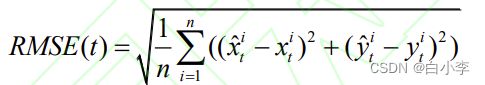2023/5/21周报

目录

摘要

论文阅读

1、标题和现存问题

2、各个结构

3、基于GNN-LSTM-CNN 网络轨迹预测模型

4、实验准备

5、实验结果

深度学习

1、费舍尔判别

2、步骤具体化

3、GCN

总结

---

摘要

本周在论文阅读上，阅读了一篇基于GNN-LSTM-CNN网络的6G车辆轨迹预测算法的论文。文章提出了一种三通道神经网络模型，使用LSTM提取车辆轨迹信息特征， 使用GNN提取不同车辆之间的交互特征，使用CNN提取车道结构特征。模型通过计算三通道特征向量的权重得到目标车辆预测的轨迹，经实验验证模型效果优秀。在深度学习上，对于费舍尔判别进行了学习，同时思考了下未来方向。

This week,in terms of thesis reading,perusaling a paper on a 6G vehicle trajectory prediction algorithm based on GNN-LSTM-CNN network.The article proposes a three channel neural network model.Using LSTM to extract vehicle trajectory information features, GNN to extract interaction features between different vehicles, and CNN to extract lane structure features.The model obtains the predicted trajectory of the target vehicle by calculating the weight of the three channel feature vectors.The model has been experimentally verified to have excellent performance.In deep learning, studying about Fisher's discriminant analysis and considering future directions

论文阅读

1、标题和现存问题

标题：基于GNN-LSTM-CNN网络的6G车辆轨迹预测算法

现存问题：轨迹预测的方法，主要分为三大类。分为基于物理模型的轨迹预测方法，基 于模式的轨迹预测方法，以及基于交互感知的轨迹预测方法。基于物理模型的预测方法没有考虑道路障碍物以及道路 车辆的影响，无法在道路拥挤的情况下准确预测目标车辆的轨迹。基于模式的方法忽略了道路环境以及道路车辆的影响。基于交互感知的方法感知周围车辆状态以及道路环境等因素后，根据道路车辆之间的互相影响以及道路环境对于车辆的约束来预测车辆的轨迹。

文章提出的解决方法：设计GNN-LSTM-CNN网络结构， 能够同时提取车辆之间交互状态信息、车道线信息以及目标车辆的轨迹信息做联合预测。通过图神经网络 提取车辆之间的交互关系，通过卷积神经网络来提取车道线信息，通过长短时记忆网络提取目标车辆轨迹 信息，根据权重预测目标车辆的轨迹。

2、各个结构

预测未来一段时间内车辆的轨迹：

 

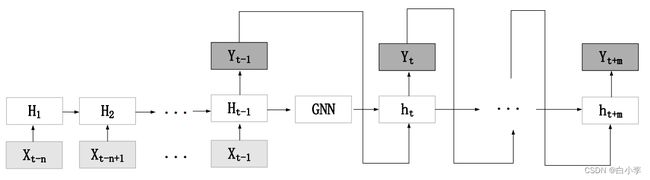
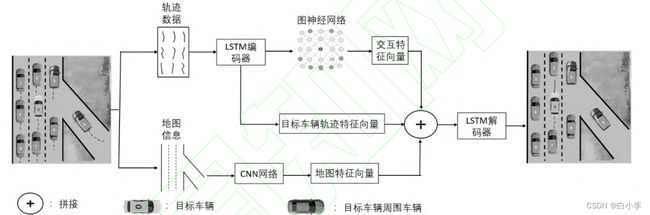
本文采用编码器-解码器架构来处理目标车辆的轨迹序列生成问题。通过 LSTM 编码器对目标车辆以 及相关车辆的轨迹序列进行编码，通过图神经网络对车辆之间的交互关系进行编码，将两者编码的结果剪 切之后共同输入到LSTM 解码器中解析出目标车辆未来一段时间的轨迹。

LSTM 编解码器结构

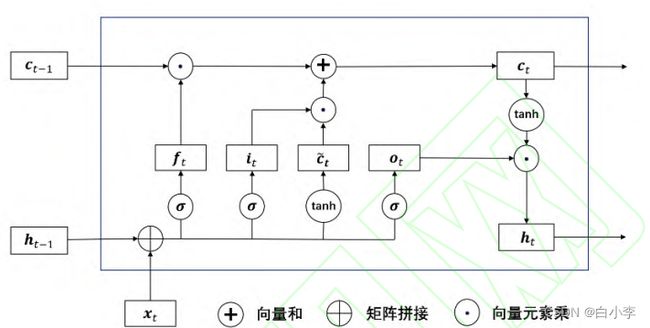
长短期记忆神经网络是循环神经网络的一种结构，通过引入记忆门的方式来减小梯度消失问题，通过记忆门来实现各记忆细 胞信息的传递，有效的解决了时间序列预测中的长期依赖问题，长短期记忆网络结构有输出门，遗忘门以 及更新门三种。

 

车辆的历史轨迹与车辆的行驶特征密切相关，采用LSTM 编码器对车辆的历史轨迹进行特征提取，提 取出的特征向量，建立换道前后轨迹的联系，更加深入的分析车辆换道前的特征，生成轨迹序列。LSTM 编码器如下图所示:

 

有人驾驶车辆在换道决策执行时，会观察周围的道路情况与车辆情况，根据自身意图来进行换道决策。 有学者通过目标车辆的历史轨迹可以来预测车辆是否换道，但是预测的精度不足[20]。本文通过图神经网络 来提取目标车辆周围的车辆对目标车辆的影响，通过长短时记忆网络来提取目标车辆自身轨迹的特征，通 过环境特征向量来提取车道结构对轨迹的影响，最终将提取出的特征向量拼接作为轨迹预测的特征向量。

图神经网络

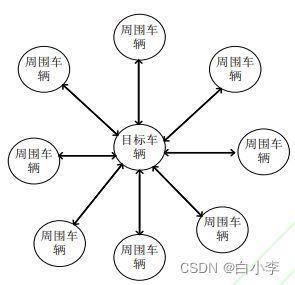
图神经网络（Graph Neural Network，GNN）是一种分布模型，通过图节点之间的消息交换来表示节点之 间的交互关系，其基于图域数据的特征提取和表示优势，可以更好的挖掘各个节点之间内在关联。交互影响模型如下图所示：

 

道路上的车辆的运动轨迹会受到其它交通参与者的影响。同一个时空下的车辆之间互相之间会影响彼 此的轨迹。如目标车辆左边车辆有车辆经过时，目标车辆无法向左变道。目标车辆可能会跟随前方车辆行 驶，或者左方车辆向目标车辆变道时目标车辆会减速。本文对高速公路场景下车辆的轨迹做特征提取，通 过计算目标车辆与周围车辆的相对速度、偏航角、加速度的差值来表征周围车辆与目标车辆的关系，作为 图结构中的边，同时将目标车辆与周围车辆轨迹的特征向量作为图结构的节点，来构建图神经网络的基本 结构。

卷积神经网络

文章设计了一个卷积神经网络，通过引入门限机制，从道路的俯视图 照片中提取道路特征，并且根据目标车辆当前的位置，选择该位置为中心的道路特征向量作为车辆轨迹预 测精度的影响因子之一。门限机制的作用在于目标车辆的轨迹大部分情况下受到周围车辆的影响占比比较 大，当目标车辆与目标车辆周围车辆交互特征向量的影响因子较大时，此时目标大概率是在道路中央，目 标车辆的形式轨迹与地图特征无关，因此该条件下停止对于地图特征向量的提取。

根据目标车辆在地图中的状态来选择对应的地图特征：

 

那么目标车辆i 在t 时刻是否受到地图 信息的影响可以表示为：

 

3、基于GNN-LSTM-CNN 网络轨迹预测模型

模型采用三通道数据处理方法来预测目标车辆的轨迹。分别是使用 GNN 通道提取车辆间交互信息、使 用 LSTM 通道提取目标车辆轨迹信息以及使用 CNN 通道提取车道结构特征。车辆间交互信息指的是同一 时空下车辆之间互相影响，如目标车辆的左前方车辆打出右转指示灯并且向右变道，目标车辆就会减速或 者向其它车辆变道或者当目标车辆后方有车辆超车时，目标车辆大概率减速等等。

 

本模型的输入相比于其它模型增加了地图模块，为：

在模型中，文章采用了有向图来表示车辆之间的交互作用，并且使用注意力机制来提取车辆之间 的交互特征。通过引入门限机制，来有选择性的引入地图信息。通过注意力机制来得到最终的LSTM 解码 器的输入特征，使用LSTM 解码器预测目标车辆的轨迹序列。

4、实验准备

数据集：NGSIM中的车辆轨迹数据

预处理过程中，为了保证数据的稳定性以及可靠性，文章只选取在中间五条车道的车辆轨迹数据， 且只选取发生变道的车辆的轨迹数据。且发生变道的时刻记录的帧数在第300 帧与第1900 帧之间。同时为 了保证确定变道，变道过程前后距离需要大于三米。经过以上预处理之后，筛选出总共370 个目标车辆的轨迹。

预测轨迹数据的解码器使用含 有64维隐藏状态的长短时记忆网络实现，交互编码器使用图注意力网络[31]来实现，使用三头注意力机制 来稳定训练过程。该模型经过140个epoch的训练，以最小化均方根误差的方式，使用Adam优化器，学习率为0.001。采用Multiprocessing对多个模型进行多核并行运算，以保证最短的程序运行时间。

文使用预测的轨迹序列与真实的轨迹序列之间的均方根误差（RMSE）来评估不同的模型，计算未来5秒内每个预测时间步的均方根误差。评估方式公式如下：

 

5、实验结果

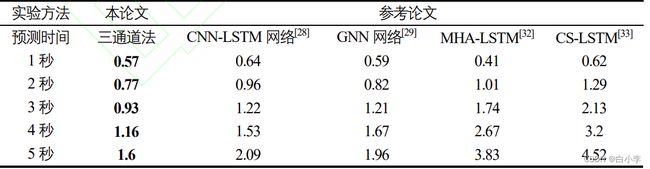
对比模型：CNN-LSTM、GNN、MHA-LSTM[、CS-LSTM

 

相比于CNN-LSTM网络，轨迹预测在1s、2s、3s、4s、5s的预测轨 迹的均方误差分别提升10.9%、19.7%、31.2%、30.5、18.3%，可以说明图神经网络对于目标车辆与周围车 辆关系特征的提取优于卷积神经网络。对比单独只有 GNN的网络，预测的轨迹的均方误差分别提升3.3%、6.0%、9.7%、8.6%、13.9%。对比没有车道线信息的网络结构，本预测的轨迹的均方误差在5s时提升58%。

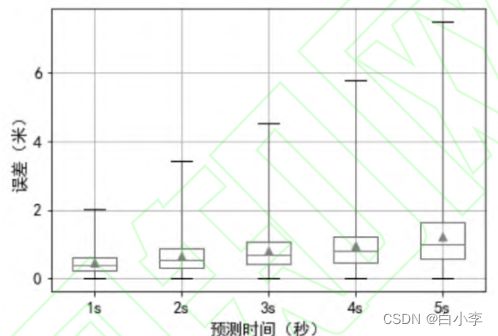
如下图，本文使用箱线图表示本模型的测试数据。从图中可以看出，本模型的测试误差主要集中 在箱体内，4s 时的绝大部分误差 1.5 米之内，每一个时刻误差的箱线图箱体比较集中，代表本模型预测的结果误差比较集中。

 

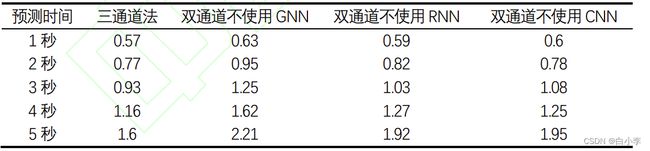
下表为三通道模型的消融实验的结果。通过删除三通道轨迹预测模型中的某一通道模块，观测其轨迹 预测精度效果。从表中可以看出，交互信息对于目标车辆的轨迹影响因素最大，不利用交互信息后轨迹预 测的误差增大最明显，说明交互信息对于轨迹预测精度影响较大。不利用车辆轨迹信息或车道线信息，均 方误差均有上升，说明本模型三种信息均对最终轨迹预测精度有一定作用。

 

不同模型复杂度分析：

 

文章所提出的模型参数数量与训练时间都有部分增加，因为使用的模型增加， 模型分析的数据量变大，使用三通道网络模型来增加轨迹预测的精度。总的来说，模型的计算成本开销有 部分增加，本模型提高了对车辆的计算能力的要求。

深度学习

1、费舍尔判别

费舍尔判别（Fisher's discriminant analysis），也称为线性判别分析（Linear Discriminant Analysis，LDA），是一种经典的模式识别和分类方法。

费舍尔判别旨在通过寻找投影变换，将数据从高维空间映射到低维空间，以实现数据的分类和降维。其核心思想是最大化类别间的差异性，同时最小化类别内的差异性。

具体来说，费舍尔判别分析的步骤如下：

1. 数据准备：收集带有类别标签的训练数据集，其中每个样本都有一组特征向量和对应的类别标签。

2. 计算类别均值向量：对于每个类别，计算其样本的均值向量，表示该类别在特征空间中的中心位置。

3. 计算类别内散布矩阵：计算每个类别内的散布矩阵，用于度量类别内样本的离散程度。

4. 计算类别间散布矩阵：计算类别之间的散布矩阵，用于度量不同类别之间的分离程度。

5. 计算投影向量：通过求解广义特征值问题，计算投影向量，将高维数据映射到一维或更低维的空间。

6. 判别阈值：根据投影后的数据，选择一个阈值将数据划分为不同的类别。

优点：

1. 降维和分类一体化：费舍尔判别能够同时进行降维和分类，将高维数据映射到低维空间，并在映射后的空间中进行分类，从而减少了计算复杂度和存储空间。

2. 最大化类别间差异：费舍尔判别通过最大化类别间的散布矩阵来增加类别之间的差异性，使得不同类别在映射空间中的分离度最大化，有助于提高分类性能。

3. 数据可解释性：费舍尔判别所得到的投影向量具有较好的可解释性，可以解释为在低维空间中最能区分不同类别的方向或特征。

4. 对噪声数据具有鲁棒性：费舍尔判别对数据中的噪声相对鲁棒，因为它考虑了整个类别的统计特性，而不仅仅是单个数据点。

缺点：

1. 线性假设：费舍尔判别是基于线性假设的方法，适用于数据具有线性可分性的情况。当数据不满足线性分布假设时，费舍尔判别的性能可能下降。

2. 类别均衡性：费舍尔判别对类别的分布和样本数目敏感，如果不同类别的样本数量差异较大，可能导致分类结果的偏倚。

3. 特征独立性：费舍尔判别假设特征之间是相互独立的，这在实际应用中并不总是成立。如果特征之间存在相关性或依赖关系，费舍尔判别的效果可能受到影响。

4. 高维数据处理：当输入数据维度非常高时，费舍尔判别可能面临维度灾难和计算复杂度增加的问题。因此，在高维数据的情况下，需要采取降维等方法来改善费舍尔判别的性能。

2、步骤具体化

1. 计算每个类别的均值向量，表示在原始特征空间中每个类别的平均值。

2. 计算类别内散布矩阵，度量类别内数据的变化程度。它通过计算每个类别内数据点与该类别均值之间的差异来得到。

3. 计算类别间散布矩阵，度量类别之间的差异程度。它通过计算每个类别均值与整体均值之间的差异，并根据类别样本数量进行加权求和得到。

4. 解决广义特征值问题，即计算类别内散布矩阵的逆矩阵乘以类别间散布矩阵的特征向量。

5. 对特征向量进行排序，按照对应的特征值从大到小进行排序。

6. 选择第一个特征向量作为投影向量，因为它对应的特征值是最大的，表示它包含了最大的类别间差异。

7. 返回计算得到的投影向量和类别均值向量。

通过在低维空间中找到最佳的投影方向，它能够最大程度地区分不同类别的数据。

import numpy as np
​
def fisher_discriminant_analysis(X, y):
    # 计算类别均值向量
    class_means = []
    for label in np.unique(y):
        class_means.append(np.mean(X[y == label], axis=0))
    class_means = np.array(class_means)
​
    # 计算类别内散布矩阵
    within_class_scatter = np.zeros((X.shape[1], X.shape[1]))
    for label in np.unique(y):
        class_samples = X[y == label]
        class_mean = class_means[label]
        class_scatter = (class_samples - class_mean).T.dot(class_samples - class_mean)
        within_class_scatter += class_scatter
​
    # 计算类别间散布矩阵
    overall_mean = np.mean(X, axis=0)
    between_class_scatter = np.zeros((X.shape[1], X.shape[1]))
    for label in np.unique(y):
        class_mean = class_means[label]
        between_class_scatter += len(X[y == label]) * (class_mean - overall_mean).reshape(-1, 1) @ (class_mean - overall_mean).reshape(1, -1)
​
    # 计算广义特征值问题的解
    eigenvalues, eigenvectors = np.linalg.eig(np.linalg.inv(within_class_scatter) @ between_class_scatter)
​
    # 对特征向量进行排序
    sorted_indices = np.argsort(eigenvalues)[::-1]
    eigenvalues = eigenvalues[sorted_indices]
    eigenvectors = eigenvectors[:, sorted_indices]
​
    # 选择投影向量
    projection_vector = eigenvectors[:, 0]
​
    # 返回投影向量和类别均值向量
    return projection_vector, class_means
​
# 示例数据
X = np.array([[5.1, 3.5, 1.4, 0.2],
              [4.9, 3.0, 1.4, 0.2],
              [5.7, 2.8, 4.1, 1.3],
              [6.3, 3.3, 6.0, 2.5],
              [7.6, 3.0, 6.6, 2.1]])
y = np.array([0, 0, 1, 2, 2])
​
# 应用费舍尔判别
projection_vector, class_means = fisher_discriminant_analysis(X, y)
​
# 输出投影向量和类别均值向量
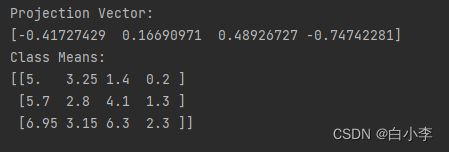
print("Projection Vector:")
print(projection_vector)
print("Class Means:")
print(class_means)
​

 

3、GCN

对于GCN部分，对于数据先进行整理，将每一个站点作为一个节点，每个站点内的数据作为节点的属性，将站点之间按实际道路连接起来，构成一张图，边上具有权重。权重设定进行随机初始化，由神经网络训练出来。在GCN的目的就是将其站点的联系给找出来，通过神经网络挖掘其内在的规律，并将其设定为参数的样子，传递给时序模型部分，在预测接下来的大气情况中，有更多重要的因素参与进来，提升模型的说服力。

总结

本周主要是处理课程上的事，对于学习方向学得比较少，这周结束，课程也基本结束了，接下来就可以把重心放在研究方向了，对于研究方向还是挺迷茫，一下想不到创新点，原因应该是相关论文看得比较少，下周开始计划先找一篇最新的综述来看，先做到彻底了解。