第十四届蓝桥杯大赛软件赛省赛(C/C++ 大学C组)
蓝桥杯 2023年省赛真题
C/C++ 大学C组
- 试题 A: 求和
- 试题 B: 工作时长
- 试题 C: 三国游
- 试题 D: 填充
- 试题 E: 翻转
- 试题 F: 子矩阵
- 试题 G: 互质数的个数
- 试题 H: 异或和之差
- 试题 I: 公因数匹配
- 试题 J: 子树的大小
试题 A: 求和
本题总分: 5 5 5 分
【问题描述】
求 1 1 1 (含)至 20230408 20230408 20230408 (含)中每个数的和。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
204634714038436
自然数列求和, 1 + 2 + ⋯ + n = n ( n + 1 ) 2 1+2+\cdots+n=\cfrac {n(n+1)}2 1+2+⋯+n=2n(n+1)。
#include 或者迭代答案。
#include 试题 B: 工作时长
本题总分: 5 5 5 分
【问题描述】
小蓝手里有一份 2022 年度自己的上班打卡记录文件,文件包含若干条打卡记录,每条记录的格式均为 “ y y y y \rm yyyy yyyy- M M \rm MM MM- d d H H : m m : s s \rm dd\ HH:mm:ss dd HH:mm:ss”,即按照年 -月 -日时:分: 秒的形式记录着一个时间点 (采用 24 24 24 小时进制)。由于某些原因,这份文件中的时间记录并不是按照打卡的时间顺序记录的,而是被打乱了。但我们保证小蓝每次上班和下班时都会正常打卡,而且正好打卡一次,其它时候不会打卡。每一对相邻的上 -下班打卡之间的时间就是小蓝本次的工作时长,例如文件内容如下的话:
2022 2022 2022- 01 01 01- 01 12 : 00 : 05 01\ 12:00:05 01 12:00:05
2022 2022 2022- 01 01 01- 02 00 : 20 : 05 02\ 00:20:05 02 00:20:05
2022 2022 2022- 01 01 01- 01 07 : 58 : 02 01\ 07:58:02 01 07:58:02
2022 2022 2022- 01 01 01- 01 16 : 01 : 35 01\ 16:01:35 01 16:01:35
表示文件中共包含了两段上下班记录, 1 ) 2022 1)2022 1)2022- 01 01 01- 01 07 : 58 : 02 ∼ 2022 01\ 07:58:02 ∼ 2022 01 07:58:02∼2022- 01 01 01- 01 12 : 00 : 05 01\ 12:00:05 01 12:00:05,工作时长为 14523 14523 14523 秒; 2 ) 2022 2)2022 2)2022- 01 01 01- 01 16 : 01 : 35 ∼ 2022 01\ 16:01:35 ∼ 2022 01 16:01:35∼2022- 01 01 01- 02 00 : 20 : 05 02\ 00:20:05 02 00:20:05 工作时长为 29910 29910 29910 秒;工作时长一共是 14523 + 29910 = 44433 14523+29910=44433 14523+29910=44433 秒。现在小蓝想知道在 2022 2022 2022 年度自己的工作时长一共是多少秒?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
unknow
没数据,写个差不多的程序意思一下。
#include 试题 C: 三国游
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 10 10 10 分
【问题描述】
小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X , Y , Z X, Y, Z X,Y,Z (一开始可以认为都为 0 0 0 )。游戏有 n n n 个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i i i 个事件发生时会分别让 X , Y , Z X, Y, Z X,Y,Z 增加 A i , B i , C i A_i, B_i,C_i Ai,Bi,Ci。
当游戏结束时 (所有事件的发生与否已经确定),如果 X , Y , Z X, Y, Z X,Y,Z 的其中一个大于另外两个之和,我们认为其获胜。例如,当 X > Y + Z X > Y + Z X>Y+Z 时,我们认为魏国获胜。小蓝想知道游戏结束时如果有其中一个国家获胜,最多发生了多少个事件?
如果不存在任何能让某国获胜的情况,请输出 − 1 −1 −1。
【输入格式】
输入的第一行包含一个整数 n n n。
第二行包含 n n n 个整数表示 A i A_i Ai,相邻整数之间使用一个空格分隔。
第三行包含 n n n 个整数表示 B i B_i Bi,相邻整数之间使用一个空格分隔。
第四行包含 n n n 个整数表示 C i C_i Ci,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
3
1 2 2
2 3 2
1 0 7
【样例输出】
2
【样例说明】
发生两个事件时,有两种不同的情况会出现获胜方。
发生 1 , 2 1, 2 1,2 事件时蜀国获胜。
发生 1 , 3 1, 3 1,3 事件时吴国获胜。
【评测用例规模与约定】
对于 40 % 40\% 40% 的评测用例, n ≤ 500 n ≤ 500 n≤500;
对于 70 % 70\% 70% 的评测用例, n ≤ 5000 n ≤ 5000 n≤5000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 1 ≤ A i , B i , C i ≤ 1 0 9 1 ≤ n ≤ 10^5,1 ≤ A_i, B_i,C_i ≤ 10^9 1≤n≤105,1≤Ai,Bi,Ci≤109。
贪心
同时考虑三个国家是相当困难的,于是考虑分别求出魏蜀吴分别获胜的话最大事件数,最优答案就是这若干个数中的最大值。
以魏举例,记第 i i i 个事件对魏获胜的贡献为 x i − y i − z i x_i -y_i -z_i xi−yi−zi,按贡献降序重排事件,找到一个 k k k,满足 ∑ i = 1 k x i > ∑ i = 1 k ( y i + z i ) \sum_{i=1}^kx_i >\sum_{i=1}^k(y_i + z_i) ∑i=1kxi>∑i=1k(yi+zi) 且 k k k 尽可能大,若 k < n k < n k<n,易知 ∑ i = 1 k + 1 x i ≤ ∑ i = 1 k + 1 ( y i + z i ) \sum_{i=1}^{k+1}x_i \leq\sum_{i=1}^{k+1}(y_i + z_i) ∑i=1k+1xi≤∑i=1k+1(yi+zi) 且 [ 1 , k ] [1,k] [1,k] 间的或 ( k , n ] (k,n] (k,n] 间的事件交换不会对和式值造成影响, [ 1 , k ] [1,k] [1,k] 间与 ( k , n ] (k,n] (k,n] 间的元素交换会使 ∑ i = 1 k + 1 ( x i − y i − z i ) \sum_{i=1}^{k+1}(x_i-y_i - z_i) ∑i=1k+1(xi−yi−zi) 变小,不等式无法成立,从而 k 对魏来说最优。
#include 22岁,喜欢屎山代码。
试题 D: 填充
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 10 10 10 分
【问题描述】
有一个长度为 n n n 的 01 01 01 串,其中有一些位置标记为 ? ? ?,这些位置上可以任意填充 0 0 0 或者 1 1 1,请问如何填充这些位置使得这个 01 01 01 串中出现互不重叠的 00 00 00 和 11 11 11 子串最多,输出子串个数。
【输入格式】
输入一行包含一个字符串。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
1110?0
【样例输出】
2
【样例说明】
如果在问号处填 0 0 0,则最多出现一个 00 00 00 和一个 11 : 111000 11:111000 11:111000。
【评测用例规模与约定】
对于所有评测用例, 1 ≤ n ≤ 1000000 1 ≤ n ≤ 1000000 1≤n≤1000000。
贪心
如果以01相接的地方为断点,将01串拆分开来,如1110?0拆分成111、0?0,则显然第二段中的问号应填0,于是只需考虑若干问号存在01之间的情况,如果若干问号的左侧段长为奇数,则考虑将一个问号变为左侧段对应的值,使总答案加一,然后将所有问号变为右侧段对应的值,若剩余问号为奇数则这个数字除二向下取整是雷打不动的,而多余的一个变为左侧对答案无贡献,所以直接变右,这么模拟着递推过来就行。
实现时连续的问号同时当做0、1来看待,然后找到子串后清空累计即可。
#include 好像又把代码写成一坨了
试题 E: 翻转
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 15 15 15 分
【问题描述】
小蓝用黑白棋的 n n n 个棋子排成了一行,他在脑海里想象出了一个长度为 n n n 的 01 01 01 串 T T T,他发现如果把黑棋当做 1 1 1,白棋当做 0 0 0,这一行棋子也是一个长度为 n n n 的 01 01 01 串 S S S。
小蓝决定,如果在 S S S 中发现一个棋子和它两边的棋子都不一样,就可以将其翻转变成另一个颜色。也就是说,如果 S S S 中存在子串 101 101 101 或者 010 010 010,就可以选择将其分别变为 111 111 111 和 000 000 000,这样的操作可以无限重复。
小蓝想知道最少翻转多少次可以把 S S S 变成和 T T T 一模一样。
【输入格式】
输入包含多组数据。
输入的第一行包含一个正整数 D D D 表示数据组数。
后面 2 D 2D 2D 行每行包含一个 01 01 01 串,每两行为一组数据,第 2 i − 1 2i − 1 2i−1 行为第 i i i 组数据的 T i T_i Ti,第 2 i 2i 2i 行为第 i i i 组数据的 S i S_i Si, S i S_i Si 和 T i T_i Ti 长度均为 n i n_i ni。
【输出格式】
对于每组数据,输出一行包含一个整数,表示答案,如果答案不存在请输出 −1。
【样例输入】
2
1000111
1010101
01000
11000
【样例输出】
2
-1
【评测用例规模与约定】
对于 20 % 20\% 20% 的评测用例, 1 ≤ ∑ 1 D n i ≤ 10 1 ≤\sum_1^{{}_D} n_i ≤ 10 1≤∑1Dni≤10;
对于所有评测用例,保证 1 ≤ ∑ 1 D n i ≤ 1 0 6 , n i > 0 1 ≤\sum_1^{{}_D} n_i ≤ 10^6 ,n_i > 0 1≤∑1Dni≤106,ni>0。
由题意可知,端点棋子是无法翻转的,而当某一个棋子翻转时,它与相邻棋子连续相同,故无法产生新的翻转点,因此端点特判然后遍历模拟就行。
#include 试题 F: 子矩阵
时间限制: 2.0 s 2.0\mathrm s 2.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 15 15 15 分
【问题描述】
给定一个 n × m n × m n×m ( n n n 行 m m m 列)的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b a × b a×b ( a a a 行 b b b 列)的子矩阵的价值的和。
答案可能很大,你只需要输出答案对 998244353 998244353 998244353 取模后的结果。
【输入格式】
输入的第一行包含四个整数分别表示 n , m , a , b n, m, a, b n,m,a,b,相邻整数之间使用一个空格分隔。
接下来 n n n 行每行包含 m m m 个整数,相邻整数之间使用一个空格分隔,表示矩阵中的每个数 A i , j A_{i, j} Ai,j。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
2 3 1 2
1 2 3
4 5 6
【样例输出】
58
【样例说明】
1 × 2 + 2 × 3 + 4 × 5 + 5 × 6 = 58 1 × 2 + 2 × 3 + 4 × 5 + 5 × 6 = 58 1×2+2×3+4×5+5×6=58。
【评测用例规模与约定】
对于 40 % 40\% 40% 的评测用例, 1 ≤ n , m ≤ 100 1 ≤ n, m ≤ 100 1≤n,m≤100;
对于 70 % 70\% 70% 的评测用例, 1 ≤ n , m ≤ 500 1 ≤ n, m ≤ 500 1≤n,m≤500;
对于所有评测用例, 1 ≤ a ≤ n ≤ 1000 1 ≤ b ≤ m ≤ 1000 1 ≤ A i , j ≤ 1 0 9 1 ≤ a ≤ n ≤ 1000\ 1 ≤ b ≤ m ≤ 1000\ 1 ≤ A_{i, j} ≤ 10^9 1≤a≤n≤1000 1≤b≤m≤1000 1≤Ai,j≤109。
通过单调队列,先将矩阵(i-a+1,j)(i,j)的最值求出,然后如法炮制求出(i-a+1,j-b+1)(i,j-b+1)、(i-a+1,j-b+2)(i,j-b+2)、…、(i-a+1,j)(i,j)的最值,即(i-a+1,j-b+1)(i,j)的最值。
单调队列求最值懒得讲了,关键字:单调队列、滑动窗口、区间最值,自己搜着看吧。
#include 省了个保存原数组的空间开销,代码一坨
试题 G: 互质数的个数
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 20 20 20 分
【问题描述】
给定 a , b a, b a,b,求 1 ≤ x < a b 1 ≤ x < a^b 1≤x<ab 中有多少个 x x x 与 a b a^b ab 互质。由于答案可能很大,你只需要输出答案对 998244353 998244353 998244353 取模的结果。
【输入格式】
输入一行包含两个整数分别表示 a , b a, b a,b,用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入 1】
2 5
【样例输出 1】
16
【样例输入 2】
12 7
【样例输出 2】
11943936
【评测用例规模与约定】
对于 30 % 30\% 30% 的评测用例, a , b ≤ 1 0 6 a,b ≤ 10^6 a,b≤106;
对于 70 % 70\% 70% 的评测用例, a ≤ 1 0 6 , b ≤ 1 0 9 a ≤ 10^6,b ≤ 10^9 a≤106,b≤109;
对于所有评测用例, 1 ≤ a ≤ 1 0 9 , 1 ≤ b ≤ 1 0 18 1 ≤ a ≤ 10^9,1 ≤ b ≤ 10^{18} 1≤a≤109,1≤b≤1018。
题意就是求欧拉函数 φ ( a b ) \varphi(a^b) φ(ab),由算术基本定理可知 n = p 1 a 1 p 2 a 2 ⋯ p s a s n=p_1^{a_1}p_2^{a_2}\cdots p_s^{a_s} n=p1a1p2a2⋯psas, φ ( n ) = ∏ i = 1 s φ ( p i a i ) = ∏ i = 1 s p i a i − 1 ( p i − 1 ) = ∏ i = 1 s p i a i ( 1 − 1 p i ) = p 1 a 1 p 2 a 2 ⋯ p s a s ∏ i = 1 s ( 1 − 1 p i ) = n ∏ i = 1 s ( 1 − 1 p i ) \begin{split} \varphi(n) &=\prod_{i=1}^s\varphi(p_i^{a_i})\\ &=\prod_{i=1}^sp_i^{a_i-1}(p_i-1)\\ &=\prod_{i=1}^sp_i^{a_i}(1-\frac 1{p_i})\\ &=p_1^{a_1}p_2^{a_2}\cdots p_s^{a_s}\prod_{i=1}^s(1-\frac 1{p_i})\\ &=n\prod_{i=1}^s(1-\frac 1{p_i}) \end{split} φ(n)=i=1∏sφ(piai)=i=1∏spiai−1(pi−1)=i=1∏spiai(1−pi1)=p1a1p2a2⋯psasi=1∏s(1−pi1)=ni=1∏s(1−pi1)而对于 a a a与 a b a^b ab,显然它们的 ∏ i = 1 s ( 1 − 1 p i ) \prod_{i=1}^s(1-\frac 1{p_i}) ∏i=1s(1−pi1)部分相等,即本质不同质因数没有变化,故答案为 a b − 1 φ ( a ) a^{b-1}\varphi(a) ab−1φ(a)。
#include 截止2023年5月12日16:31:11,dotcpp上的民间数据有误,当 a a a取 a b a^b ab余数部分,并且 a n s ∤ p ans\not|\ p ans∣ p时才能通过所有用例,错的离谱,害得我de半天bug。
试题 H: 异或和之差
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 20 20 20 分
【问题描述】
给定一个含有 n n n 个元素的数组 A i A_i Ai,你可以选择两个不相交的子段。求出这两个子段内的数的异或和的差值的最大值。
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数 A i A_i Ai,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
6
1 2 4 9 2 7
【样例输出】
14
【样例说明】
两个子段可以分别选 1 1 1 和 4 , 9 , 2 4,9,2 4,9,2,差值为 15 − 1 = 14 15 − 1 = 14 15−1=14。
【评测用例规模与约定】
对于 40 % 40\% 40% 的评测用例, n ≤ 5000 n ≤ 5000 n≤5000;
对于所有评测用例, 2 ≤ n ≤ 2 × 1 0 5 , 0 ≤ A i ≤ 2 20 2 ≤ n ≤ 2 × 10^5,0 ≤ A_i ≤ 2^{20} 2≤n≤2×105,0≤Ai≤220。
01字典树,里面存前缀异或和,然后查询[1,i][i,n]的最值,做个dp最后枚举答案。
#include 试题 I: 公因数匹配
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 25 25 25 分
【问题描述】
给定 n n n 个正整数 A i A_i Ai,请找出两个数 i , j i, j i,j 使得 i < j i < j i<j 且 A i A_i Ai 和 A j A_j Aj 存在大于 1 1 1 的公因数。
如果存在多组 i , j i, j i,j,请输出 i i i 最小的那组。如果仍然存在多组 i , j i, j i,j,请输出 i i i 最小的所有方案中 j j j 最小的那组。
【输入格式】
输入的第一行包含一个整数 n n n。
第二行包含 n n n 个整数分别表示 A 1 A 2 ⋯ A n A_1 A_2 \cdots A_n A1A2⋯An,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含两个整数分别表示题目要求的 i , j i, j i,j,用一个空格分隔。
【样例输入】
5
5 3 2 6 9
【样例输出】
2 4
【评测用例规模与约定】
对于 40 % 40\% 40% 的评测用例, n ≤ 5000 n ≤ 5000 n≤5000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 1 ≤ A i ≤ 1 0 6 1 ≤ n ≤ 10^5,1 ≤ A_i ≤ 10^6 1≤n≤105,1≤Ai≤106。
欧拉筛计算出A范围内每个整数的本质不同质因数,易知 1 0 6 10^6 106内整数本质不同质因数不会超过十个,从后往前遍历并记录每个因数最新一次出现位置,线性时间就能跑出来。
#include 试题 J: 子树的大小
时间限制: 2.0 s 2.0\mathrm s 2.0s 内存限制: 256.0 M B 256.0\mathrm{MB} 256.0MB 本题总分: 25 25 25 分
【问题描述】
给定一棵包含 n n n 个结点的完全 m m m 叉树,结点按从根到叶、从左到右的顺序依次编号。
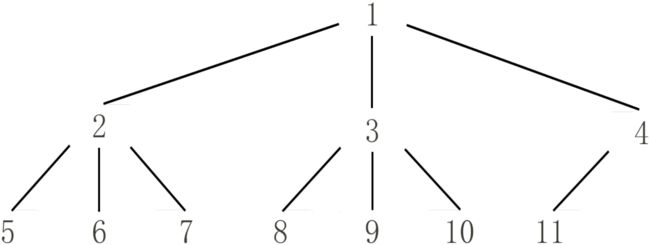
例如下图是一个拥有 11 11 11 个结点的完全 3 3 3 叉树。
你需要求出第 k k k 个结点对应的子树拥有的结点数量。
【输入格式】
输入包含多组询问。
输入的第一行包含一个整数 T T T ,表示询问次数。
接下来 T T T 行,每行包含三个整数 n , m , k n, m, k n,m,k 表示一组询问。
【输出格式】
输出 T T T 行,每行包含一个整数表示对应询问的答案。
【样例输入】
3
1 2 1
11 3 4
74 5 3
【样例输出】
1
2
24
【评测用例规模与约定】
对于 40 % 40\% 40% 的评测用例, T ≤ 50 , n ≤ 1 0 6 , m ≤ 16 T ≤ 50,n ≤ 10^6,m ≤ 16 T≤50,n≤106,m≤16;
对于所有评测用例, 1 ≤ T ≤ 1 0 5 , 1 ≤ k ≤ n ≤ 1 0 9 , 2 ≤ m ≤ 1 0 9 1 ≤ T ≤ 10^5,1 ≤ k ≤ n ≤ 10^9,2 ≤ m ≤ 10^9 1≤T≤105,1≤k≤n≤109,2≤m≤109。
容易发现,高度同为 h h h的节点编号连续,从 1 + ∑ i = 0 h − 1 m i 1+\sum_{i=0}^{h-1}m^i 1+∑i=0h−1mi排到 ∑ i = 0 h m i \sum_{i=0}^hm^i ∑i=0hmi,因此我们可以枚举每一层的编号然后统计是 k k k的子节点的节点的个数,每次询问复杂度为 O ( log m n ) O(\log_mn) O(logmn)。
对于那一段节点是 k k k的子节点,我们记 k k k所在的高度为 h h h, k k k在兄弟节点中的排位为 r r r,则 k + 1 k+1 k+1层是 k k k子节点的节点的序号应落入 [ 1 + ∑ i = 0 h m i + ( r − 1 ) m 1 , 1 + ∑ i = 0 h m i + r m 1 ) [1+\sum_{i=0}^{h}m^i+(r-1)m^1,1+\sum_{i=0}^{h}m^i+rm^1) [1+∑i=0hmi+(r−1)m1,1+∑i=0hmi+rm1)这个区间,对于 h + j h+j h+j层容易找到关系式 [ 1 + ∑ i = 0 h + j − 1 m i + ( r − 1 ) m j , 1 + ∑ i = 0 h m i + r m j ) [1+\sum_{i=0}^{h+j-1}m^i+(r-1)m^j,1+\sum_{i=0}^{h}m^i+rm^j) [1+∑i=0h+j−1mi+(r−1)mj,1+∑i=0hmi+rmj),把模拟题藏成这样,欺负我专科兄弟是吧。
#include 也可以简化一点,将答案拆成最后一层和其余两部分,这样答案就是一个满 m m m叉树节点个数加上上述方法求出的最后一层节点个数,这么写代码可能会显得更可读,大概。