数字信号处理7
昨天着重就是离散时间系统的复习，包括离散时间系统的分类有哪些，是根据什么进行分类的，要搞清楚，LTI系统是一个什么样的系统，以及卷积的操作，因果LTI等，回顾完这些之后，就开始了今天的学习。
首先是离散时间系统的描述，很有意思的一点，现在我们可以应用数学方法来描述离散时间系统了，常用的就是差分方程，至于差分方程有人说不会的，可以看高等数学或者是找找宇哥的课听。
一、递归\非递归的离散时间系统，
我也不多说了递归就是一个系统它在n时刻的输出
是依赖于一定数量的
，这样的系统就是递归的，相反的，非递归的就是仅仅依赖于当前和过去的输入
，我们用两个很简单的式子表示一下递归和非递归：
因果的实际可实现的递归：
![y(n)=F[y(n-1),y(n-2),\cdots,y(n-N),x(n),x(n-1),\cdots,x(n-M)]](http://img.e-com-net.com/image/info8/22be439d30844d119a27fcb7824e2c41.png){kind=small}
非递归：
![y(n)=F[x(n),x(n-1),\cdots,x(n-M)]](http://img.e-com-net.com/image/info8/24bc0674df244039b1d77ca4079803f6.png){kind=small}
我觉得清楚明白。
然后就到了差分方程推导这块，首先，我们得介绍两个概念：
对于一个信号来说，如果他是一个递归的系统，y可以表示成：
,
然后我们对他进行递归，计算
时候的连续值：
这样的话，我们就将一个系统响应分成了两个部分，一个是系统的初始条件，另一个是系统对输入信号的响应，
我们假设，
,也就是说，这个系统在时刻n=0初始时弛豫的，他的记忆为0。
1、零状态响应:
很简单吧，就是说这个系统零状态。
2、零输入响应（自然响应）：
这个就更简单了，x(n)=0嘛，就是我们的系统里面没有输入，这时候，
零输入响应是系统的本身的特性，零状态响应是输入信号给系统强加之后的响应，也常常被称为系统的强迫响应。从上面就得到，我们的系统可以表示成零输入响应和零状态响应的和。
然后，就是按照数学方法去求解差分方程，你要去计算一个齐次解
和一个特解
，然后二者相加，就是，和差分方程计算一样，如果我们想知道齐次解中的常系数{C}，就还得计算题目或者实际中得到的几个特殊值，这样才能够的到这些常系数，但是已经不难了，就是个带入特值求解嘛。
然后，有一个各种输入信号的特殊解的一般形式的表格，我觉得这个还是比较重要的，就写上吧：
输入信号 |
特殊解 |
| 常数A | K |
 |
 |
 |
 |
 |
 |
 |
 |
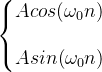然后我们来看到底什么样的系统可以是一个线性系统呢：
他必须满足的条件是什么？
书上给出了三个条件：
1、系统总是等于零输入响应和零状态响应之和
2、零状态响应满足叠加法则
3、零输入相应满足叠加法则
这样的系统就是一个线性系统。
上面的只是一个小插曲，有一个问题，一个可以用线性常系数差分方程表示的递归系统是LTI吗，答案是当然的，这是因为：系数全是常数，并不按时间特性去改变，所以，必然是LTI。
LTI 的冲激响应：
之前，上一篇博客里面对LTI的冲激响应被定义为系统对单位采样激励的相应
,在递归的情况下呢？
如果输入且系统是初始弛豫的，那么
仅是等于
系统对任何激励函数的全响应是由差分方程的两个结合和来组成的。
那么我们一个怎么样去对一个N解差分方程所描述的系统进行稳定性判断呢？
因为BIBO稳定要求冲激响应是绝对可加的，我们对于一个因果系统，就可以得到：
（lambda是特征多项式的根）这样子就能判断了：对于一个由线性常系数差分方程描述的因果IIR系统，其稳定的必要条件是特征多项式的所有根在幅度上小于1。
然后四LTI系统的实现，还记得数学信号处里5那一章中的那五个单位元件嘛？加法器，乘法器（常数、信号）、单位延迟、单位超前，一个系统，实际上就靠着这些个元件排列组合，以求实现相关功能。
我们举个例子：
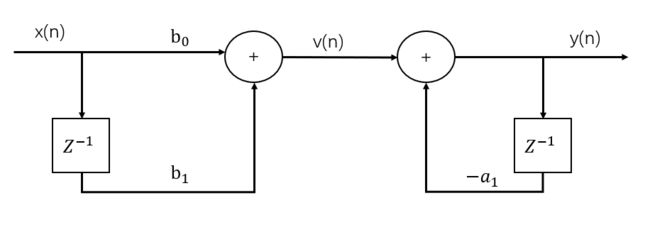
其实，我觉得这个跟电路图是很像的，上面这个例子，就可以这样子用元件来表示：
同时呢，我们也知道，交换级联的线性时不变系统的次序，整个系统的响应还是保持不变的，那么我们就可以把上面的给转换一下：
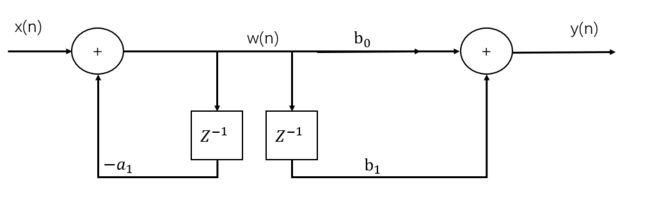
然后，你就发现，两个单位延迟元件可以合并：
那么这样子的话 ，我们就可以用上面从图一到图三的方式来推广到一个一般LTI系统：
如果我们用图一或者图二的方式，那么就需要N+M个延迟器和N+M+1个乘法器，用图三的话，只要N+M-1个乘法器和max{M,N}个延迟器，减少了硬件的使用量。
实际上，每个FIR系统可以通过非递归实现，但是从另一方面看，任何FIR系统又都是可以递归的实现的。这个书上又例子，我就不写了，我想其他的书上应该也是有的。
好了，前面哪些琐碎的概念的确写的难受，接下来要说的是一个非常重要的计算方法：相关，之前我就在昨天的卷积那里说到过相关，他和卷积的计算步骤很像的，但是，他却和卷积的意义是不一样的。
相关：计算两个信号的相关，其目的在于衡量两个信号的相似程度，并且由此来提取在很大程度上应用得到的信息。
主要要说的就是两个序列：自相关、互相关：
我们有两个实信号序列，且每个序列都是有限能量的：
，定义他们的互相关为：
或者
当然，你也可以用ryx来表示，只不过我们要求要遵守这样的规律：
也就是说这两个是偶对称序列，他们关于0对称。
计算互相关序列：平移一个序列，将两个序列相乘，再将成绩序列的所有值相加，如果我们有一段执行卷积的程序，就把x和y的反转序列作为输入，就可以计算互相关序列了：
注意，互相关是不可交换的运算，这是因为缺少了反转操作（不要看上面的这个式子，看定义式就明白了），一般来说，我们会把自、互相关给写成有限和的形式。
那么什么是自相关呢？
很简单，既让y=x不就行了，我们就这样简单的得到了自相关的定义：
或者
。
同时，如果说，我们的两个输入序列是长度为N的因果序列（
），那么我们就可以把自相关、互相关序列给表示成：
以及：
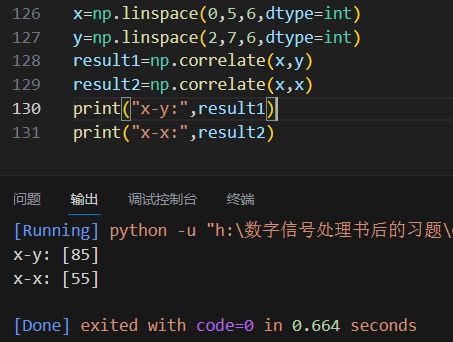
在计算的时候，python的numpy包的确是有相关的功能函数直接使用，很简单：
numpy.correlate(x, y, mode='valid', old_behavior=False)随便试了一下，还挺简单的：
那么，既然已经有了自相关、互相关的概念，我们就想知道，他们能干什么，或者说，他们有什么是我们可以用来帮助我们解决问题的性质？
1、信号的自相关序列再零延迟处得到器最大值，
2、我们可以对互相关运算中的信号进行缩放，这只会改变他的幅值大小，所以，在处理的时候，我们可以对一个互相关序列进行归一化而不改变其性质
3、自相关是偶函数，我们只要计算出一半就可以知道另一半了。
4、如果一个序列
是周期性的，那么其自相关序列也会有相同的周期（这一性质常被用来鉴别观测的物理信号的周期）。
5、系统输入和输出之间的互相关就是冲激响应和输入序列自相关之间的卷积：
6、输出信号的自相关：
emm，第二章我大致上就先了解到这个程度了，至于后面的，如果这两天做题过程中出现问题的话，我会补充的。