区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测

区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测

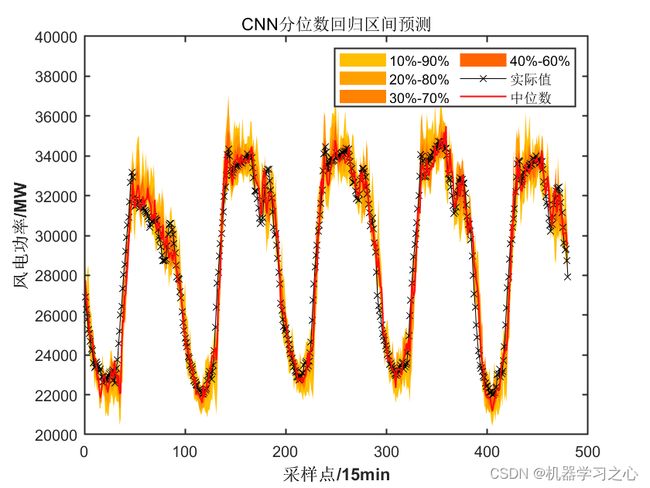
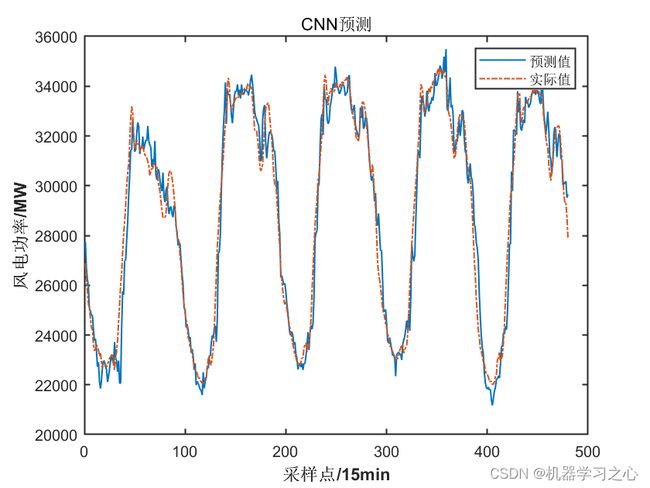
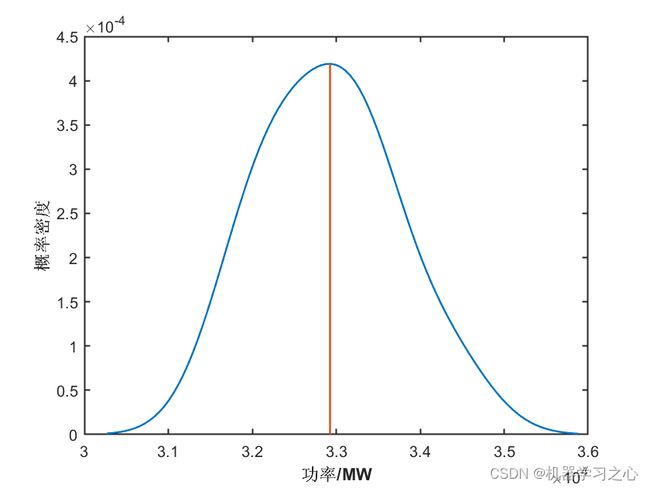
效果一览

基本介绍

区间预测 | MATLAB实现QRCNN卷积神经网络分位数回归时间序列区间预测
1.Matlab实现基于QRCNN分位数回归卷积神经网络的时间序列区间预测模型；
2.多图输出、多指标输出(MAE、RMSE、MSE、R2)，多输入单输出，含不同置信区间图、概率密度图；
3.data为数据集，功率数据集，用过去一段时间的变量，预测目标，目标为最后一列，也可适用于负荷预测、风速预测；MainQRCNNTS为主程序，其余为函数文件，无需运行；
4.代码质量高，注释清楚，含数据预处理部分，处理缺失值，如果为nan，用上一行替代，也含核密度估计。

模型描述

QRCNN是一种基于卷积神经网络（CNN）的分位数回归模型，用于时间序列区间预测。其全称为Quantile Regression Convolutional Neural Network。该模型可以用于预测时间序列数据的不同分位数，例如预测股票价格的上下限、风速的极值等。由于QRCNN采用卷积神经网络的结构，可以有效地捕捉时间序列数据的局部和全局特征，从而提高预测准确性。
QRCNN模型的主要思想是将时间序列数据分解成一系列窗口，并将每个窗口视为一个图像。然后，使用卷积神经网络对这些图像进行特征提取和分析，最终输出每个分位数的预测结果。QRCNN模型的训练过程采用分位数损失函数，以最小化所有分位数的预测误差。

QRCNN模型的优点包括：
能够有效地处理时间序列数据的不确定性和非线性特征；
能够同时预测多个分位数，从而提供更全面的预测结果；
可以灵活地处理不同长度的时间序列数据。
总之，QRCNN模型是一种用于时间序列区间预测的强大工具，可以帮助人们更好地理解和应用时间序列数据。
QRCNN模型的公式包括输入层、卷积层、池化层、全连接层和输出层。以下是QRCNN模型的主要公式：

输入层：
假设时间序列数据为$x_t$，则输入层将每个时间步$t$的数据作为一个输入节点$x_t$。
卷积层：
假设第$k$个卷积核的大小为$d_k$，则第$k$个卷积层的输出$z_k$可以表示为：

$$z_k=\sigma (W_k\ast x+b_k)$$

其中，$W_k$是第$k$个卷积核的权重矩阵，$\ast$表示卷积操作，$b_k$是偏置项，$\sigma$是激活函数，通常使用ReLU或tanh函数。
池化层：
假设第$k$个池化操作的大小为$m_k$，则第$k$个池化层的输出$y_k$可以表示为：

$$y_k=maxpool(z_k)$$

其中，$maxpool$表示最大池化操作。
全连接层：
假设第$l$个全连接层的输出为$h_l$，则第$l$个全连接层的输出$h_l$可以表示为：

$$h_l=\sigma (W_l\ast h_{l-1}+b_l)$$

其中，$W_l$是第$l$个全连接层的权重矩阵，$b_l$是偏置项，$\sigma$是激活函数。
输出层：
假设要预测$q$个分位数，第$q$个分位数为${\tau }_q$，则输出层的输出$y_q$可以表示为：

$$y_q=F_{{\tau }_q}(h_L)$$

其中，$F_{{\tau }_q}(h_L)$表示第$L$层的输出$h_L$在分位数${\tau }_q$处的累积分布函数（CDF）。
损失函数：
QRCNN模型采用分位数损失函数，定义为：

$$L_{\tau }(y,\hat{y})=(1-\tau )|y-\hat{y}|(y\le \hat{y})+\tau |y-\hat{y}|(y>\hat{y})$$

其中，$y$表示实际值，$\hat{y}$表示预测值，$\tau$表示分位数，$|\cdot {|}_{(\cdot )}$表示指示函数。
最终，QRCNN模型的目标是最小化所有分位数的预测误差的总和，即：

$$min\sum _{i=1}^n\sum _{q=1}^Q{L}_{{\tau }_q}(y_i,\widehat{y_i})$$

其中，$n$表示样本数量，$Q$表示分位数个数。

程序设计

• 完整程序和数据获取方式：私信博主。

% Divide the data into training and validation data sets
numTrainFiles = 90;
[imdsTrain,imdsValidation] = splitEachLabel(imds,numTrainFiles,'randomize');
% Define the convolutional neural network architecture.
layers = [
% Image Input Layer An imageInputLayer 
    imageInputLayer([64 64 1])
% Convolutional Layer 
convolution2dLayer(3,8,'Padding','same')
% Batch Normalization 
    batchNormalizationLayer
% ReLU Layer The batch
    reluLayer
% Max Pooling Layer  
    % More values means less weights
    maxPooling2dLayer(4,'Stride',4)
    %------------------------------
    convolution2dLayer(3,8,'Padding','same')
    batchNormalizationLayer
    reluLayer
    maxPooling2dLayer(5,'Stride',5)
    convolution2dLayer(3,8,'Padding','same')
    batchNormalizationLayer
    reluLayer
% Fully Connected Layer (Number of Classes) 
    fullyConnectedLayer(8)
% Softmax Layer 
    softmaxLayer
% Classification Layer The final layer 
    classificationLayer];
% Specify the training options
options = trainingOptions('sgdm', ...
    'InitialLearnRate',0.001, ...
    'MaxEpochs',20, ...
    'Shuffle','every-epoch', ...
    'ValidationData',imdsValidation, ...
    'ValidationFrequency',8, ...
    'Verbose',false, ...
    'Plots','training-progress');
% Train the network 
[net,info]= trainNetwork(imdsTrain,layers,options);

% Converting Serial Network to an Object
netobj = net.saveobj;
% Extracting Fully Connected Layer's Weights To Evolve
FullConn=netobj.Layers(13, 1).Weights;
netbias=netobj.Layers(13, 1).Bias;

%% Data for Each Weight
sizefinal=size(FullConn);
sizefinal=sizefinal(1,1);
for i=1:sizefinal
Inputs=FullConn(i,:);
Targets=Inputs;
data.Inputs=Inputs;
data.Targets=Targets;
datam{i}=JustLoad(data);
end;

————————————————
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/128252426

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340