机器学习回归任务指标评价及Sklearn神经网络模型评价实践
机器学习回归模型评价是指对回归模型的性能进行评估,以便选择最佳的回归模型。其中,MAE、MSE、RMSE 用于衡量模型预测值与真实值之间的误差大小,R² 用于衡量模型对数据的拟合程度。在实际应用中,我们可以使用这些指标来评估回归模型的性能,并对模型进行优化。
例如,在工业领域,回归算法可以通过对历史数据的回归分析,预测用电负荷、发电量等生产指标。
1. 机器学习回归模型的预测结果评价
机器学习回归模型的预测结果评价有很多方法,以下是一些常用的方法:
R2(决定系数):R2评估模型对数据的拟合程度,它的取值范围为0到1,越接近1表示模型的拟合程度越好(sklearn回归模型评估所使用的score默认是R2的计算公式)。R2的计算公式如下:
R 2 = 1 − ∑ i = 1 n ( y i − y i ^ ) 2 ∑ i = 1 n ( y i − y i ˉ ) 2 R2=1−\frac{\sum_{i=1}^{n}(y_i−\hat{y_i})^2}{\sum_{i=1}^n(y_i−\bar{y_i})^2} R2=1−∑i=1n(yi−yiˉ)2∑i=1n(yi−yi^)2
R2(决定系数)回归评分函数的最好分数是1.0,它可以是负数(因为模型可以任意变差)。
平均绝对误差(Mean Absolute Error,MAE):MAE是预测值与真实值之间差的绝对值的平均数,它的值越小表示模型预测的准确度越高。计算公式为:
M A E = 1 n ∑ i = 1 n ∣ y i − y i ^ ∣ MAE=\frac{1}{n}\sum_{i=1}^n∣y_i−\hat{y_i}∣ MAE=n1i=1∑n∣yi−yi^∣
又称L1范数损失,来衡量预测值与真实值之间的真实距离。
均方误差(Mean Squared Error,MSE):MSE是预测值与真实值之间差的平方的平均数,它的值越小表示模型预测的准确度越高。计算公式为:
M S E = 1 n ∑ i = 1 n ( y i − y i ^ ) 2 MSE=\frac{1}{n}\sum_{i=1}^n(y_i−\hat{y_i})^2 MSE=n1i=1∑n(yi−yi^)2
通过平方的形式便于求导,所以常被用作线性回归的损失函数。
均方根误差(Root Mean Squared Error,RMSE):RMSE是MSE的平方根,它的值越小表示模型预测的准确度越高。计算公式为:
R M S E = 1 n ∑ i = 1 n ( y i − y i ^ ) 2 RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i−\hat{y_i})^2} RMSE=n1i=1∑n(yi−yi^)2
常用来作为机器学习模型预测结果衡量的标准,衡量观测值与真实值之间的偏差。受异常点影响较大,鲁棒性比较差。
其中, y i y_i yi是真实值, y i ^ \hat{y_i} yi^是预测值, y i ˉ \bar{y_i} yiˉ是真实值的平均值,n 表示样本数量。
R平方(R-squared):R平方与R2的计算方式类似,但它可以对模型的复杂度进行惩罚,避免模型过拟合。
可决系数(Adjusted R-squared):可决系数是R平方的改进版本,它考虑了自变量数量对模型的影响,可以更准确地评估模型的拟合程度。
2. 如何评价机器学习回归模型
评价机器学习得到的回归模型可以从多个方面入手,例如:模型的拟合程度、模型的预测能力、模型的稳定性等。
其中,模型的拟合程度可以通过决定系数(Coefficient of Determination,R2)来衡量。R2的取值范围在0到1之间,越接近1表示模型对数据的拟合程度越好。但是,R2并不能告诉我们哪些变量对目标变量有影响。
模型的预测能力可以通过均方根误差(Root Mean Squared Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)等指标来衡量。这些指标可以用来衡量模型对新数据的预测能力。
模型的稳定性可以通过交叉验证(Cross Validation)等方法来衡量。交叉验证可以用来评估模型在不同数据集上的表现,从而判断模型是否过拟合或欠拟合。
3. Sklearn回归模型实践
3.1. 多层感知机回归模型
实践案例使用简洁的神经网络感知机(MLPRegressor)。
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.utils import column_or_1d
import pandas as pd
import numpy as np
import joblib
import matplotlib.pyplot as plt
df = pd.read_csv('power_pv09.csv')
# 数据处理过程,略
train_datas = df[cols_dict].loc[df['p_mp'] > 0]
y = train_datas[['ThisPower']]
X = train_datas.drop(columns='ThisPower')
model_filename = 'mlpmodel.joblib'
x_train, x_test, Y_train, Y_test = train_test_split(X, y, test_size=0.2)
std_x = StandardScaler()
std_x.fit(x_train)
# y值可以不进行归一化,使用原值
std_y = StandardScaler()
std_y.fit(Y_train)
y_train = std_y.transform(Y_train)
y_test = std_y.transform(Y_test)
X_train = std_x.transform(x_train)
X_test = std_x.transform(x_test)
forest_model = MLPRegressor(hidden_layer_sizes=(80, 90, 80),
solver = 'adam',
tol=1e-3, max_iter=600, random_state=0).fit(X_train, y_train)
joblib.dump(forest_model, model_filename) # 存储模型
y_ = forest_model.predict(X_test)
y_ = y_.reshape(-1,1)
pre_y = std_y.inverse_transform(y_)
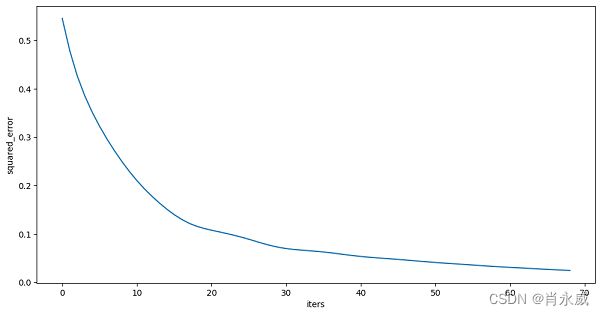
3.2. 可视化训练过程
# 可视化损失函数
plt.figure(figsize=(12,6))
plt.plot(forest_model.loss_curve_)
plt.xlabel("iters")
plt.ylabel(forest_model.loss)
plt.show()
注意:适用于solver = 'adam’等,牛顿法不适用solver=‘lbfgs’。
3.3. 回归模型评估
使用常用机器学习回归模型评估方法R2、MSE、MAE等方法,在Sklearn库中,分别调用其函数实现评估,具体函数详见如下代码。
R2 = forest_model.score(X_test, y_test)
print ("Test R2 Score = ", R2)
'''计算训练集 MSE'''
pre_train = forest_model.predict(X_train)
mse_train = mean_squared_error(pre_train,y_train)
print ("Train mean squared ERROR = ", mse_train)
'''计算训练集 MAE'''
pre_train = forest_model.predict(X_train)
mae_train = mean_absolute_error(pre_train,y_train)
print ("Train mean absolute ERROR = ", mae_train)
'''计算测试集mse'''
pred_test = forest_model.predict(X_test)
mse_test = mean_squared_error(pred_test,y_test)
print ("Test mean_squared ERROR = ", mse_test)
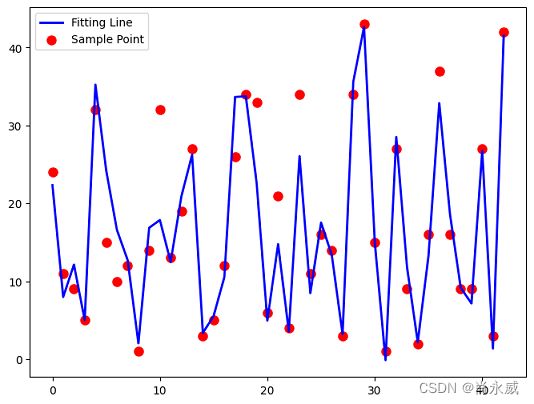
'''结果可视化'''
xx=range(0,len(y_test))
plt.figure(figsize=(8,6))
plt.scatter(xx,Y_test,color="red",label="Sample Point",linewidth=3)
plt.plot(xx,column_or_1d(pre_y, warn=True),color="blue",label="Fitting Line",linewidth=2)
plt.legend()
评估结果如下:
Test R2 Score = 0.884
Train mean squared ERROR = 0.0475
Train mean absolute ERROR = 0.147
Test mean_squared ERROR = = 0.1026
参考:
大鱼. 机器学习常见评价指标. 知乎. 2022.11
Xiaofei@IDO. 机器学习:回归模型的评价指标. CSDN博客. 2021.06