【鲁棒、状态估计】用于电力系统动态状态估计的鲁棒迭代扩展卡尔曼滤波器研究（Matlab代码实现）

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

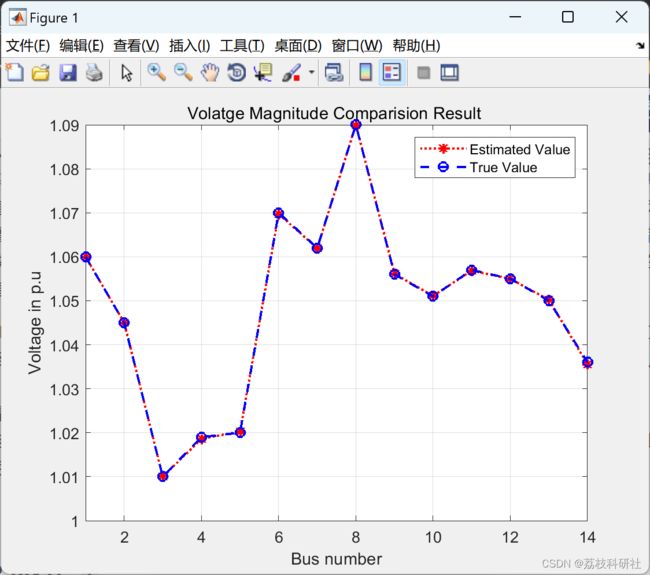
2.1 IEEE14节点

 ​

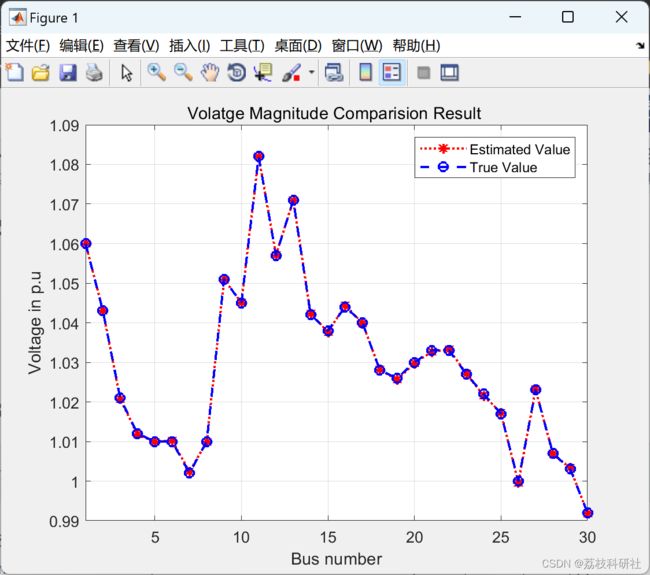
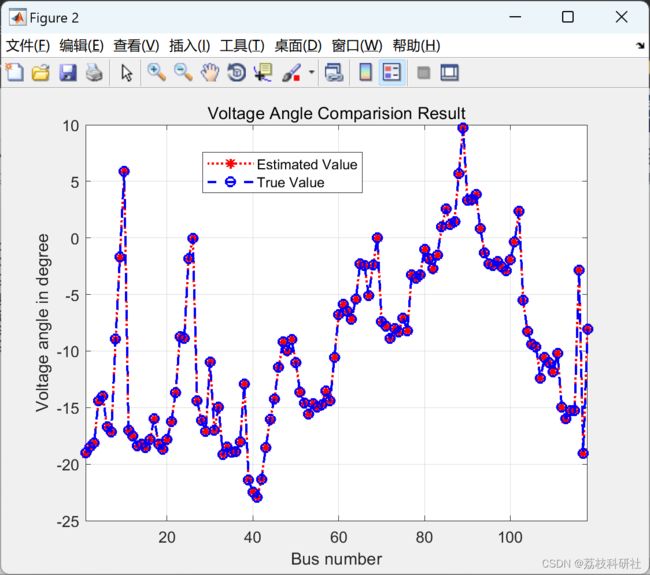
2.2 IEEE30节点

 ​

2.3 IEEE118节点

3 参考文献

4 Matlab代码、数据、文章讲解

---

​

1 概述

文献来源：

  

摘要：本文开发了一种基于广义最大似然法（称为GM-IEKF）的鲁棒迭代扩展卡尔曼滤波（EKF），用于估计电力系统在受到干扰时的状态动态。所提出的GM-IEKF动态状态估计器能够比传统的EKF和无迹卡尔曼滤波器（UKF）更快、更可靠地跟踪系统瞬变，这要归功于其批处理模式回归形式以及对创新和观测异常值的鲁棒性，即使在杠杆位置也是如此。创新异常值可能是由动态状态模型中的脉冲噪声引起的，而观测异常值可能是由于较大的偏差、网络攻击或PMU的通信链路暂时丢失引起的。通过最小化标准化残差的Huber凸成本函数，实现了高斯噪声下的良好鲁棒性和较高的统计效率。后者通过预测状态和创新向量的两个时间序列的鲁棒距离的函数进行加权，并通过投影统计量进行计算。使用总影响函数推导状态估计误差协方差矩阵，从而在下一个时间步长中产生鲁棒状态预测。在IEEE 39节点测试系统上进行的仿真结果表明，GM-IEKF在高斯和非高斯过程和观测噪声下具有良好的性能。

原文摘要：

Abstract:

This paper develops a robust iterated extended Kalman filter (EKF) based on the generalized maximum likelihood approach (termed GM-IEKF) for estimating power system state dynamics when subjected to disturbances. The proposed GM-IEKF dynamic state estimator is able to track system transients in a faster and more reliable way than the conventional EKF and the unscented Kalman filter (UKF) thanks to its batch-mode regression form and its robustness to innovation and observation outliers, even in position of leverage. Innovation outliers may be caused by impulsive noise in the dynamic state model while observation outliers may be due to large biases, cyber attacks, or temporary loss of communication links of PMUs. Good robustness and high statistical efficiency under Gaussian noise are achieved via the minimization of the Huber convex cost function of the standardized residuals. The latter is weighted via a function of robust distances of the two-time sequence of the predicted state and innovation vectors and calculated by means of the projection statistics. The state estimation error covariance matrix is derived using the total influence function, resulting in a robust state prediction in the next time step. Simulation results carried out on the IEEE 39-bus test system demonstrate the good performance of the GM-IEKF under Gaussian and non-Gaussian process and observation noise.

随着广域同步相量测量的广泛部署，人们提出了新技术 通过动态状态估计器 （DSE） 有效跟踪电力系统动态 [1]–[3]。通过使用估计的系统动态 状态，可以实现改进的实时控制方案，例如通过对 FACTS 设备和 广域电力系统稳定器，仅举几例，从而增强电力系统的稳定性。

为了跟踪受到较大干扰的电力系统动态，扩展卡尔曼滤波器（EKF）和无味滤波器 卡尔曼滤波器（UKF）最近被提出。例如，黄等人。 [3] 和方和韦贝 [4] 进行了调查 使用卡尔曼滤波技术采用PMU数据进行实时状态和参数估计的好处。 在他们的工作之后，Ghahremani和Kamwa[5]提出了一个基于EKF的修改。 DSE用于应对由于无刷励磁系统而无法计量现场电压的情况。这 后来随着去中心化DSE的开发，工作得到了扩展，同时放宽了对已知DSE的假设 机械扭矩 [6]。

为了规避 EKF 的一阶逼近误差，在 模型，迭代的 EKF （IEKF） [4] 和 UKF 被提议为 替代方法。具体来说，IEKF对系统非线性方程进行线性化迭代，以补偿 高阶项，而 UKF 通过确定性地提供 sigma 来利用无迹变换 点近似随机状态向量的均值和协方差矩阵，从而获得比 EKF [7]， [8]。基于 UKF 的 DSE，使用 在 [9] 中提出了四阶生成器模型来估计 单机无限总线电源系统。同样，在[10]中为多机系统开发了集中式UKF，而分散式策略则没有 [11]中提倡要求传输本地信号，显着 提高计算效率。然而，[12] 已经证明，在存在观测异常值的情况下，EKF 或 UKF 的性能会大大降低，原因是 他们缺乏稳健性。为了缓解这个问题，[11] 中提倡基于规范化创新向量的测试来检测观测异常值，尽管该测试在 创新异常值。在[13]中，鲁哈尼和阿布尔开发了一个分布式 基于UKF的两阶段鲁棒DSE，使用最小绝对值（LAV）估计器，可以处理观测异常值 PMU 测量。然而，作者没有解决动态状态估计器对创新的脆弱性。 由状态预测模型中的近似值或脉冲系统过程噪声引起的异常值。

Gandhi和Mili[14]提出了一个用于线性动力学的鲁棒卡尔曼滤波器 型。在本文中，我们将这项工作扩展到了一般非线性动态状态估计问题，其中有几个 新功能。后者包括派生新的批处理模式回归形式，以增强数据冗余，即 基于投影统计的新型异常值检测方法，并应用于预测的两个时序和 创新向量，以及所提出的鲁棒广义最大似然的鲁棒状态协方差矩阵 迭代的 EKF （GM-IEKF） 方法。这些功能使我们的GM-IEKF能够更可靠、更可靠地跟踪电力系统动态 比传统的EKF更快，即使在存在观察和创新异常值或非高斯PMU噪声的情况下也是如此。 

2 运行结果

2.1 IEEE14节点

  

  

  

2.2 IEEE30节点

  

  

  

2.3 IEEE118节点

  

  

  

 部分代码：

%displayout(E,'a'); % Displaying output in tabular form
f = E(nbus+1:end);
e = E(1:nbus);
v=e+1i*f;
V=abs(v);
Del=round(angle(v)*180/pi*100)/100;
disp('-------- State Estimation ------------------');
disp('--------------------------');
disp('| Bus |    V   |  Angle  | ');
disp('| No  |   pu   |  Degree | ');
disp('--------------------------');
for m = 1:nbus
    fprintf('%4g', m); fprintf('  %8.4f', V(m)); fprintf('   %8.4f', Del(m)); fprintf('\n');
end
disp('---------------------------------------------');
%% calculate the estimated value
%Measurement Function, h
h1 = V(fbus (ei),1);  %voltage measurement
h2 = Del(fbus (fi),1);  %angle measurement
h3 = zeros(npi,1);  %real power injection
h4 = zeros(nqi,1);  %reactive power injection
h5 = zeros(npf,1);  %real power flow
h6 = zeros(nqf,1);  %reactive power flow
%Measurement function of power injection
for i = 1:npi
m = fbus(ppi(i));
for k = 1:nbus
% Real injection
h3(i)=h3(i)+(G(m,k)*(e(m)*e(k)+f(m)*f(k))+B(m,k)*(f(m)*e(k)-e(m)*f(k)));
% Reactive injection 
h4(i)=h4(i)+(G(m,k)*(f(m)*e(k)-e(m)*f(k))-B(m,k)*(e(m)*e(k)+f(m)*f(k)));
end
end
%Measurement function of power flow
for i = 1:npf
    m = fbus(pf(i));
    n = tbus(pf(i));
% Real injection
h5(i) =(e(m)^2 + f(m)^2)*g(m,n)-(g(m,n)*(e(m)*e(n)+f(m)*f(n))+b(m,n)*(f(m)*e(n)-e(m)*f(n)));
% Reactive injection 
h6(i) =-g(m,n)*(f(m)*e(n)-e(m)*f(n))+b(m,n)*(e(m)*e(n)+f(m)*f(n))-(e(m)^2 + f(m)^2)*(b(m,n)+bsh(m,n));
end
%% note that the angle measurement should be converted to radians for measurement comparison
h = [h1; h2; h3; h4; h5; h6];
%% % the estimated voltage and the true voltage magnitude in p.u.
figure(1) 
K=1:1:nbus;
[Vtrue Angletrue]=IEEE_true_value(nbus); % true voltage magnitude
plot(K,V,'r:*',K,Vtrue,'b--o','linewidth',1.5)
title('Volatge Magnitude Comparision Result ')
xlabel('Bus number')
xlim([1 nbus])
ylabel('Voltage in p.u')
legend('Estimated Value','True Value')
grid on
% % the estimated voltage angle and the true voltage angle in degree
figure(2)
j=1:1:nbus;
plot(j,Del,'r:*',j,Angletrue,'b--o','linewidth',1.5)
title('Voltage Angle Comparision Result')
xlabel('Bus number')
xlim([1 nbus])
ylabel('Voltage angle in degree')
legend('Estimated Value','True Value')
grid on
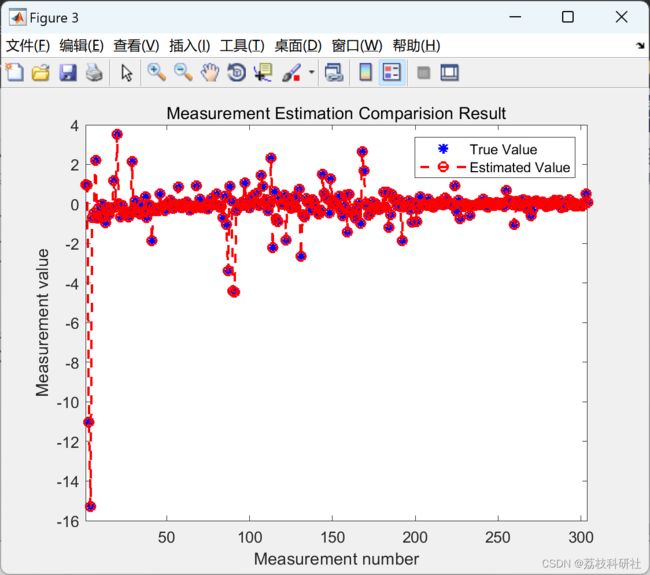
%% % the estimated and true measurement in degree
figure(3)
i=1:1:length(z);
estimated_measurement=plot(i,Z,'b*',i,h,'r--o');
set(estimated_measurement(1),'linewidth',1.5);
set(estimated_measurement(2),'linewidth',1.5);
title('Measurement Estimation Comparision Result')
xlabel('Measurement number')
xlim([1 length(z)])
ylabel('Measurement value')
legend('True Value','Estimated Value')
%% % the estimated and true measurement in degree
figure(3)
i=1:1:length(z);
estimated_measurement=plot(i,Z,'b*',i,h,'r--o');
set(estimated_measurement(1),'linewidth',1.5);
set(estimated_measurement(2),'linewidth',1.5);
title('Measurement Estimation Comparision Result')
xlabel('Measurement number')
xlim([1 length(z)])
ylabel('Measurement value')
legend('True Value','Estimated Value')
for i=1:nbus
voltage_error(i)=norm((Vtrue(i)-V(i)),inf)./abs(Vtrue(i));
angle_error(i)=norm((Angletrue(i)-Del(i)),inf)./abs(Angletrue(i));
end
Max_voltage_estimation_error=max(voltage_error)
Max_angle_estimation_error=max(angle_error)
Mean_voltage_estimation_error=mean(abs(Vtrue-V))
Mean_angle_estimation_error=mean(abs(Angletrue-Del))

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]J. Zhao, M. Netto and L. Mili, "A Robust Iterated Extended Kalman Filter for Power System Dynamic State Estimation," in IEEE Transactions on Power Systems, vol. 32, no. 4, pp. 3205-3216, July 2017, doi: 10.1109/TPWRS.2016.2628344.

4 Matlab代码、数据、文章讲解